2014年最新人教版八年级下一次函数单元检测B卷(带详细答案)
在同一直角坐标系内一次作出函数y=x+1,y=2x+1,y=3x+1的图象。
(1)这几个图象之间有什么差别,又有什么联系?
(2)一次函数y=kx+b的一次项系数k对函数的图象有什么影响?
(1)这几个图像都经过(0,1)点,且y都随x的增大而增大,但是这几个图像的倾斜程度不同。
(2)对图像倾斜度有影响!
已知函数 y=x²-4x+3。
(1)画出函数的图象;
(2)观察图象,当x取哪些值时,函数值为0?
已知函数f(x)=a2+k的图象经过点(1,7),且其反函数f-1(x)的图像经过点(4,0),则函数f(x)的表达式是 ( )
A.f(x)=4x+3
B.f(x)=2x+5
C.f(x)=5x+2
D.f(x)=3x+5
已知m是整数,且一次函数y=(m+4)x+m+2的图象不过第二象限,则m= ;
-3或-2
已知一次函数的图象经过点A(2,1),B(-1,-3)
(1)求此一次函数的解析式;
(2)求此一次函数的图象与x轴、y轴的交点坐标;
(3)求此一次函数的图象与两坐标轴所围成的三角形面积。
(1)y=![]() x -
x - ![]()
(2)与x轴的交点坐标(![]() ,0);与y轴的交点坐标(0,-
,0);与y轴的交点坐标(0,- ![]() )
)
(3)面积为![]()
一次函数单元检测 B 眼识金!1已知函数 y=kx+b 的图象如图,则 y=2kx+b 的图象可能是()、 、 、 、2已知一次函数 y=(x+k+1 的图象不过第三象限,则 k 的取值范围是()、k 2、k 2、- 1 k 2、- 1 k 23如图,直线 y=kx+b 交坐标轴于 A,B 两点,则不等式 kx+b0 的解集是()、x 、x 3、x 、x 34已知直线的方程式为 ax+by+c=0,且 a0cb,则方程式的图象为()、 、 、 、5在平面直角坐标系内,直线 y= x+3 与两坐标轴交于 A、B 两点,点 O 为坐标原点,若在该坐标平面内有以点34P(不与点 A、B、O 重合)为顶点的直角三角形与 等,且这个以点 P 为顶点的直角三角形与 一条公共边,则所有符合条件的 P 点个数为()、9 个 、7 个 、5 个 、3 个6如图,点 A 的坐标为(),点 B 在直线 y=x 上运动,当线段 短时,点 B 的坐标为()、( 0, 0) 、 、 、2-( , ) 1, ) 2-( , )7根据生物学研究结果,青春期男女生身高增长速度呈现如下图规律,由图可以判断,下列说法错误的是()、男 生 在 13 岁 时 身 高 增 长 速 度 最 快 、女 生 在 10 岁 以 后 身 高 增 长 速 度 放 慢 、1 1 岁 时 男 女 生 身 高 增 长 速 度 基 本 相 同 、女 生 身 高 增 长 的 速 度 总 比 男 生 慢8汽车开始行驶时,油箱内有油 40 升,如果每小时耗油 5 升,则油箱内余油量 Q(升)与行驶时间 t(时)的函数关系用图象表示应为()、 、 、 、9已知一次函数的图象与直线 y= 平行,且过点(8,2),那么此一次函数的解析式为()、y =、y =-x

B.函数f(x)在定义域范围内,y随着x的增大而减小
C.若点C(-1,m),点B(2,n),在函数f(x)的图象上,则m<n
D.函数f(x)图象对称轴的直线方程是y=x
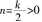
m<n,C正确;函数f(x)图象对称轴有两条,y=x和y=-x,D错误。
(1)求k的取值范围;
(2)若|x1-x2|=x1x2-1,求k的值。
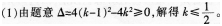
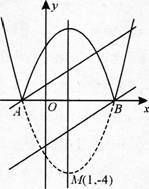
(2)由方程有x1+x2=2(k-1),x1x2=k2。若x1-x2=x1x2-1,贝4(x1+x2)2-4x1x2=x1x2-1)2,即4(k-1)2-4k2=(k2-1)2,即(k2-2k+3)(k2+2k-1)=0,解得
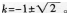
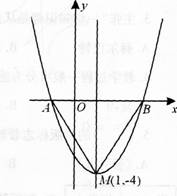
(1)求出图象与戈轴的交点A,B的坐标;
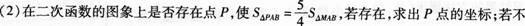
存在,请说明理由;
° (3)将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b的取值范围.
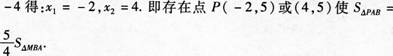
(3)如图,当直线Y=x+b经过A(-1,0)时-1+b=0,
可得b=1,又因为b<1,
故可知Y=x+b在Y=x+1的下方,
当直线Y=x+b经过点B(3,0)时,3+b=0,则b=-3,
由图可知,b的取值范围为-3<b<1时,
直线Y=x+b(b<1)与此图象有两个公共点.
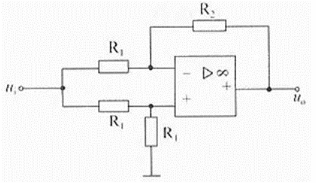
B.-1.5V
C.-0.5V
D.0.5V
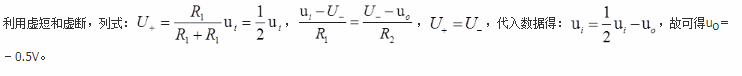
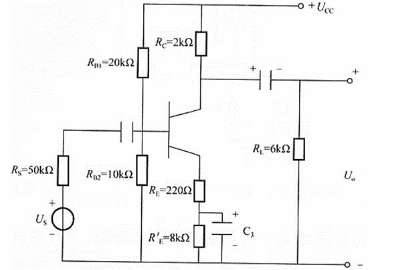
B.Au=6.5,ri=5.2Ω,ro=20kΩ
C.Au=-65,ri=1kΩ,ro=6kΩ
D.Au=65,ri=200Ω,ro=2kΩ

故晶体管的放大倍数
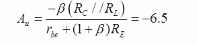
输入电阻ri=RB1//RB2//[rbe+(1+β)RE]=20//10//23.22≈5.18kΩ。
输出电阻ro≈RC=2kΩ。

