初二数学下学期期中模拟考试
小玲是初二年级的学生。她在2011学年的期中考试中,估计自己的数学成绩为85分,可实际最终考试成绩为90分。于是,她将期末数学考试的理想成绩定为95分。根据阿尔德弗尔的ERG理论,这反映了小玲的( )。
A.认知需要
B.求知需要
C.成长需要
D.关系需要
阿尔德弗尔的ERG理论中,E是生存的需要,这类需要关系到人的机体的存在或生存。R是关系的需要,是指发展人际关系的需要。G是成长的需要,是个人自我发展和自我完善的需要。由题干可知,小玲通过不断学习希望自己能够不断提高,所以正确答案是C。
列不等式(组):
(1)x+1是负数;
(2)x²是非负数;
(3)x的2倍与3的差小于0;
(4)a的5倍与3的差不小于10,且不大于20。
![]() (1)x+1<0
(1)x+1<0
(2)x20
(3)2x-3<0
(4)20>5a-310
用适当的符号表示下列关系:
(1)x的3倍与8的和比x的5倍大;
(2)x²是非负数;
(3)地球上海洋的面积大于陆地面积;
(4)老师的年龄比你的年龄的2倍还大;
(5)铅球的质量比篮球的大。
(1)3x+8>5x (2)x²0
(3)S1>S2(S1代表海洋面积,S2代表陆地面积)
(4)x>2y(x表示老师的年龄,y表示你的年龄)
(5)m1>m2(m1代表铅球的质量,m2代表篮球的质量)
某考试均为判断题,共10题,每题10分,满分为100分。考生答题时认为正确则画为“O”.认为不正确则画 “X” 。以下是考生的答题情况以及甲、乙、丙的实际得分,则丁的得分为 。
题号 1 2 3 4 5 6 7 8 9 10 得分
甲 X X O X O X X O X X 70分
乙 X O O O X O X O O O 50分
丙 X O O O X X X O X O 30分
丁 X X O O O X X O O O ? 分
A. 20分
B. 40分
C. 60分
D. 80分
7.【答案】c。解析:首先观察甲和丙,得分相差40分.而他们的答案不一样的也恰好有4题,那么也就是说,丙和甲不一样的题(即2,4,5,10)甲都做对了,而这四道题恰好乙也全做错了,而乙一共做错了5道题,也就说剩下的题目(1,3,6,7,8,9)中,只有乙只错一个;又四人判断一致的题目(即1,3,7,8)中必有一个四个人全做错了,因为丙一共只做对3道题,那么,也就是说6,9题乙做对了,那么现在答案除了l,3,7,8,都确定了,即(2,4,5,10)与甲一致,(6,9)与乙一致,在这6道题中丁做对了3道,剩下的(1,3,7,8)又丁做对3道,综上所述,丁得分60分。
B. 5
C. 6
D. 7
初二数学下学期期中模拟考试初二数学下学期期中模拟考试(考试时刻:120 分钟,满分 100 分)题号得分一二三四总分一、填空题(每题 2 分,共 26 分)1、用适当的符号表示下列关系:x的2x的3倍与7的差是非负数;与5的差不小于1;32、已知 ab,用“”或“”号填空:a 3b3;4a4b;x24x243、当 x时,分式的无意义;当 x时,分式值为零;x 2x 24、一件商品的进价是500元,标价为600元,打折销售后要保证获利不低于8%,则此商品最多打折;a2bcx212x 25、化简:,2,;abx 2x 11 x26、已知x y 6,xy 4,则x y xy的值为;7、多项式x kx 9是完全平方式,那么k;8、已知:ABCD,A、E、F 共线,B、C、F 共线,则与FCE 相似的三角形有;二、选择题(每题 3 分,共 18 分)222311x213xy111、在、a 中分式的个数有()2x yx2mA、2 个 B、3 个 C、4 个 D、5 个2、适合不等式5 x 5的整数为边长,能够构成一个()2A、等边三角形 B、等腰三角形 C、直角三角形 D、一样三角形3、下列从左到右的变形,是因式分解的是()A、a 3a 3 a 9 B、x x 5 xx 1522C、x 1 xx 2122 D、x 4x 4 x 2x24、关于任何整数m,多项式4m 59都能()A、被8整除 B、被m整除 C、被m1整除 D、被2m 1整除5、以下两个图形必定相似的是()A、有两条边对应成比例的等腰三角形 B、有一角是25的等腰三角形C、有一个角是100的等腰三角形 D、有一个角相等,两边成比例的三角形6、下列各式中,一定成立的是()A、oob a2 1 B、a b a2b2a bx y1222a 2ab b b a D、2xy x2 y2x yC、三、解答题(共 37 分)1、求下列不等式(组),并将解集表示在数轴上(1 题 3 分、2 题 4 分,共 7 分)5x 1 3(x 1)3 2x2x 1(1)、(2)、2x 15x 1231232、分解因式(每题 3 分,共 6 分)(1)、x y 2xy y(2)、xx y yy x2233、利用分解因式进行简便运算(每题3 分,共 6 分)(1)、18.91313132222、6.63.437.1(2)5555554、化简(每题 3 分,共 6 分)(1)、a ba baba5、先化简,再求值(4 分)a 1a2 4a 4a2 42a 2,其中a 1。6、解方程:(每题 4 分,共 8 分)(1)、x2x 565 2x12yy y22)、9y 3y 3y(2)、3x 1x 2xx 1 0(四、运用题(1、2 题各 6 分,3 题 7 分,共 19 分)1、有一群猴子,一天结伴去偷桃子,在分桃子时,假如每个猴子分了3 个,那么还剩 59个;假如每一个猴子分5 个,都能分得桃子,但剩下一个猴子分得的桃子不够5 个,你能求出有几只猴子,几个桃子吗?2、某中学到离学校 15 千米的西山春游,先遣队与大队同时动身,行进速度是大队的1.2倍,以便提早3、一项工程,需要在规定日期内完成,假如甲队独做,恰好如期完成,假如乙队独做,就要超过规定 3 天,现在由甲、乙两队合作2 天,剩下的由乙队独做,也刚好在规定日期内完成,问规定日期是几天?1小时到达目的地做预备工作,求先遣队与大队的速度各是多少?2

已知,得分至少为3分的,人均2x分;得分最多为7分的,人均x分。这个班级总人数是:

第二步,设得分至少为3分的人数为y,则全班总分数=2x×y+2×5+1×3=2xy+13①;得分至少为7分的人数为y+5+3+8-2-2-4=y+8,则全班总分数=(y+8)×x+2×10+2×9+4×8=xy+8x+70②。根据①=②,化简可得xy=8x+57,则

因此,选择A选项。

已知,得分至少为3分的,人均2x分;得分最多为7分的,人均x分。这个班级总人数是:
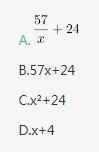
第二步,设得分至少为3分的人数为y,则全班总分数=2x×y+2×5+1×3=2xy+13①;得分最多为7分的人数为y+5+3+8-2-2-4=y+8,则全班总分数=(y+8)×x+2×10+2×9+4×8=xy+8x+70②。根据①=②,化简可得xy=8x+57,则

因此,选择A选项。

已知,得分至少为3分的,人均2x分;得分最多为7分的,人均x分。这个班级总人数是:
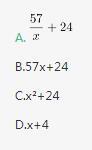
第二步,设得分至少为3分的人数为y,则全班总分数=2x×y+2×5+1×3=2xy+13①;得分最多为7分的人数为y+5+3+8-2-2-4=y+8,则全班总分数=(y+8)×x+2×10+2×9+4×8=xy+8x+70②。根据①=②,化简可得xy=8x+57,则

因此,选择A选项。
B. 40分
C. 60分
D. 80分
B. 5
C. 6
D. 7
