单选题有甲、乙、丙、丁4人参加期末考试，考试的科目是语文、数学和自然（每一门科目的满分不一定相同）。已知甲语文得40分，数学和自然得满分，平均分为50分；乙数学得57分，语文和自然为满分，平均分为59分；丙自然得17分，语文和数学为满分，平均分为49分；丁的成绩最好，语文、数学和自然都是满分，那么丁的平均分为多少？A 60分B 65分C 70分D 75分

题目
单选题
有甲、乙、丙、丁4人参加期末考试，考试的科目是语文、数学和自然（每一门科目的满分不一定相同）。已知甲语文得40分，数学和自然得满分，平均分为50分；乙数学得57分，语文和自然为满分，平均分为59分；丙自然得17分，语文和数学为满分，平均分为49分；丁的成绩最好，语文、数学和自然都是满分，那么丁的平均分为多少？
A

60分

B

65分

C

70分

D

75分

相似考题

1.小学毕业考核，语文、数学为考试学科，其他为__________科目。

2.有120名学生报考语文、数学、英语竞赛，已知现在有35人报考语文竞赛，45人报考数学竞赛，55人报考英语竞赛，其中30人同时报考了语文和数学竞赛，26人同时报考了语文和英语竞赛，38人同时报考了数学和英语竞赛，问至少还有多少人没有报考任何一科?A．0B．41C．53D．79

3.我想当小学科学老师，应该考哪科的教师资格？ 今年天津教师资格考试小学科目有：语文、数学、英语、信息技

4.在某次考试中．小明的语文、数学成绩均为80，英语成绩为75。已知全班三科平均成绩都为65，语文标准差为10，数学标准差为l5，英语标准差为5。小明三科的成绩按照标准分 由大到小进行排序的结果是A．语文、数学、英语 B．英语、数学、语文C．英语、语文、数学 D．语文、英语、数学

参考答案和解析
正确答案： C
解析：
更多“有甲、乙、丙、丁4人参加期末考试，考试的科目是语文、数学和自然（每一门科目的满分不一定相同）。已知甲语文得40分，数学和”相关问题

  • 第1题：

    教师申请参加《专业合格证书》的文化专业知识考试，需要参加哪几门课程的考试?()

    A.教育学和心理学基本原理

    B.语文和数学任选一门

    C.其他学科(自然、地理、政治、历史、音乐、美术、体育)任选一门

    D.教材与教法考试


    正确答案：AD

  • 第2题：

    有l20名学生报考语文、数学、英语竞赛，已知现在有35人报考语文竞赛，45人报考数学竞赛，55人报考英语竞赛，其中30人同时报考了语文和数学竞赛，26人同时报考了语文和英语竞赛，38人同时报考了数学和英语竞赛，问：至少还有多少人没有报考任何一科? A．0 B．41 C．53 D．79


    正确答案：C
    要使已经报名的人数尽量多，则三科都报的人尽量多，最多只能为26人。此时利用容斥原理可得，已经报名的人数为35+45+55-30-26-38+26＝67人，则至少还有120-67＝53人都没有报考任何一科。

  • 第3题：

    二、数学运算(共10题，每题0.5分。共5分。你可以在草稿纸上运算。要求你充分利用所给条件。寻找解决问题的捷径。)请开始答题：

    第 31 题 某班有40人，在期末考试中，语文有35人及格，数学有32人及格，语文有33人及格，不及格的人中没有只有一门不及格的，其中有2人全都不及格，有4人语文和数学都不及格，有6人数学和外语都不及格，有多少人语文和外语都不及格？（ ）

    A．2

    B．3

    C．4

    D．5


    正确答案：B
    (1)全班共40人。(2)设语文和外语都不及格的为x人。由于有4人语文和数学都不及格，减去2个都不及格的，有2个仅语文和数学不及格而外语及格，由于语文和外语都不及格的为。人，减去2个都不及格的为(x一2)个仅语文和外语不及格而数学及格的，即40＝35+2+(x一2)+2，解得X＝3，故选B。

  • 第4题：

    甲、乙、丙三人要装订语文和数学课本。装订语文课本的工作量比装订数学课本的工作量多1/4，甲、乙、丙三人单独完成数学课本的装订各需20天、24天和30天。为了共同完成这两项任务，先安排甲装订数学课本，乙、丙一起装订语文课本；经过几天后，又调丙去帮甲装订数学课本。最后两种课本的装订任务同时完成，那么乙、丙二人合作了（ ）天。

    A．12

    B．15

    C．17

    D．18


    正确答案：B
    取20，24，30的最小公倍数120，设装订数学课本的工作量为120，那么装订语文课本的工作量为(1+1/4)×120=150。那么甲、乙、丙每天完成的工作量分别是6，5，4。三人装订完两种课本共需要(120+150)÷(6+5+4)=18(天)。乙在这18天里，一直在装订语文课本，完成了18×5=90，剩下的装订语文课本的任务都由丙完成，需要(150-90)÷4=15(天)。所以乙和丙共合作了15天，答案为B。

  • 第5题：

    某班有40人，在期末考试中，语文有35人及格，数学有32人及格，外语有33人及格，不及格的人中没有只有一门不及格的，其中有2人全都不及格，有4人语文和数学都不及格，有6人数学和外语都不及格，有多少人语文和外语都不及格?（ ）

    A．2

    B．3

    C．4

    D．5


    正确答案：B
    (1)全班共40人。(2)设语文和外语都不及格的为X人。由于有4人语文和数学都不及格的减去2个都不及格的，有2个仅语文和数学不及格而外语及格，由于语文和外语都不及格的为％人，减去2个都不及格的为(x－2)个仅语文和外语不及格而数学及格的，全班共40人，即40=35+2+(x－2)+2，解得x=3，故选B。

  • 第6题：

    甲、乙和丙三人在某中学分别教语文、数学、英语、物理、化学和政治六门课程中的两门。已知：每门课程只由甲、乙、丙三人中的一人负责，数学老师和物理老师是邻居；甲是三人中年龄最小的；丙和语文老师、物理老师一起回家；语文老师比政治老师年龄要大；周末，英语老师，政治老师和甲一起打球。
    由此可知，三位老师所教的课程是：

    A.甲教物理和化学，乙教英语和语文，丙教数学和政治
    B.甲教数学和化学，乙教政治和语文，丙教物理和英语
    C.甲教物理和英语，乙教化学和数学，丙教语文和政治
    D.甲教英语和化学，乙教物理和语文，丙教数学和政治

    答案：A
    解析：
    第一步，确定题型。
    题干有明显的信息匹配特征，确定为分析推理。
    第二步，分析条件，进行推理。
    由“丙和语文老师、物理老师一起回家”可得丙不是语文、物理老师，排除B项和C项；
    由“周末，英语老师，政治老师和甲一起打球”可得甲不是英语、政治老师，排除D项。
    因此，选择A选项。

  • 第7题：

    “3+X”的高考科目设置中，语文、数学、外语3门是必考的，没有什么可以商量的，关键是如何选择“X”。上面的句子想表达的是：在“3+X”的高考科目设置中（）

    • A、X”是最关键的
    • B、语文、数学、外语是最重要的
    • C、语文、数学、外语不如“X”重要
    • D、X”和语文、数学、外语一样重要

    正确答案:D

  • 第8题：

    在教育改革中，（）实行社会化考试和一年多考。

    • A、语文
    • B、数学
    • C、语文和数学
    • D、英语

    正确答案:D

  • 第9题：

    单选题
    “甲：你上学期语文、数学考试成绩怎么样？乙：我语文考得不错，得了80多分呢？” 上面乙的回答违反了合作原则的（）。
    A

    数量准则

    B

    关联准则

    C

    质量准则

    D

    方式准则


    正确答案： B
    解析： 暂无解析

  • 第10题：

    单选题
    在某次考试中，小明的语文、数学成绩均为80，英语成绩为75。已知全班三科平均成绩都为65，语文标准差为10，数学标准差为15，英语标准差为5。小明三科的成绩按照标准分由大到小进行排序的结果是（　　）。
    A

    语文、数学、英语

    B

    英语、数学、语文

    C

    英语、语文、数学

    D

    语文、英语、数学


    正确答案： C
    解析： 暂无解析

  • 第11题：

    某中学115班共有48人，在课堂上完成语文、数学作业的情况有三种：一种做完语文作业没有做完数学作业，一种做完数学作业没有做完语文作业，一种语文、数学作业都做完了。已知做完语文作业的有37人，做完数学作业的有42人。问语文、数学作业都做完的有多少人?（ ）

    A．28人

    B．31人

    C．37人

    D．42人


    正确答案：B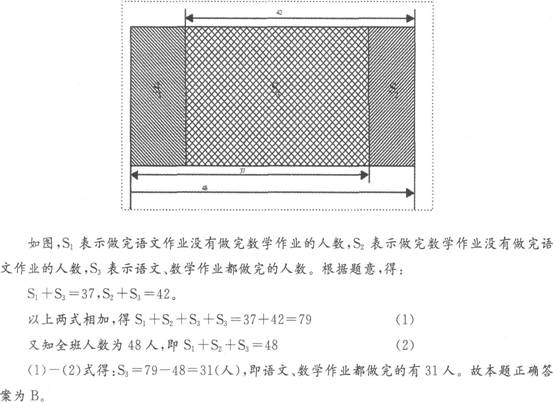

  • 第12题：

    .五年级一班有32人参加数学竞赛，有27人参加英语竞赛，有22人参加语文竞赛，其中参加了数学和英语两科的有12人，参加了语文和英语的有14人，参加了数学和语文两科的有10人，那么五年级一班至少有多少人?( )。

    A. 45    B. 47C. 55    D. 57


    至少：让尽量少的人参加3门竞赛  由题知 至少2人全参加(参加语文英语14人，参加数学和语文两科的有10人 10+14大于22 所以至少2人全参加） 10人只参加英语数学 12人只参加语文英语 8人只参加数学语文 
          32+27+22-14-12-10+2=47

  • 第13题：

    某校参加数学竞赛有120名男生、80名女生，参加语文竞赛有120名女生、80名男生。已知该校总共有260名学生参加了竞赛，其中有75名男生两科竞赛都参加了，那么只参加数学竞赛而没有参加语文竞赛的女生有多少人?

    A．15

    B．25

    C．65

    D．75


    正确答案：A
    [答案] A。[解析]此题为比较复杂的容斥问题，有75名男生两科竞赛都参加了，因此至少参加了一项竞赛的男生有120+80-75=125人，那么至少参加一项竞赛的女生有260-125=135人，那么只参加数学竞赛没有参加语文竞赛的女生有135-120=15人。

  • 第14题：

    学生成绩表包括：学号、姓名、数学、语文、计算机、总成绩6个字段，其中数学、语文、计算机和总成绩字段均为N型。要将每个学生的数学、语文、计算机3科成绩汇总后存入“总成绩”字段中，应该使用的命令是______。

    A．REPLACE总成绩WITH数学+语文+计算机

    B．SUM数学+语文+计算机TO总成绩

    C．TOTALON总成绩FIELDS数学，语文，计算机

    D．REPLACEALL总成绩WITH数学+语文+计算机


    正确答案：D

  • 第15题：

    李木在某次考试中，课程甲和课程乙得178分，课程丙和课程丁得171分，课程乙和科程丙得174分，课程丁比课程甲高1分。问李木四门科程中哪门课程得分最高？

    A. 课程甲
    B. 课程乙
    C. 课程丙
    D. 课程丁

    答案：B
    解析：
    由题意可得： ，由①-③可知，甲丙；③-②可知，乙丁；④可知丁甲，故乙最大。

  • 第16题：

    小李在期末考试中，政治、语文、数学、英语、生物五科的平均分是88分，政治、数学两科的 平均分是90. 5分,语文、英语两科的平均分是83分，政治、英语两科的平均分是85分，而 且英语比语文多10分。问小李这次考试的数学成绩应是多少分？（ ）



    A. 96
    B. 97
    C. 98
    D. 99

    答案：D
    解析：
    注意到语文和英语给了两个条件，可以从这个条件入手求出成绩。英语 比语文多10分，因此英语应该比英语、语文的平均分多5分，即83 + 5 = 88(分）。因此，可求 得政治的得分为85X2 —88 = 82(分），再求得数学得分为90. 5X 2 — 82 = 99(分）。

  • 第17题：

    已知：（1）若甲和乙都参加自学考试，则丙不参加自学考试。（2）只有乙参加自学考试，丁才会参加自学考试。（3）甲和丙都参加了自学考试。问：乙和丁是否参加了自学考试？请写出推导过程。


    正确答案: 根据已知条件（1）和（3），运用充分条件假言推理的否定后件式，可作如下推论：若甲和乙都参加自学考试，则丙不参加自学考试；丙参加了自学考试；所以，或者甲不参加，或者乙不参加自学考试。根据“甲不参加，或者乙不参加自学考试”和已知条件（3）中的“甲参加了自学考试”，运用选言推理的否定肯定式，可以推出：乙不参加自学考试。
    根据已知条件（2）“只有乙参加自学考试，丁才参加自学考试”和以上推出的“乙不参加自学考试”，运用必要条件假言推理的否定前件式，可以推出：丁不参加自学考试。由上述推论可知：乙不参加自学考试。由上述推论可知：乙不参加自学考试，丁不参加自学考试。

  • 第18题：

    “甲：你上学期语文、数学考试成绩怎么样？乙：我语文考得不错，得了80多分呢？” 上面乙的回答违反了合作原则的（）。

    • A、数量准则
    • B、关联准则
    • C、质量准则
    • D、方式准则

    正确答案:A

  • 第19题：

    单选题
    甲、乙、丙三人要装订语文和数学课本。装订语文课本的工作量比装订数学课本的工作量多1/4，甲、乙、丙三人单独完成数学课本的装订各需20天、24天和30天。为了共同完成这两项任务，先安排甲装订数学课本，乙、丙一起装订语文课本；经过几天后，又调丙去帮甲装订数学课本。最后两种课本的装订任务同时完成，那么乙、丙二人合作了（　　）天。
    A

    12

    B

    15

    C

    17

    D

    18


    正确答案： D
    解析：
    取20，24，30的最小公倍数120。设装订数学课本的工作量为120，那么装订语文课本的工作量为（1＋1/4）×120＝150，则甲、乙、丙每天完成的工作量分别是6，5，4。三人装订完两种课本共需要（120＋150）÷（6＋5＋4）＝18天。乙在18天中，一直在装订语文课本，完成了18×5＝90，剩下的装订语文课本的任务都由丙完成，需要（150－90）÷4＝15天。即乙和丙共合作了15天。

  • 第20题：

    问答题
    已知：（1）若甲和乙都参加自学考试，则丙不参加自学考试。（2）只有乙参加自学考试，丁才会参加自学考试。（3）甲和丙都参加了自学考试。问：乙和丁是否参加了自学考试？请写出推导过程。

    正确答案： 根据已知条件（1）和（3），运用充分条件假言推理的否定后件式，可作如下推论：若甲和乙都参加自学考试，则丙不参加自学考试；丙参加了自学考试；所以，或者甲不参加，或者乙不参加自学考试。根据“甲不参加，或者乙不参加自学考试”和已知条件（3）中的“甲参加了自学考试”，运用选言推理的否定肯定式，可以推出：乙不参加自学考试。
    根据已知条件（2）“只有乙参加自学考试，丁才参加自学考试”和以上推出的“乙不参加自学考试”，运用必要条件假言推理的否定前件式，可以推出：丁不参加自学考试。由上述推论可知：乙不参加自学考试。由上述推论可知：乙不参加自学考试，丁不参加自学考试。
    解析： 暂无解析

相关内容