人教版数学八年级上册第十一十二章测试题(含答案)

若正方形ABCD的边长为4，E为BC边上一点，BE＝3，M为线段AE上一点，射线BM交正方形的一边于点F，且BF＝AE，则BM的长为______________ ．


正确答案：

如图所示，点P为正方形ABCD内一点，且PA=1，PB=2,PC=3试求∠ABP的度数？

请教:2012年初中数学《函数及其图象》测验卷第2大题第1小题如何解答?

【题目描述】

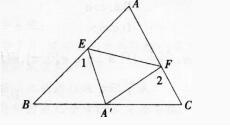
如果点P（－1,b）在直线y=2x+3上，那么点P到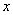轴的距离为__________.

 


【参考答案分析】：

1

如图．已知圆⊙O是△ABC的外接圆，AD是圆⊙0的直径，且BD=BC，延长AD到E，且有∠EBD=∠CAB。

(1)求证：BE是⊙0的切线；
(2)若BC=√3，AC=5，求圆的直径AD及切线BE的长。


答案：
解析：
(1)连接OB，∵AD是圆⊙O的直径'∴∠OBD+∠EBD=90°， ∵BD=BC,∴其劣弧所对的圆周角相等，即∠CAB=∠BAD，
∵AO=BO,∴∠BAD=∠ABO，
又∠EBD=∠CAB,∴∠EBD=ABO,∴∠OBD+∠ABO=90°,∴∠OBE=90°，
∵B0是圆的半径，∴BE是⊙O的切线。
(2)设圆的半径为r，连接CD交OB于F，

设圆的半径为R，连接CD，.

(6分)如图，点P为矩形ABCD边BC上一点(不包括端点)，E为BC延长线上一点，CQ为∠DCE的角平分线，连接AP，PQ，使AP⊥PQ。求证：当AB=BC时，存在AP=PQ。


答案：
解析：

∴AP=PQ。

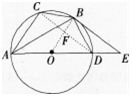
摘要:八年级数学第十一十二章解答题1、已知：如图，在直线MN上求作一点P，使点P到∠AOB两边的距离相等。(不写作法，保留作图痕迹）2、如图，在△ABC中，AD，AE分别是边BC上的中线和高，（1）若AE=3cm，S△ABC=12cm2.求DC的长.（2）若∠C-∠B=300，求∠DAE的大小.3、在△ABC中，AD是∠BAC的平分线，E、F分别为AB、AC上的点，且∠EDF+∠EAF=180°，求证DE=DF．4.如图所示，∠ACD是△ABC的外角，∠A=40°，BE平分∠ABC，CE平分∠ACD，且BE、CE交于点E．（1）求∠E的度数．（2）请猜想∠A与∠E之间的数量关系，请说明理由． 5.（1）已知，如图①，在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E，求证：DE=BD+CE．（2）如图②，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意钝角，请问结论DE=BD+CE是否成立？若成立，请你给出证明：若不成立，请说明理由．6．如图，已知△ABC中，AB=AC=6cm，∠B=∠C，BC=4cm，点D为AB的中点．（1）如果点P在线段BC上以1cm/s的速度由点B向点C运动，同时，点Q在线段CA上由点C向点A运动．①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？（2）若点Q以②中

如图，把△ABC沿折痕删折，顶点A恰好落在边BC上的点A'处，若∠A=70o，则∠1+∠2的度数是______ 。


答案：
解析：
140°。解析：根据三角形的性质，得∠1+∠B+∠2+∠C=EA'C+∠FA'B=180°+∠EA'F=180°+∠A， 所以∠1+∠2=180°+∠A-∠B-∠C=2∠A=140°。

如图：已知圆0，点P在圆外，D，E在圆上，PE交圆于C，PD与圆相切，G为CE上一点且满足PG=PD,连接DG并延长交圆于A，作弦AB⊥EP，垂足为F。

(1)求证：AB为圆的直径；
(2)若AC=BD，AB=5，求弦DE的长。


答案：
解析：
(1)证明：∵PG=PD,∴∠PGD=∠PDG，又∵∠AGF=∠PGD，∠PDG=∠ABD，∴∠AGF=∠ABD，∴∠ADB=∠AFP=90°，∴AB为圆的直径。

已知函数f(x)=㏑(x+2)-x2+bx+c，
(1)若点P(-1，0)在f(x)的图象上，过点P的切线与直线y=-x+2平行，求f(x)的解析式；
(2)若f(x)在区间[0，2]上单调递增，求b的取值范围。


答案：
解析：

如图所示，已知A，B为直线L：y=mx-m+2与抛物线y=x2的两个交点。
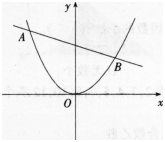
(1)直线ι经过一个定点C，试求出点C的坐标；(2分)
(2)若m=-1，已知在直线L下方的抛物线上存在一点P(点P与坐标原点0不重合)，且△ABP的面积为（3√13）/2，求点P的坐标。(6分)


答案：
解析：
(1)直线L：y=m(x-1)+2，当x=1时，y的取值与m无关，此时y=2，所以直线过定点(1，2)；

如图，在四边形ABCD中，∠ABC=90°，CD⊥AD，AD2+CD2=2AB2.

(1)求证：AB=BC；
(2)当BE⊥AD于E时，试证明：BE=AE+CD.


答案：
解析：



更多 “人教版数学八年级上册第十一十二章测试题(含答案)” 相关考题
考题 如图，在A、B两点，放置两个点电荷，它们的带电量分别为q---1,q---2，MN是过A、B的直线，P是直线上的一点，若P点的场强为0，则（　　）。 答案：B解析：电场强度是矢量，当空间的电场是由几个点电荷共同激发的时候，空间某点的电场强度等于每个点电荷单独存在时所激发的电场在该点的场强的矢量和。若两个点电荷电性相同，则P点的电场一定
查看答案
考题 如图，在直三棱柱ABC—A1B1C1中，E，F分别是A1B，A1C的中点，点D在B1C，上，A1D⊥B1C，求证：(8分) (1)EF∥平面ABC； (2)平面A1FD上平面BB1C1C． 答案：解析：证明：(1)由E，F分别是A1B1A1C的中点知，EF∥BC，
查看答案
考题 如图，在一张矩形纸片ABCD中，AB=4，BC=8。点E，F分别在AD，BC上，将纸片ABCD沿直线EF折叠，点C落在AD上的一点日处，点D落在G处，有以下四个结论：①四边形CFHE是菱形；②EC平分∠DCH；③线段BF的取值范围为3≤BF≤4；④当点H与点A重合时, 。以上结论中，你认为正确的有( )个。 A.1 B.2 C.3 D.4 答案：C解析：
查看答案
考题 如图在ΔABC中，DE∥BC，若AD：DB=1：3，DE=2，则BC等于( )。 A.8 B.6 C.4 D.2 答案：A解析：由于DE∥BC,所以DE：BC=AD：AB，又由AD:DB=1：3，所以AD：AB=1:4，由DE=2得BC=8。
查看答案
考题 如图，已知△ABC的两条角平分线AD和CE相交于H，∠B=60。，F在AC上，且AE=AF． (1)证明：B，D，H，E四点共圆； (2)证明：CE平分∠DEF． 答案：解析：证明：(1)在△ABC中，因为∠B=60°， 所以∠BAC+∠BCA=120°． 因为AD，CE是角平分线． 所以∠HAC+∠HCA=60°，故∠AHC=120°． 于是∠EHD=∠AHC=120°． 因为∠EBD+∠EHD=180°．所以B，D，H，E四点共圆． (2)连接BH，则BH为∠ABC的平分线，得∠HBD=30°， 由(1)知B，D，H，E四点共圆，所以∠CED=∠HBD=30°． 又∠AHE=∠EBD=60°，由已知AE=AF，AD平分∠EAF， 可得EF⊥AD，所以∠CEF=30°．所以CE平分∠DEF．
查看答案
考题 如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AB=4，BC=3，AD=5，∠DAB=∠ABC=90o，E是CD的中点。 (1)证明：CD⊥平面PAE； (2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等，求四棱锥P-ABCD的体积。 答案：解析：
查看答案
考题 如图，在Rt△ABC中，∠C=90o,AC=6，BC=8，动点P由起点A沿边AB向终点B运动，每秒2个单位，动点Q由起点B沿边BC向终点C运动，每秒1个单位，P、Q两点同时由起点开始运动，记运动时间为t秒。 (1)设△BPQ的面积为S，求S的最大值： (2)当△BPQ与△ABC相似时，求t的值。 答案：解析：
查看答案
考题 如图，Rt△ABC中，AB=6，BC=4，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为__________。 答案：解析：
查看答案
考题 若正方形ABCD的边长为4，E为BC边上一点，BE=3，M为线段AE上的一点，射线BM交正方形的一边于点F，且BF=AE，则BM的长为5/2或12/5。正确答案:错误
查看答案
考题 如图，四棱锥S-ABCD的底面是矩形，SA⊥底面ABCD，P是BC边的中点，AD=2，SA=AB=1。 (1)求证：PD⊥平面SAP； (2)求三棱锥S-APD的体积。 答案：解析：(1)证明：易知在△APD中，，AD=2，满足勾股定理，故PD⊥AP。SA⊥底面ABCD，则SA⊥PD。PD同时垂直于平面SAP内的两条相交直线，PD⊥平面SAP。 (2)
查看答案
相关内容
最新试卷
热门试卷