(10分)如图，几何体A1B1C1-ABC中，AB=AC，AB⊥AC，棱AA1，BB1，CC1都垂直于面ABC，BC=AA1=2BB1=2CC1=4，D为B1C1的中点，E为A1D的中点。 求证：(1)AE⊥BC；(3分) (2)求异面直线AE与DC所成角的余弦值。(7分)

题目
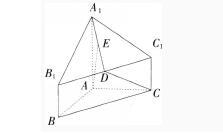
(10分)如图，几何体A1B1C1-ABC中，AB=AC，AB⊥AC，棱AA1，BB1，CC1都垂直于面ABC，BC=AA1=2BB1=2CC1=4，D为B1C1的中点，E为A1D的中点。
求证：(1)AE⊥BC；(3分)
(2)求异面直线AE与DC所成角的余弦值。(7分)

相似考题

1.△ABC中，AB=3，BC=4，则AC边的长满足（ ）。A．AC=5B．AC>1C．AC<7D．1<AC<7

2.在 △ABC中，∠C=90°，AB=10。（1）∠A=30°，求BC，AC（精确到0.01）；（2）∠A=45°，求BC，AC（精确到0.01）。

3.△ABC中，AB=13cm，BC=10cm，BC边上的中线AD=12cm.求AC

4.有如下嵌套的if语句： if(a<b) if(a<c)k=a； else k=C： else if(b<c)k=b； else k=C； 以下选项中与上述if语句等价的语句是（ ）。A.k=(a<b)?a：b；k=(b<c)?b：C；B.k=(a<b)?((b<c)?a：b)：((b>c)?b：c)；C.k=(a<b)?((a<c)?a：c)：((b<c)?b：c)；D.k=(a<b)?a：b；k=(a<c)?a：c；

参考答案和解析
答案：
解析：

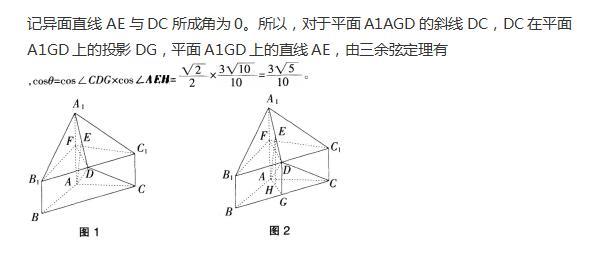
更多“(10分)如图，几何体A1B1C1-ABC中，AB=AC，AB⊥AC，棱AA1，BB1，CC1都垂直于面ABC，BC=AA1=2BB1=2CC1=4，D为B1C1的中点，E为A1D的中点。 ”相关问题

  • 第1题：

    在△ABC中，D、E分别是边AB、AC的中点，若BC＝5，则DE的长是（ ）。

    A．2.5

    B．5

    C．10

    D．15


    正确答案：A
    分析：由D、E分别是边AB、AC的中点可知，DE是ABC的中位线，根据中位线定理可知，DE＝BC＝2.5。
    涉及知识点：中位线
    点评：本题考查了中位线的性质，三角形的中位线是指连接三角形两边中点的线段，中位线的特征是平行于第三边且等于第三边的一半。
    推荐指数：★★

  • 第2题：

    试用卡诺图化简如下逻辑函数式。(1) Y1=ABC＋ABC－＋B－(2) Y2=A＋AB－C＋AB(3) Y3=AC－＋AB－＋AB(4) Y4=AB－C－＋AC－＋C


    答案：(1) Y1=ABC+ABC-+B-(2) Y2=A+AB-C+AB(3) Y3=AC-+AB-+AB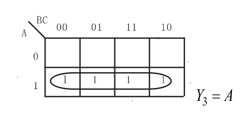(4) Y4=AB-C-+AC-+C

  • 第3题：

    如图2-7所示，三棱镜ABC，∠A=30°.光线垂直AB面射入棱镜，由AC面射出.已知出射光与入射光的夹角为30°.在Ac面上光线的入射角是（），棱镜的折射率是（）.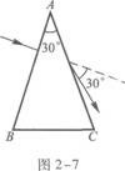


    答案：
    解析：
    30°1．73 【解题指要】本题的考点是光的反射定律和折射定律．
    光线经过两次折射，第一次在AB面上，第二次在AC面上，在AB面上垂直入射，入射角为
    零，折射角也为零．此折射光线是AC面上的入射光．它与AC面的夹角为
    90°－∠A=90°－30°=60°
    因此，AC面上光线的入射角是
    θi=90°－60°=30°
    由图2-15知，光线在AC面上折射后的折射光（即出射光）与AC面法线的夹角（即折射角）为
    θr=30°+30°=60°
    再根据折射定律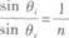

    知棱镜的折射率为

    注意，考生在解题时应在图2-7中把AC面上通过入射点的AC的垂线，即AC面的法线画出，这样根据几何关系可以明确求出折射角θr(见图2-15)．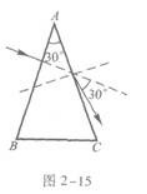

  • 第4题：

    如图，Rt△ABC中，∠ABC=90o,AB=28 cm，以AB为直径的半圆与AC相交，图中的阴影部分①的面积比⑦的面积少28.28 cm2，求BC的长(π取3．14)。


    答案：
    解析：

  • 第5题：

    在△ABC中，已知AB＝5，AC＝3，∠A＝120°，则BC长为



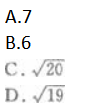    答案：A
    解析：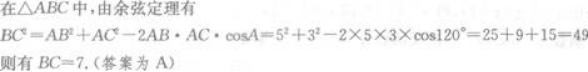

  • 第6题：

    在△ABC中，AB=2，BC=3，B=60°．求AC及△ABC的面积．


    答案：
    解析：
    解：由余弦定理得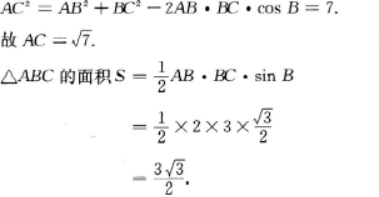

  • 第7题：

    在三角形ABC，AB=4，AC=6，BC=8，D为BC的中点，则AD=




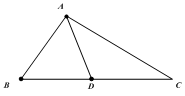
    答案：B
    解析：

  • 第8题：

    已知△ABC的三边长AC＝3，BC＝4，AB＝5，P为AB边上任意一点，则CP→ (BA→－BC→)的最大值为(　　)

    A、8
    B、9
    C、12
    D、15

    答案：B
    解析：

  • 第9题：

    如图，Rt△ABC中，AB=6，BC=4，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为__________。



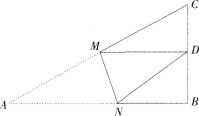    答案：
    解析：

  • 第10题：

    如图，正方体ABCD-A1B1C1D1中，E，F，G分别为AA1，A1D1，BC的中点，则异面直线EF与D1G所成角的大小为__________。



    答案：
    解析：
    连接AD1，AG，由于EF平行于AD1，则异面直线EF与D1G所成角等于AD1与D1G所成角。设正方体棱长为2，在△AD1G中，D1G=3，根据余弦定理，cos∠AD1G=

  • 第11题：

    有一镗削工件，三孔ABC的坐标尺寸如图，为检验上的需要，计算三孔ABC的中心距尺寸，正确的是（）。

    • A、AB=26.93，BC=23.35，AC=27.2
    • B、AB=26.93，BC=20.23，AC=26.5
    • C、AB=25.03，BC=23.35，AC=27.2
    • D、AB=25.03，BC=20.23，AC=27.2

    正确答案:A

  • 第12题：

    单选题
    如图所示，力P作用在BC杆的中点，且垂直于BC杆，若P=kN，杆重不计。则杆AB的内力大小S为（　）
    A

    1kN

    B

    0．5kN

    C

    1．41kN

    D

    2kN


    正确答案： D
    解析： 暂无解析

  • 第13题：

    试证明如下逻辑函数等式。(1) AB－＋AB－C=AB－;(2) AB(C＋C－)＋AC=AB＋AC;(3) A(BC＋BC)＋AC=A(BC)＋AC


    答案：(1)左边=AB-+AB-C=AB-(1+C)=AB-=右边(2)左边=AB(C+C-)+AC=AB+AC=右边(3)左边=A(BC+BC)+AC=A(BC)+AC=右边

  • 第14题：

    设A、B、C为随机事件，则( )。

    A.P(A-B-C)=P(A)-P(AB)-P(AC)-P(BC)+P(ABC)
    B.P(A-B-C)=P(A)-P(AB)-P(AC)+P(ABC)
    C.P(A-B-C)=P(A)-P(AB)-P(BC)+P(ABC)
    D.P(A-B-C)=P(A)-P(AC)-P(BC)+P(ABC)

    答案：B
    解析：

  • 第15题：

    如图,D是△ABC内的一点，BD⊥CD，AD=6，BD=8，CD=6，E，F，G，H分别是AB，AC，CD， BD的中点．则四边形EFGH的周长是()。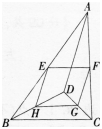

    A.12
    B.14
    C.15
    D.16

    答案：D
    解析：
    因为BD⊥CD，BD=8，CD=6，由勾股定理可知BC=10。由三角形中位线定理可知EH=FG=

  • 第16题：

    如图，三棱柱ABC-A1B1C1，M，N分别为AB，B1C1的中点，
    (1)求证MN∥平面AA1C1C；
    (2)若C1C=CB1，CA=CB，平面CC1B1B⊥平面ABC，求证：AB⊥平面CMN。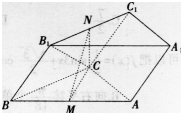


    答案：
    解析：

  • 第17题：

    在△ABC中，AB=2，BC=3，B=60°，BD为AC边上的高．求AC，BD．


    答案：
    解析：

  • 第18题：

    在 ABC中，∠ABC=600，AB=4，BC=6，则AC=（）


    答案：C
    解析：

  • 第19题：

    如图所示，有一束平行于等边三棱镜截面ABC的单色光从空气射向E点，并偏折到F点。已知入射方向与边AB的夹角为θ=30。，E、F分别为边AB、BC的中点，则（　　）。




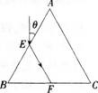    答案：C
    解析：


    不变，光速变小，波长变小，故选C。

  • 第20题：

    如图1，在△ABC中，BC = 8 cm，AB的垂直平分线交AB于点Ｄ， 交边AC于点E，△BCE的周长等于18 cm，则AC的长等于（ ）

    A、6cm　
    B、8cm
    C、10cm　　
    D、12cm

    答案：C
    解析：

  • 第21题：

    如图，已知四棱锥P-ABCD底面ABCD为矩形，侧棱PA⊥ABCD，AB=AP=21/2AD=2，E，F分别为PC，AB的中点。
    (I)证明：EF∥面PAD。
    (II)求三棱锥B-PFC的体积。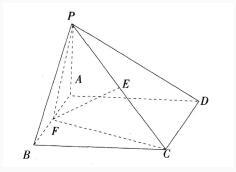


    答案：
    解析：

  • 第22题：

    逻辑函数Y=ABC+AC+BC的最简式为（）

    • A、Y=C
    • B、Y=BC+AB+BC
    • C、Y=ABC+AC+BC
    • D、Y=1

    正确答案:A

  • 第23题：

    Y=AB+BC+A=（）。

    • A、A+BC
    • B、A
    • C、BC
    • D、ABC

    正确答案:A

相关内容