华南理工线代精选试题
A.实对称阵
B.有n个相异特征值的n阶阵
C.有n个线性无关的特征向量的n阶方阵
A.对称矩阵
B.可逆矩阵
C.n阶矩阵的转置矩阵
D.线性方程组的系数矩阵
A、转置运算不改变方阵A的行列式值和秩
B、若m C、已知同阶方阵A,B和C满足AB=AC,若A是非奇异阵,则B=C D、若矩阵A的列向量线性相关,则A的行向量也线性相关
此题为判断题(对,错)。
A、A=0
B、A=E
C、r(A)=n
D、0r(A)(n)
若是6阶方阵A的伴随矩阵,且rank(A)=4, 则rank()=( ).2.设,则( )。3设是的子空间,则空间的维数是( )。4对称矩阵A的全部特征根是4,-5,3,2,若已知矩阵为正定矩阵,则常数必须大于数值( )。5已知n阶矩阵,则矩阵A的逆是二选择题(15分)若A,B是n阶方阵,下列等式中恒等的表达式是( )A., B. , C. | A+B|=|A|+|B|, D.
若A是n阶方阵,则为正交矩阵的充要条件不是().的列向量构成的单位正交基,的行向量构成的单位正交基,
若是空间的一个k维子空间,是的一组基;是空间的一个k维子空间, 是的一组基.且,则( )A.向量组可以由向量组线性表示,B. 向量组可以由向量组线性表示,C. 向量组与向量组可以相互线性表示,D. 向量组与向量组不能相互线性表示.
若是实对称阵A的两个不同特征根,是对应的特征向量,则下列命题哪一个不成立( )A. 都是实数, B. 一定正交,C. 有可能是A的特征向量。 D. 有可能是A的特征根.
已知A为n+1阶方阵,且rank(A)=k, 非齐次线性方程组Ax=B的(n-k+1)个线性无关解为, 则Ax=B的通解为( D )A. , B. ,C. ,D.
1.若A为3阶方阵,且|A|=1/2,求
设, 求矩阵.
计算向量在基下的坐标.
设向量组求向量组的一个最大无关组.5.利用分块矩阵方法,计算的逆矩阵.
设n维量组和向量组有关系, 问n维向量组与是否同秩?证明你的结论.
二次型, 通过正交变换可将此二次型化为标准型,求参数及所用的正交变换.
求线性方程组的通解.
解矩阵方程,并写出解方程时初等矩阵的变换过程:.
设A为4阶方阵,且A的特征根互不相同, 证明:(1)方阵A有4个线性无关的特征向量.(2) 方阵A可以对角化.
A.A的n个特征向量两两正交
B.A的n个特征向量组成单位正交向量组
C.A的k重特征值λ0,有r(λ0E-A)=n-k
D.A的k重特征值λ。,有r(λ0E-A)=k

设A是欧氏空间V关于基a₁,a₂...an的度量矩阵,a₁,a₂...an是标准正交基的充分必要条件是()。
A. A是正交矩阵
B. A是单位矩阵
C. A是对称阵
D. A是矩阵
A、单位
B、对称
C、实
D、正交
设A为m×n阶矩阵,则齐次线性方程组AX=0只有零解的充分必要条件是(64)。
A.A的列向量组线性无关
B.A的列向量组线性相关
C.A的行向量组线性无关
D.A的行向量组线性相关
A.A的列向量组线性无关
B.A的列向量组线性相关
C.A的行向量组线性无关
D.A的行向量组线性相关
解析:齐次线性方程组AX=0只有零解的充分必要条件是A的列向量组线性无关
B.矩阵C的列向量组与矩阵A的列向量组等价
C.矩阵C的行向量组与矩阵B的行向量组等价
D.矩阵C的列向量组与矩阵B的列向量组等价
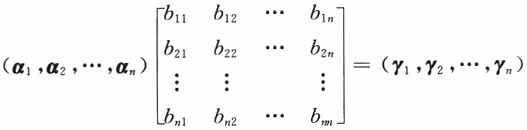
可见
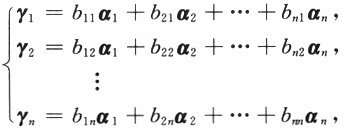
即C的列向量组可以由A的列向量组线性表出.
因为B可逆,有CB^-1=A.类似地,A的列向量组也可由C的列向量组线性表出,因此选(B).
