设A是m×n非零矩阵,B是n×l非零矩阵,满足AB=0,以下选项中不一定成立的是: A. A的行向量组线性相关 B. A的列向量组线性相关 C. B的行向量组线性相关 D. r(A)+r(B)≤n
题目
设A是m×n非零矩阵,B是n×l非零矩阵,满足AB=0,以下选项中不一定成立的是:
A. A的行向量组线性相关
B. A的列向量组线性相关
C. B的行向量组线性相关
D. r(A)+r(B)≤n
B. A的列向量组线性相关
C. B的行向量组线性相关
D. r(A)+r(B)≤n
相似考题
参考答案和解析
答案:A
解析:
A、B为非零矩阵且AB=0,由矩阵秩的性质可知r(A)+r(B)≤n,而A、B为非零矩阵,则r(A)≥1,r(B)≥1,又因r(A)m×n的列向量相关×,1≤r(B)<n,Bn×l的行向量相关,从而选项B、C、D均成立。
更多“设A是m×n非零矩阵,B是n×l非零矩阵,满足AB=0,以下选项中不一定成立的是: ”相关问题
-
第1题:
设A是m×n非零矩阵,B是n×l非零矩阵,满足AB=0,以下选项中不一定成立的是:A. A的行向量组线性相关
B. A的列向量组线性相关
C. B的行向量组线性相关
D. r(A)+r(B)≤n答案:A解析:A、B为非零矩阵且AB=0,由矩阵秩的性质可知r(A)+r(B)≤n,而A、B为非零矩阵,则r(A)≥1,r(B)≥1,又因r(A)m×n的列向量相关×,1≤r(B)<n,Bn×l的行向量相关,从而选项B、C、D均成立。 -
第2题:
设A,B是n阶矩阵,且B≠0,满足AB=0,则以下选项中错误的是: 答案:D解析:解根据矩阵乘积秩的性质,AB=0,有r(A)+r(B)≤n成立,选项A正确。AB =0,
答案:D解析:解根据矩阵乘积秩的性质,AB=0,有r(A)+r(B)≤n成立,选项A正确。AB =0,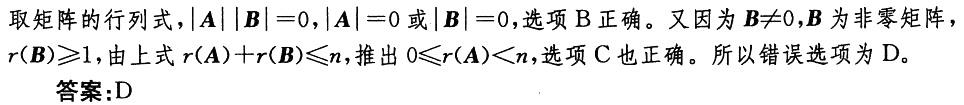
-
第3题:
设A,B是n阶矩阵,且B≠0,满足AB=0,则以下选项中错误的是:
A.r(A)+r(B)≤n B. A =0 或 B =0 C. 0≤r(A)答案:D解析:提示:根据矩阵乘积秩的性质,AB=0,有r(A)+r(B)≤n成立,选项A正确。AB=0,取矩阵的行列式, A B =0, A =0或 B =0,选项B正确。又因为B≠0,B为非零矩阵, r(B)≥1,由上式r(A) + r(B)≤n,推出0≤r(A) -
第4题:
设A为n阶矩阵,证明:r(A)=1的充分必要条件是存在n维非零列向量α,β使得A=αβT.答案:解析:
-
第5题:
若矩阵A= ,B是三阶非零矩阵,满足AB=O,则t=_______.答案:1、1解析:由AB=0得r(A)+r(B)≤3,因为r(B)≥1,所以r(A)≤2,又因为矩阵A有两行不成比例,所以r(A)≥2,于是r(A)=2.
,B是三阶非零矩阵,满足AB=O,则t=_______.答案:1、1解析:由AB=0得r(A)+r(B)≤3,因为r(B)≥1,所以r(A)≤2,又因为矩阵A有两行不成比例,所以r(A)≥2,于是r(A)=2.
由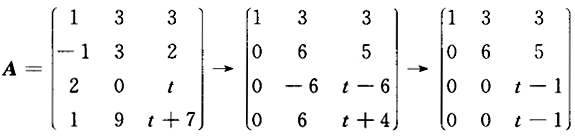 得t=1.
得t=1. -
第6题:
设 都是n(n≥3)阶非零矩阵,且AB=O,则r(B)=( )A. 0
都是n(n≥3)阶非零矩阵,且AB=O,则r(B)=( )A. 0
B.1
C. 2
D. 3答案:B解析:
-
第7题:
设A是m×n矩阵,如果mA.Ax=b必有无穷多解
B.Ax=b必有唯一解
C.Ax=0必有非零解
D.Ax=0必有唯一解答案:C解析:根据条件可知,方程组中方程的个数一定小于未知数的个数,所以Ax=0必有非零解。由
-
第8题:
设A,B均为n阶非零矩阵,且AB=0,则RA,RB满足()。
- A、必有一个等于0
- B、都小于n
- C、一个小于n,一个等于n
- D、都等于n
正确答案:B -
第9题:
单选题设A是m×n矩阵,则m<n是齐次线性方程组ATAX(→)=0(→)有非零解的( )。A必要条件
B充分条件
C充要条件
D以上都不对
正确答案: D解析:
充分性:因r(ATA)≤r(A)≤m<n,其中n是ATA的阶数,即方程组ATAX=0的未知数的个数,故方程组ATAX=0有非零解;但不必要,因为当m≥n时,r(ATA)≤n≤m,此时方程组可能只有零解,也可能有非零解。 -
第10题:
填空题设,B为三阶非零矩阵,且AB=0,则t=____。正确答案: -3解析:
由B是三阶非零矩阵,且AB=0,知B的列向量是方程组AB=0的解且为非零解,故|A|=0,解得t=-3。 -
第11题:
单选题设A,B均为n阶非零矩阵,且AB=0,则RA,RB满足()。A必有一个等于0
B都小于n
C一个小于n,一个等于n
D都等于n
正确答案: C解析: 暂无解析 -
第12题:
单选题若A为m×n矩阵,B为n×m矩阵,则( ).A当m>n时ABX=0必有非零解
B当m>n时AB必可逆
C当n>m时ABX=0只有零解
D当n>m时必有r(AB)<m
正确答案: C解析:
r(AB)≤r(A)≤n<m,AB是m阶方阵,由于系数矩阵的秩小于未知数的个数,故ABX=0有非零解. -
第13题:
设A、B均为n阶非零矩阵,且AB=0,则R(A),R(B)满足:A.必有一个等于0
B.都小于n
C. 一个小于n,一个等于n
D.都等于n答案:B解析:提示:利用矩阵的秩的相关知识,可知A、B均为n阶非零矩阵,且AB=0,则有 R(A)+R(B)≤n,而 A、B 已知为 n 阶非零矩阵,1≤R(A)≤n,1≤R(B)≤n,所以 R(A)、 R(B) 都小于n。 -
第14题:
设A是mxn的非零矩阵,B是nxl非零矩阵,满足AB=0,以下选项中不一定成立的是:
A. A的行向量组线性相关 B. A的列向量组线性相关
C.B的行向量组线性相关 D.r(A)+r(B)≤n答案:A解析:提示:A、B为非零矩阵且AB = 0,由矩阵秩的性质可知r(A)+r(B)≤n,而A、B为非零矩阵,则r(A)≥1,r(B)≥1,又因r(A)mxn的列向量相关,1≤r(B)nxl的行向量相关,从而选项B、C、D均成立。 -
第15题:
设A、B均为n阶非零矩阵,且AB=0,则R(A),R(B)满足:
A.必有一个等于0 B.都小于n
C. 一个小于n,一个等于n D.都等于n答案:B解析:提示:利用矩阵的秩的相关知识,可知A、B均为n阶非零矩阵,且AB = 0,则有R(A)+ R(B)≤n,而已知为n阶非零矩阵,1≤R(A)≤n,1≤R(B)≤n,所以R(A)、R(B)都小于n。 -
第16题:
设矩阵 是4阶非零矩阵, 且满足
是4阶非零矩阵, 且满足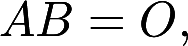 证明矩阵B的秩答案:解析:
证明矩阵B的秩答案:解析:
-
第17题:
设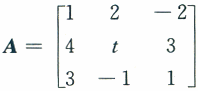 ,B为三阶非零矩阵,且AB=0,则t=________.答案:1、-3.解析:由AB=0,对B按列分块有AB=A(β1,β2,β3)=(Aβ1,Aβ2,Aβ3)=(0,0,0),即β1,β2,β3是齐次方程组Ax=0的解,又因B≠0,故Ax=0有非零解,那么
,B为三阶非零矩阵,且AB=0,则t=________.答案:1、-3.解析:由AB=0,对B按列分块有AB=A(β1,β2,β3)=(Aβ1,Aβ2,Aβ3)=(0,0,0),即β1,β2,β3是齐次方程组Ax=0的解,又因B≠0,故Ax=0有非零解,那么 若熟悉公式:AB=0,则r(A)+r(B)≤n.可知r(A)<3.亦可求出t=-3.
若熟悉公式:AB=0,则r(A)+r(B)≤n.可知r(A)<3.亦可求出t=-3.
【评注】对于AB=O要有B的每个列向量都是齐次方程组Ax=0的构思,还要有秩r(A)+r(B)≤n的知识. -
第18题:
设A,B是n阶矩阵,且B≠0,满足AB=0,则以下选项中错误的是:
A.r(A)+r(B)≤n B.A =0 或
B =0
C. 0≤r(
D)答案:D解析:提示 根据矩阵乘积秩的性质,AB=0,有r(A)+r(B)≤n成立,选项A正确。AB=0,取矩阵的行列式, A B =0, A =0或 B =0,选项B正确。又因为B≠0,B为非零矩阵, r(B)≥1,由上式r(A) + r(B)≤n,推出0≤r(A) -
第19题:
若A为m×n矩阵,B为n×m矩阵,则( ).A.当m>n时ABX=0必有非零解
B.当m>n时AB必可逆
C.当n>m时ABX=0只有零解
D.当n>m时必有r(AB)<m答案:A解析:r(AB)≤r(A)≤n<m,AB是m阶方阵,由于系数矩阵的秩小于未知数的个数,故ABX=0有非零解. -
第20题:
单选题设A是m×n的非零矩阵,B是m×1非零矩阵,满足AB=0,以下选项中不一定成立的是:()AA的行向量组线性相关
BA的列向量组线性相关
CB的行向量组线性相关
Dr(A)+r(B)≤n
正确答案: C解析: 由于AB=0,得到r(A)+r(B)≤n,又由于A,B都是非零矩阵,则r(A)>0,r(B)>0,得r(A)<nr(B)<n。因此A的列向量组线性相关,B的行向量组线性相关。 -
第21题:
单选题设A,B是n阶矩阵,且B≠0,满足AB=0,则以下选项中错误的是:()ArA.+rB.≤n
B︱A︱=0或︱B︱=0
CC.0≤r
DA=0
正确答案: C解析: 暂无解析 -
第22题:
单选题设A是m×n矩阵,B是n×m矩阵,则( )。A当m>n时,必有|AB|≠0
B当m>n时,必有|AB|=0
C当n>m时,必有|AB|≠0
D当n>m时,必有|AB|=0
正确答案: C解析:
因r(AB)≤min[r(A),r(B)]≤min(m,n),且AB为m×m矩阵,则当m>n时,由r(AB)≤n,知AB为不可逆矩阵,故必有|AB|=0。 -
第23题:
单选题若A为m×n矩阵,B为n×m矩阵,则( )。A当m>n时,ABX=0必有非零解
B当m>n时,AB必可逆
C当n>m时,ABX=0只有零解
D当n>m时,必有r(AB)<m
正确答案: A解析:
r(AB)≤r(A)≤n<m,AB是m阶方阵,由于系数矩阵的秩小于未知数的个数,故ABX=0有非零解。 -
第24题:
单选题设A,B都是n阶非零矩阵,且AB=0,则A和B的秩( )。A必有一个等于零
B都等于n
C一个小于n,一个等于n
D都小于n
正确答案: B解析:
因为A,B都是n阶非零矩阵,所以A、B的秩≤n。若A的秩=n,则A可逆。由AB=0可知B=0,与已知B是n阶非零矩阵矛盾,所以A的秩<n。同理可推出B的秩<n,故选D项。
