已知函数由方程确定求的极值
题目
已知函数 由方程
由方程 确定求
确定求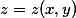 的极值
的极值
 由方程
由方程 确定求
确定求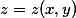 的极值
的极值相似考题
参考答案和解析
答案:
解析:
由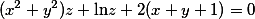 ,两边分别同时对x,y求偏导数得:
,两边分别同时对x,y求偏导数得: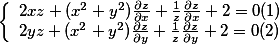 令(3)
令(3) 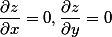 得:(4)
得:(4)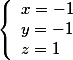
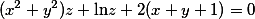 ,两边分别同时对x,y求偏导数得:
,两边分别同时对x,y求偏导数得: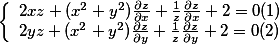 令(3)
令(3) 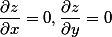 得:(4)
得:(4)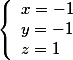
更多“已知函数由方程确定求的极值”相关问题
-
第1题:
(本题满分8分) 设函数z=z(x,y)是由方程x+y3+z+e2x=1所确定的隐函数,求dz.
正确答案:
-
第2题:
求函数
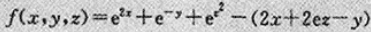 的极值。参考答案:
的极值。参考答案:
-
第3题:
求由方程2x2+y2+z2+2xy-2x-2y-4z+4=0确定的隐函数的全微分.答案:解析:
-
第4题:
求函数z=x2+y2+2y的极值.答案:解析:

-
第5题:
已知函数(x)=x4-4x+1.
(1)求(x)的单调区间和极值;
(2)求曲线y=(x)的凹凸区间.答案:解析: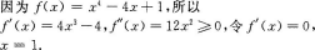
列表如下,

由表可知曲线(x)的单调递减区间为(-∞,1),单调递增区间为(1,+∞).由于"(x)=12x2≥0,所以为凹曲线,凹区间为(-∞,+∞),极小值为(1)=1-4+1=-2. -
第6题:
求方程 所确定的隐函数的导数
所确定的隐函数的导数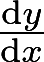 答案:解析:
答案:解析:
-
第7题:
由方程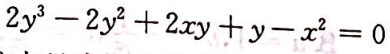 确定的函数y=y(x)A. 有驻点且为极小值点
确定的函数y=y(x)A. 有驻点且为极小值点
B. 有驻点且为极大值点
C. 有驻点但不是极值点
D. 没有驻点答案:A解析:
-
第8题:
已知函数y(x)由方程x^3+y^3-3x+3y-2=0确定,求y(x)的极值.答案:解析: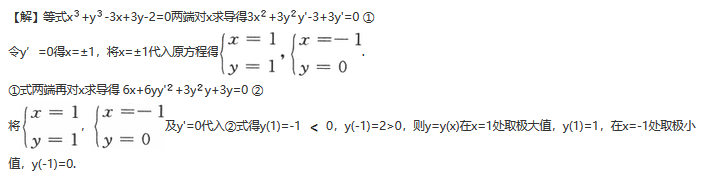
-
第9题:
已知微分方程y’+y=f(x),其中f(x)是R上的连续函数.
(Ⅰ)若f(x)=x,求方程的通解.
(Ⅱ)若f(x)是周期为T的函数,证明:方程存在唯一的以T为周期的解.答案:解析:【解】(Ⅰ)若f(x)=x,则方程为y'+y=x通解为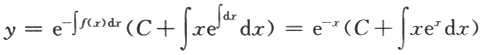
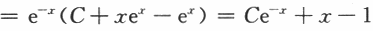
(Ⅱ)设y(x)为方程的任意解,则y'(x+T)+y(x+T)=f(x+T).
而f(x)周期为T,有f(x+T)=f(x).又y'(x)+y(x)=f(x).
因此y'(x+T)+y(x+T)-y'(x)-y(x)=0,有(e^x[y(x+T)-y(x)])'=0,
即e^x[y(x+T)=y(x)]=C.取C=0得y(x+T)-y(x)=0,
y(x)为唯一以T为周期的解. -
第10题:
已知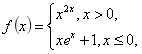 求
求 ,并求
,并求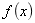 的极值。答案:解析:
的极值。答案:解析:
-
第11题:
求函数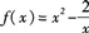 一的单调区间、极值及其曲线的凹凸区间和拐点.答案:解析:
一的单调区间、极值及其曲线的凹凸区间和拐点.答案:解析: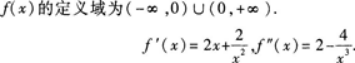
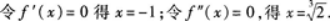
列表: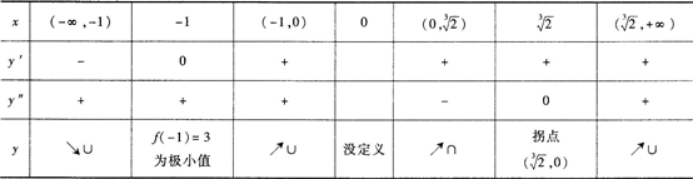
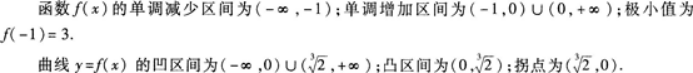
说明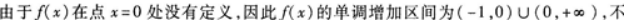

【评析】拐点(x0fx0))的坐标如果写成单一值x0或写为单一值fx0)都是错误的. -
第12题:
填空题已知函数y=y(x)由方程ey+6xy+x2-1=0所确定,则y″(0)=____。正确答案: -2解析:
ey+6xy+x2-1=0两边对x求导,得ey·y′+6xy′+6y+2x=0①。两边再对x求导,得ey·y″+ey(y′)2+6xy″+12y′+2=0②。当x=0时,y=0,将x=0,y=0代入①得y′(0)=0,再将x=y=y′(0)=0代入②得y″(0)=-2。 -
第13题:
已知消费函数C=30+0.8Y, 投资函数I=60-10r,求IS曲线方程.
参考答案:产品市场均衡条件为:I=S S=Y-C=0.2Y-30, I=60-10r
-
第14题:
已知由方程siny+xey,确定y是x的函数,则dy/dx的值是:
 答案:C解析:提示:式子两边对x求导,把式子中y看作是x的函数,计算如下:
答案:C解析:提示:式子两边对x求导,把式子中y看作是x的函数,计算如下:

@## -
第15题:
设函数f(x,y)=X2+Y2+xy+3,求f(x,y)的极值点与极值.答案:解析:
-
第16题:
设z=z(x,y)是由方程x2+y2+z2=ez所确定的隐函数,求dz.答案:解析:
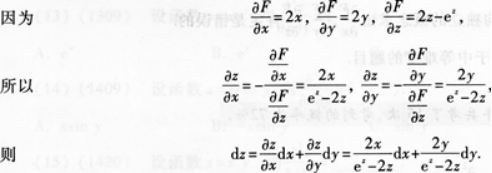
-
第17题:
求函数(x,y)=4(x-y)-x2-y2的极值.答案:解析:
所以(2,-2)=8为极大值. -
第18题:
设z=z(x,y)是由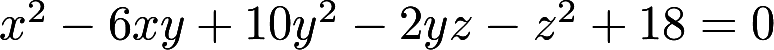 确定的函数,求
确定的函数,求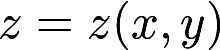 的极值点和极值答案:解析:
的极值点和极值答案:解析:
-
第19题:
求二元函数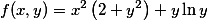 的极值。答案:解析:
的极值。答案:解析: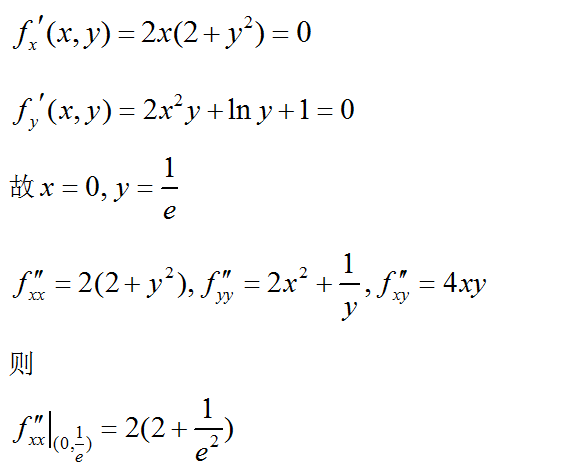
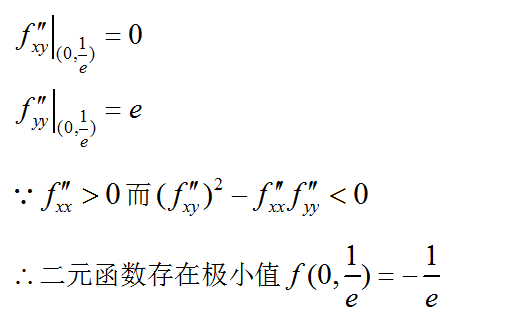
-
第20题:
设函数y=f(x)由方程y^3+xy^2+x^2y+6=0确定,求f(x)的极值.答案:解析:
-
第21题:
设函数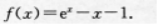
(I)求f(χ)的单调区间;
(Ⅱ)求f(χ)的极值.答案:解析:
-
第22题:
设Z=Z(x,Y)是由方程x+y3+z+e2=1确定的函数,求dz答案:解析:利用隐函数求偏导数公式,记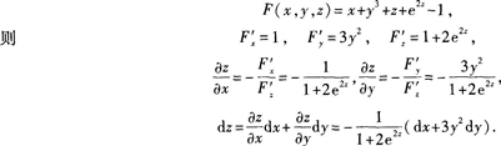
-
第23题:
问答题求由方程x2+y2+z2-xz-yz-2x-2y+2z-6=0确定的函数z=z(x,y)的极值。正确答案:
先求出函数z的各个偏导:
由原方程可得,原方程两边对x求导得
2x+2z·zx′-z-(x+y)zx′-2+2zx′=0①
原方程两边对y求导得
2y+2z·zy′-z-(x+y)zy′-2+2zy′=0②
①②中,令zx′=0,zy′=0,解得x=(z+2)/2,y=(z+2)/2,将其代入已知方程得Z=±4,故驻点为(3,3)和(-1,-1)。
①式两边对x,y分别求导得
2+2(zx′)2+2zzxx″-2zx′+(2-x-y)zxx″=0③
2zy′zx′+2zzxy″-zy′-zx′+(2-x-y)zxy″=0④
②式两边对y求导得
2+2(zy′)2+2zzyy″-2zy′+(2-x-y)zyy″=0⑤
当x=y=-1,z=-4时,zx′=zy′=0,将其代入③④⑤,得A=zxx″(-1,-1)=1/2,B=zxy″(-1,-1)=0,C=zyy″(-1,-1)=1/2,B2-AC=-1/4<0,A=1/2>0。
则函数z在(-1,-1)处取得极小值z=-4。
当x=y=3,z=4时,zx′=zy′=0,并将其代入③④⑤,得A=zxx″(3,3)=-1/2,B=zxy″(3,3)=0,C=zyy″(3,3)=-1/2,B2-AC=-1/4<0,A=-1/2<0。
故z在(3,3)点处取到极大值z=4。解析: 暂无解析
