一自动生产包装机包装食盐,每袋重量服从正态分布N（μ,σ^2）,任取9袋测得其平均重量为=99.078,样本方差为s^2=1.143^2,求μ的置信度为0.95的置信区间.

题目
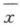一自动生产包装机包装食盐,每袋重量服从正态分布N（μ,σ^2）,任取9袋测得其平均重量为=99.078,样本方差为s^2=1.143^2,求μ的置信度为0.95的置信区间.

相似考题

1.采用包装机包装食盐,要求500g装一袋,已知标准差σ=3g,要使食盐每包平均质量的95%置信区间长度不超过4.2g,样本量n至少为________。A．4B．6C．8D．10

2.关于中心极限定理，下列说法正确的是( )。A．多个随机变量的平均值(仍然是一个随机变量)服从或近似服从正态分布B．几个相互独立同分布随机变量，其共同分布不为正态分布或未知，但其均值μ和方差σ2都存在，则在n相当大的情况下，样本均值X近似服从正态分布N(μ，σ2/n)C．无论什么分布(离散分布或连续分布，正态分布或非正态分布)，其样本均值X的分布总近似于正态分布D．设n个分布一样的随机变量，假如其共同分布为正态分布N(μ，σ2)，则样本均值X仍为正态分布，其均值不变仍为μ，方差为σ2/n

3.某企业生产的袋装食品采用自动打包机包装，每袋标准重量为100克。现从某天生产的一批产品中按重复抽样随机抽取50包进行检查，测得样本均值为：（1）确定该种食品平均重量95%的置信区间。（2）采用假设检验方法检验该批食品的重量是否符合标准要求？（写出检验的具体步骤）。

4.某糖厂生产袋糖，已知袋糖重量服从正态分布，规定平均重量不低于500g，今从一批袋糖中随机抽取12袋，测得＝510g，s=18g。检验袋糖平均重量是否符合规定的原假设H0为( )。A．μ=500B．μ≥500C．μ≤500D．μ≠500

参考答案和解析
答案：
解析：
更多“一自动生产包装机包装食盐,每袋重量服从正态分布N（μ,σ^2）,任取9袋测得其平均重量为=99.078,样本方差为s^2=1.143^2,求μ的置信度为0.95的置信区间.”相关问题

  • 第1题：

    食盐中碘的含量服从正态分布，从中抽取容量n=11的样本，测得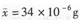，s=6.8×10-6g，则碘含量的方差σ2的置信度为95%的置信区间是( )。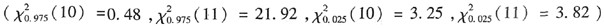

    A．[21.09×10-12，121.05×10-12]

    B．[21.09×10-12，142.28×10-12]

    C．[22.58×10-12，121.05×10-12]

    D．[22.58×10-12，142.28×10-12]


    正确答案：D
    解析：利用χ2(n-1)分布可得σ2的(1-α)的置信区间为：

  • 第2题：

    设总体X~N(u,σ2)，u与σ2均未知，x1,x2,...,x9为其样本，样本方差，则u的置信度为0. 9的置信区间是：


    答案：C
    解析：

  • 第3题：

    采用包装机包装食盐，要求500g装一袋，已知标准差σ= 3g，要使食盐每包平均重量的95%置信区间长度不超过4.2g，样本量n至少为（ ）。
    A. 4 B. 6 C. 8 D. 10


    答案：C
    解析：

  • 第4题：

    已知一批零件的长度X(单位：cm)服从正态分布N(μ，1)，从中随机地抽取16个零件，得到长度的平均值为40(cm)，则μ的置信度为0.95的置信区间是_______.(注：标准正态分布函数值φ(1.96)=0.975，φ(1.645)=0.95.)


    答案：1、(39.51，40.49).
    解析：
    区间估计不是经常考的一个考点，一般都考单个正态总体方差已知条件下，求期望值μ的置信区间问题，置信区间为：，其中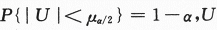～N(0，1).　　现题给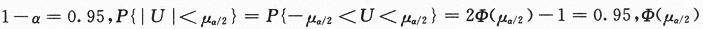=0.975，查得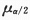=1.96.将σ=1，n=16,=40，代入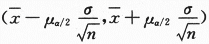得置信区间

  • 第5题：

    设总体X～N(u，σ2），基于来自总体X的容量为16的简单随机样本，测得样本均值x= 31.645，样本方差S2=0.09，则总体均值μ的置信度为0.98的置信区间为( )。




    A.(30.88, 32.63)

    B.(31.45, 31.84)

    C.(31.62, 31.97)

    D.(30.45, 31.74)

    答案：B
    解析：

  • 第6题：

    设总体X～N(u，σ2），基于来自总体X的容量为16的简单随机样本，测得样本均值图.png= 31.645，样本方差S2=0.09，则总体均值μ的置信度为0.98的置信区间为()。




    A.(30.88, 32.63)

    B.(31.45, 31.84)

    C.(31.62, 31.97)

    D.(30.45, 31.74)

    答案：B
    解析：

  • 第7题：

    总体平均数为”，方差U2的正态分布，则容量为，z的样本平均数分布服从


    答案：B
    解析：
    首先根据样本均值的抽样分布特点，当总体为正态分布，方差已知的时候，抽自该总体的样本容量为n的全部简单随机样本，其所有样本均值服从正态分布，且平均数与总体的平均数相同，方差为母总体方差与样本容量的商。

  • 第8题：

    袋装水泥重量X～N（49.85Kg，σ2），经调整包装机后随机抽取20袋，测得均值为49.96Kg，为比较改进前后的效果需做什么假设检验（）

    • A、Z检验
    • B、t检验
    • C、F检验
    • D、x2检验

    正确答案:B

  • 第9题：

    某车间用1台包装机装葡萄糖，额定标准为每袋净重0.5kg，包装机正常工作称糖服从正态分布，且根据长期经验知其标准方差Ϭ=0.015。某天，为检验包装机工作是否正常，随机抽取9包糖，检测它们的称重（单位：kg）平均值为：0.511。问这天包装机工作是否正常？（取α=0.05）


    正确答案: 1）设：H0：X0=X；（无显著差异，机器工作正常）
    H.A：X0≠X（有显著差异，机器工作不正常）
    2）σx=0.015÷3=0.005
    3）u=（0.5110.5）÷0.005=2.2
    由于，u=2.2＞u=1.96，
    所以，检验的样本与标准之间有显著的差异，即该机器工作不正常。

  • 第10题：

    问答题
    某车间用1台包装机装葡萄糖，额定标准为每袋净重0.5kg，包装机正常工作称糖服从正态分布，且根据长期经验知其标准方差Ϭ=0.015。某天，为检验包装机工作是否正常，随机抽取9包糖，检测它们的称重（单位：kg）平均值为：0.511。问这天包装机工作是否正常？（取α=0.05）

    正确答案： 1）设：H0：X0=X；（无显著差异，机器工作正常）
    H.A：X0≠X（有显著差异，机器工作不正常）
    2）σx=0.015÷3=0.005
    3）u=（0.5110.5）÷0.005=2.2
    由于，u=2.2＞u=1.96，
    所以，检验的样本与标准之间有显著的差异，即该机器工作不正常。
    解析： 暂无解析

  • 第11题：

    单选题
    某品牌袋装白糖每袋重量的标准是500±5克。为了检验该产品的重量是否符合标准，现从某日生产的这种白糖中随机抽查10袋，测得平均每袋重量为498克。下列说法中错误的是（）
    A

    样本量为10

    B

    抽样误差是2克

    C

    样本平均每袋重量是估计量

    D

    点估计值为498克


    正确答案： C
    解析： 暂无解析

  • 第12题：

    填空题
    总体为正态分布、方差σ2未知。 样本量n = 20、样本的平均值为χ、标准差为 S ，当置信水平 为1-α时，总体均值μ的置信区间为（）。

    正确答案： χ±tα/2(20-1)S/√20
    解析： 暂无解析

  • 第13题：

    设总体X～N（μ,σ^2）,其中σ^2未知,^2s=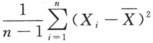,样本容量n,则参数μ的置信度为1－a的置信区间为().



    答案：D
    解析：
    因为σ^2未知，所以选用统计量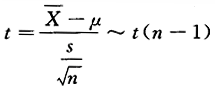，故μ的置信度为1-α的置信区间为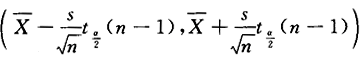，选(D).

  • 第14题：

    关于中心极限定理，下列说法正确的是（ ）。
    A.多个随机变量的平均值（仍然是一个随机变量）服从或近似服从正态分布
    B. n个相互独立同分布随机变量，其共同分布不为正态分布或未知，但其均值μ和方差σ2都存在，则在n相当大的情况下，样本均值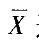
    近似服从正态分布N(μ, σ2/n)
    C.无论什么分布（离散分布或连续分布，正态分布或非正态分布），其样本均值的分布总近似于正态分布
    D.设n个分布一样的随机变量，假如其共同分布为正态分布N(μ, σ2)则样本均值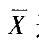仍为正态分布，其均值不变仍为μ，方差为 σ2/n


    答案：B
    解析：
    AC两项成立的前提条件是多个随机变量必须相互独立且同分布；D项要求这些随机变量相互独立。

  • 第15题：

    采用包装机包装食盐，要求500g装一袋，已知标准差σ=3g，要使食盐每包平均重量的95%置信区间长度不超过2g，样本量n至少为（ ）。已知u0.975=1.96, u0.95 = 1. 64。 A. 10 B. 24 C. 35 D. 70


    答案：C
    解析：

  • 第16题：

    设X～N（μ,σ^2）,其中σ^2已知,μ为未知参数,从总体X中抽取容量为16的简单随机样本,且μ的置信度为0.95的置信区间中的最小长度为0.588,则σ^2=_______.


    答案：1、0.36
    解析：
    在σ^2已知的情况下，μ的置信区间为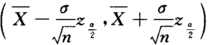，其中.于是有.

  • 第17题：

    某商场从一批袋装食品中随机抽取10袋，测得每袋重量(单位：克)分别为789，780，794，762，802，813，770，785，810，806，假设重量服从正态分布，要求在5％的显著性水平下，检验这批食品平均每袋重量是否为800克。
    选择的检验统计量是（）。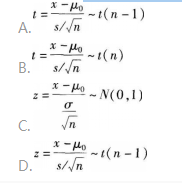


    答案：A
    解析：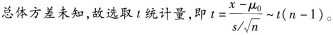

  • 第18题：

    某商场从一批袋装食品中随机抽取10袋，测得每袋重量（单位：克）分别为789．780，794，762，802，813，770，785，810，806，假设重量服从正态分布，要求在5%的显著性水平下，检验这批食品平均每袋重量是否为800克。

    根据上述资料请回答：
    假设检验的拒绝域是()。


    A.(- ∞,-zα/2］∪[zα/2, +∞)

    B.(- ∞,-tα/2］∪[tα/2, +∞), tα/2= tα/2(n)

    C.(- ∞,-tα/2］∪[tα/2, +∞), tα/2= tα/2(n-1)

    D.( tα，+∞)

    答案：C
    解析：

  • 第19题：

    某品牌袋装白糖每袋重量的标准是500±5克。为了检验该产品的重量是否符合标准，现从某日生产的这种白糖中随机抽查10袋，测得平均每袋重量为498克。下列说法中错误的是（）

    • A、样本量为10
    • B、抽样误差是2克
    • C、样本平均每袋重量是估计量
    • D、点估计值为498克

    正确答案:B

  • 第20题：

    总体为正态分布、方差σ2未知。 样本量n = 20、样本的平均值为χ、标准差为 S ，当置信水平 为1-α时，总体均值μ的置信区间为（）。


    正确答案:χ±tα/2(20-1)S/√20

  • 第21题：

    袋装水泥重量X～N（49.85Kg，σ2），经调整包装机后随机抽取20袋，测得均值为49.96Kg，为比较改进前后的效果需做什么假设检验（）

    • A、Z检验
    • B、t检验
    • C、F检验
    • D、χ2检验

    正确答案:B

  • 第22题：

    单选题
    某厂自动包装机包装味精，每500g装一袋，已知标准差d=2g,要使每包味精的平均重量的95％置信区间不超过4g，样本量n至少为（）。
    A

    4

    B

    6

    C

    8

    D

    10


    正确答案： D
    解析： 根据置信区间的定义可以知道。

  • 第23题：

    问答题
    从某种型号的晶体管中抽取10件做样本测量其寿命，测得寿命的标准差为s＝45（小时），设这批晶体管的寿命服从于正态分布N（μ，σ2），其中μ，σ2均为未知，求σ2的置信度为0.975的单侧置信上限。

    正确答案：
    依题意可知n=10,s2=452=2025,1-α=0.025,(n-1)S2/σ2~χ2(n-1),查χ2分布表,χ1-α2(n-1)=χ0.0252(9)=2.700。
    当μ未知时,σ2的置信度为1-α的单侧置信区间为(0,(n-1)S2/[χ1-α2(n-1)]),所以σ2的置信度为0.975的单侧置信区间上限为(n-1)s2/[χ1-α2(n-1)]=9×2025/2.7=6750。
    解析： 暂无解析

相关内容