安徽省马鞍山市中加学校2020届高三数学第三次模拟试题理(含解析)

二、填空题(本大题共15小题，每小题2分，共30分)

请在每小题的空格中填上正确答案。错填、不填均无分。

11．将三个不同的球随机地放入三个不同的盒中，则出现两个空盒的概率为______．

正确答案：

11.1/9

三、计算题（本大题共2小题，每小题8分，共16分）

26．某种灯管按要求使用寿命超过1000小时的概率为0.8，超过1200小时的概率为0.4，现有该种灯管已经使用了1000小时，求该灯管将在200小时内坏掉的概率。

正确答案：

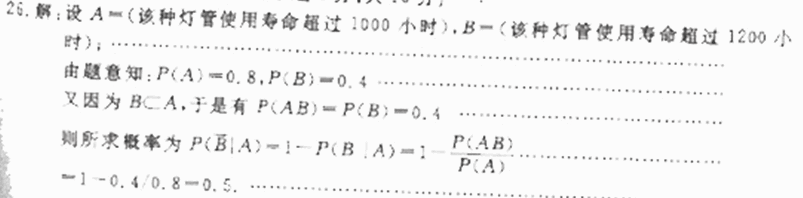
一、单项选择题(本大题共30小题，每小题1分，共30分)

在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。错选、多选或未选均无分。

1.清代由盛转衰的时期是( )

A.乾隆朝后期 B.道光朝后期

C.同治帝时期 D.光绪帝时期

正确答案：A

三、简答题(本大题共5小题，每小题6分，共30分)

41.近代中国工人阶级的特点。

正确答案：
一般无产阶级的优点：
(1)与最先进的生产方式相联系，
(2)富于组织性纪律性，
(3)没有私人占有的生产资料。
独特的优点：
(1)整个阶级基本是最革命的；
(2)具有坚强的斗争性和彻底的革命性；
(3)大部分出身农民，与农民有天然的联系，便于结成亲密的工农联盟。
(4)地区和行业的集中，便于组织。

四、论述题(本大题共2小题，每小题10分，共20分)

46．半殖民地半封建社会的主要矛盾及其关系。

正确答案：

在鸦片战争前中国社会是封建社会，是一个主权独立的国家。而1840年至1949年的近代中国社会性质是半殖民地半封建。帝国主义对中国的侵略是近代中国贫穷落后的总根源。

    近代中国半殖民地半封建社会的主要矛盾就是帝国主义和中华民族的矛盾，封建主义和人民大众的矛盾，而帝国主义与中华民族的矛盾则是最主要的矛盾。

    近代中国社会的基本特点：①中国形式上是独立的，但实际上失去了主权独立和领土完整。②中国的封建势力和帝国主义相勾结，构成统治中国的社会和政治基础。 ③帝国主义在中国划分势力范围，实行分裂剥削政策，造成中国实际上长期不统一，政治、经济、文化的发展极端不平衡。④民族资本主义工商业有了某些发展，但很微弱，没有成为中国社会经济的主要形式。⑤由于帝国主义和封建主义的压迫，中国人民尤其是占人口80%以上的农民极端贫困化。⑥封建主义统治者顽固地推行以儒家为中心的思想文化，禁锢着人们的思想；帝国主义则宣扬与推行殖民主义思想文化，麻痹中国人民的斗志。

    近代中国半殖民地半封建社会的主要矛盾和基本特点，构成了近代中国的基本国情。认清近代中国的基本国情，乃是认清一切革命问题的基本依据。近代中国半殖民地半封建社会的性质的主要矛盾，规定了：近代中国民族民主革命的性质是资产阶级民主革命；主要对象是外国帝国主义和本国封建主义；主要任务是反对外国帝国主义，求得民族的独立和反对本国封建主义的统治，求得人民的解放；革命的动力应该包括工人阶级、农民阶级、小资产阶级和民族资产阶级。

安徽省马鞍山市中加学校 2020 届高三数学第三次模拟试题理（含解析）一.选择题：本大题共 12个小题 ,每小题 5分,共 60分.在每小题给出的四个选项中，只有项是符合题目要求的 .已知集合，，则集合中元素的个数为（）A. B. C. D.【答案】 C 【解析】由题得，集合，所以 .集合中元素的个数为 3.故选 C.已知命题：，则命题为（）A. ， B. ，C. ， D. ，【答案】 D【解析】全称命题的否定是特称命题，则：若命题：，则命题为， .本题选择D选项已知复数（为虚数单位），则复数在复平面内对应的点位于（）A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限【答案】 D【解析】结合复数的运算法则可得：，即复数在复平面内对应的点位于第四象限 .本题选择D选项.已知双曲线：的一个焦点为，则双曲线的渐近线方程为（）A. B. C. D.【答案】 A【解析】由题意得，，则，即 .所以双曲线的渐近线方程为，即 .故选 A.2020 年 8月 1日是中国人民解放军建军 90周年，中国人民银行为此发行了以此为主题的金银纪念币 . 如图所示是一枚 8 克圆形金质纪念币，直径，面额100 元. 为了测算图中军旗部分的面积，现用 1 粒芝麻向硬币内投掷 100 次，其中恰有 30 次落在军旗内，据此可估计军旗的面积大约是（）A. B. C. D.【答案】 B【解析】利用古典概型近似几何概型可得，芝麻落在军旗内的概率为，设军旗的面积为S,由题意可得：.本题选择B选项下列函数中，与函数的定义域 . 单调性与奇偶性均一致的函数是（）A. B. C. D.【答案】 D【解析】函数为奇函数，且在 R 上单调递减，对于A,是奇函数，但不在 R上单调递减；对于B,是奇函数，但在 R上单调递增；对于 C，对于D,画出函数图象可知函数是奇函数，且在R上单调递减，故选 D.如图是一个空间几何体的正视图和俯视图，则它的侧视图为（）A. B.C. D.【答案】 A【解析】由正视图和俯视图可知，该几何体是一个圆柱挖去一个圆锥构成的，结合正视图的宽及俯视图的直径可知其侧视图为 A.故选 A.点睛：思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽 . 由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整 .设，则，的大小关系为（）A. B.C. D.【答案】 A【解析】由题意得， . 得，而 .所以，即 1.又.故.选 A.执行如图所示的程序框图，则输出的值为（）A. B. C. D.【答案】 B 【解析】由框图可知， . 故选 B.将函数的图象向左平移个单位，再把所有点的横坐标伸长到原来的 2 倍，得到函数的图象，则下列关于函数的说法错误的是（）A. 最小正周期为 B. 图象关于直线对称C. 图象关于点对称 D. 初相为【答案】 C【解析】易求得，其最小正周期为，初相位，即A，D 正确，而.故函数的图象关于直线对称，即B项正确，故C错误选 C.抛物线有如下光学性质：过焦点射出的光线经抛物线反射后平行于抛物线的对称轴；反之，平行于抛物线的对称轴的入射光线经抛物线反射后必过抛物线的焦点. 已知抛物线的焦点为，一条平行于轴的光线从点射出，经过抛物线上的点反射后，再经抛物线上的另一点射出，则直线的斜率为（A. B. C. D.【答案】 B【解析】令，代入可得，即 . 由抛物线的光学性质可知，直线经过焦点，所以 .故选 B.点睛：抛物线的光学性质：从抛物线的焦点发出的光线或声波在经过抛物线周上反射后 , 反射光线平行于抛物线的对称轴 .已知的内角，，的对边分别是，，且，若，则的取值范围为（）A. B. C. D.【答案】 B【解析】由题意可得： ,且，据此可得：，即：，据此有：，当且仅当时等号成立；三角形满足两边之和大于第三边，则，综上可得：的取值范围为 .本题选择B选项点睛： 1在解三角形的问题中，三角形内角和定理起着重要作用，在解题时要注意根据这个定理确定角的范围及三角函数值的符号，防止出现增解或漏解2 正、余弦定理在应用时，应注意灵活性，尤其是其变形应用时可相互转化如a2 = b2 + c22bccos A可以转化为sin2 A = sin2 B+ sin 2 C 2sin Bsin Ceos A 利用这些变形可进行等式的化简与证明.二. 填空题：本题共 4 小题，每小题 5 分，共 20 分设，则等于 .【答案】 30【解析】，则，故答案为 .向如图所示的边长为的正方形区域内任投一点，则该点落入阴影部分的概率为答案】【解析】由题意阴影部分的面积为，所以所求概率为设满足约束条件，其中目标函数的最大值为12，则的最小值为 .【答案】【解析】试题分析：不等式组表示的平面区域如下图中的阴影区域所示，根据图形可知，目标函数在点处取得最大值，即，所以，则，当且仅当，即时等号成立 .考点： 1、线性规划； 2、均值定理 . 【方法点晴】线性规划问题一般有截距型问题、斜率型问题、距离型问题、含参数问题、实际应用问题等几类常见的考法 . 这里重点考查截距型问题，即转化为，当时，直线在轴的截距越大则值越大，反之当时，直线在轴的截距越大则值越小，掌握这一结论便可以求出目标函数最优解 .中国古代数学经典九章算术中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形

一、单项选择题(本大题共20小题，每小题1分，共20分)

在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。错选、多选或未选均无分。

1.贯穿《寡人之于国也》始终的论题是( )

A.民何以才能够加多 B.小恩小惠不是王道

C.实行王道的根本措施 D.实行王道的正确态度

正确答案：A
本文阐述了孟子的王道思想和实行王道的根本措施，全文围绕“民不加多”和如何使“民加多”的问题展开论述。

二、多项选择题(本大题共5小题，每小题2分，共10分)

在每小题列出的五个备选项中至少有两个是符合题目要求的，请将其代码填写在题后的括号内。错选、多选、少选或未选均无分。

21.下列文章，采用寓言形式的有( )

A.《秋水》 B.《吃饭》 C.《蚂蚁大战》

D.《婴宁》 E.《种树郭橐驼传》

正确答案：AE

三、词语解释题(本大题共10小题，每小题1分，共10分)

26.直不百步耳，是亦走也

直：

正确答案：

多项选择题

第51-55小题，每小题2分，共10分。下列每题给出的四个选项中，至少有两个选项是符合题目要求的。请在答题卡上将所选项的字母涂黑。多选、少选或错选均不得分。

下列属于无效民事行为的有( )。

A．无民事行为能力人实施的民事行为

B．恶意串通损害他人利益的民事行为

C．违反社会公共利益的民事行为

D．以合法形式掩盖非法目的的民事行为

正确答案：ABCD
解析：本题考核无效民事行为的种类。

多项选择题

第21-25小题，每小题2分，共10分。下列每题给出的四个选项中，至少有两个选项是符合题目要求的。请在答题卡上将所选项的字母涂黑。多选、少选或错选均不得分。

在下列情形中，应视为不法侵害已经终止的是______。

A．不法侵害已经完结

B．不法侵害人自动中止侵害

C．不法侵害人已被制服

D．不法侵害人已经丧失继续侵害的能力

正确答案：ABCD
解析：本题考查刑法中所规定的不法侵害已经终止的情况，题目中所给的情形均应视为不法侵害行为终止。

安徽省马鞍山市中加学校2020届高三数学第三次模拟试题理(含解析)

更多 “安徽省马鞍山市中加学校2020届高三数学第三次模拟试题理(含解析)” 相关考题

相关内容

最新试卷

热门试卷