2022《空间向量》考题总汇
判断折线段方向的方法是根据形成这条折线段上每条线段所在()的结果的符号判断。
A.向量的和
B.向量的差
C.向量的叉积
D.向量的点积
已知向量a,b,c是三个具有公共起点的非零向量,且|a|=2|b|=2,又a·b=-1, 〈a-c,b-c 〉=π/3 ,则当|a-c|=7时,向量a与c的夹角是____.
患者男性，56岁，常规检查心电图后，还做了心电向量图检查。心电向量图与心电图的关系是A、空间心电向量投影在平面上形成心电图
B、空间心电向量第1次投影在平面上形成心电图，第2次投影在直线上形成心电向量图
C、空间心电向量第2次投影在直线上形成心电图
D、空间心电向量第1次投影在平面上形成平面心电向量图，平面心电向量图第2次投影在导联轴上形成心电图
E、心电向量图和心电图均是记录随时间而变化的电压曲线
关于心电向量图的表述，不正确的是A、分析额面、侧面和水平面心电向量图可对空间向量环进行描述
B、临床上通常描记的心电向量图是一个平面向量图
C、心电向量图描记的是一个环形图
D、其纵坐标反映的是向量在该坐标上的强弱
E、其横坐标反映的是时间
关于心电图产生原理的表述，不正确的是A、心电图是额面和横面心电向量环投影在导联轴上而形成
B、心电图记录的是两个电极之间电位差随时间变化的曲线
C、常规12导联心电图主要反映额面心电向量的变化
D、心电图纵坐标反映向量的强弱变化
E、心电图横坐标反映的是时间变化
问题 2 答案：E
问题 3 答案：C
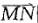同向的单位向量可表示为：
A.{-4,-7,4}
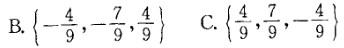D.{-4,-7,-4}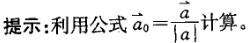
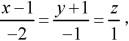则直线：
(A)过点(1,-1,0)，方向向量为2i + j-k
(B)过点(1,-1,0)，方向向量为2i - j + k
(C)过点(-1,1,0)，方向向量为-2i - j + k
(D)过点(-1,1,0)，方向向量为2i + j - k
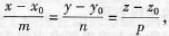
此方程称为直线的对称式方程， 如设参数t如下：
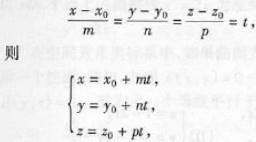此方程组称为直线的参数式方程。
空
定义：与平面向量运算一样，空间向量的加法、减法与数乘向量运算如下 ；（2）运算律： 加法交换律：； 加法结合律：； 数乘分配律：；用行路法分解向量，会比较简单，容易理解。 具体操作方法：假设自己行路，绕路行，如果行路方向与向量方向一致，则向量为正，否则为负；把行路经过的向量相加即为该向量分解的结果。（4）向量的数量积： 已知向量和轴，是上与同方向的单位向量，作点在上的射影，作点在上的射影，则叫做向量在轴上或在上的正射影. 可以证明的长度（5）空间向量数量积的性质： （1）（2）（3）（6）空间向量数量积运算律： （1） （2）（交换律）（3）（分配律）
在空间四边形OABC中， eq o(OA,sup6()eq o(AB,sup6()eq o(CB,sup6()等于( 答案：C；解析：eq o(OA,sup6()eq o(AB,sup6()eq o(CB,sup6()Oeq o(B,sup6()eq o(CB,sup6()eq o(OB,sup6()eq o(BC,sup6()eq o(OC,sup6().)Aeq o(OA,sup6() Beq o(AB,sup6() C eq o(OC,sup6() Deq o(AC,sup
()如图所示，已知平行六面体OABCOABC，eq o(OA,sup6()a，eq o(OC,sup6()c，eq o(OO,sup6()b，D是四边形OABC的中心，则( 答案：D；解析：eq o(OD,sup6()eq o(OO,sup6()eq o(OD,sup6()eq o(OO,sup6()eq f(1,2)eq o(OB,sup6()eq o(OO,sup6()eq f(1,2)(eq o(OA,sup6()eq o(OC,sup6()eq f(1,2)abeq f(1,2)c.)A.eq o(OD,sup6()abc B.eq o(OD,sup6()beq f(1,2)aeq f(1,2)c C.eq o(OD,sup6()eq f(1,2)abeq f(1,2)c D.eq o(OD,sup6()eq f(1,2)abeq f(1,2)
如图所示，已知正三棱锥ABCD的侧棱长和底面边长都是a，点E，F，G是AB，AD，DC上的点，且AEEBAFFDCGGD12，求下列向量的数量积：(1)Aeq o(D,sup6()Deq o(B,sup6()；(2)Aeq o(D,sup6()Beq o(C,sup6()；(3)Geq o(F,sup6()Aeq o(C,sup6()；(4)Eeq o(F,sup6()Beq o(C,sup6(). 答案：eq f(1,2)a2，0，eq f(2,3)a2，eq f(1,6)a2；解析：(1)|Aeq o(D,sup6()|a，|eq o(BD,sup6()|a，Aeq o(D,sup6()，Deq o(B,sup6()120，所以Aeq o(D,sup6()Deq o(B,sup6()|eq o(AD,sup6()|Deq o(B,sup6()|cos 120eq f(1,2)a2.(2)因为Beq o(C,sup6()Aeq o(C,sup6()Aeq o(B,sup6()，所以Aeq o(D,sup6()Beq o(C,sup6()Aeq o(D,sup6()(Aeq o(C,sup6()Aeq o(B,sup6()Aeq o(D,sup6()Aeq o(C,sup6()Aeq o(D,sup6()Aeq o(B,sup6()，又因为|Aeq o(D,sup6()|a，|eq o(BC,sup6()|a，Aeq o(D,sup6()，Aeq o(C,sup6()Aeq o(D,sup6()，Aeq o(B,sup6()60，所以Aeq o(D,sup6()Beq o(C,sup6()eq f(1,2)a2eq f(1,2)a20.
因为点F，G是AD，DC上的点，所以Geq o(F,sup6()eq f(2,3)eq o(CA,sup6()eq f(2,3)Aeq o(C,sup6()，所以Geq o(F,sup6()Aeq o(C,sup6()eq f(2,3)eq o(AC2,sup6()，因为eq o(AC2,sup6()a2，所以Geq o(F,sup6()Aeq o(C,sup6()eq f(2,3)a2.
因为点E，F分别是AB，AD上的点，所以Eeq o(F,sup6()eq f(1,3)Beq o(D,sup6()，所以Eeq o(F,sup6()Beq o(C,sup6()eq f(1,3)Beq o(D,sup6()Beq o(C,sup6()，结合图形可知Beq o(D,sup6()，Beq o(C,sup6()60，所以Eeq o(F,sup6()Beq o(C,sup6()eq f(1,3)Beq o(D,sup6()Beq o(C,sup6()eq f(1,3)aacos 60eq f(1,6)a
如图所示，在正方体ABCDA1B1C1D1中，下列各式中运算结果为向量eq o(AC1,sup6()的是( 答案：D；解析：(eq o(AB,sup6()eq o(BC,sup6()eq o(CC1,sup6()eq o(AC,sup6()eq o(CC1,sup6()eq o(AC1,sup6()；(eq o(AA1,sup6()eq o(A1D1,sup6()eq o(D1C1,sup6()eq o(AD1,sup6()eq o(D1C1,sup6()eq o(AC1,sup6()；(eq o(AB,sup6()eq o(BB1,sup6()eq o(B1C1,sup6()eq o(AB1,sup6()eq o(B1C1,sup6()eq o(AC1,sup6()；(eq o(AA1,sup6()eq o(A1B1,sup6()eq o(B1C1,sup6()eq o(AB1,sup6()eq o(B1C1,sup6()eq o(AC1,sup6().)(eq o(AB,sup6()eq o(BC,sup6()eq o(CC1,sup6()； (eq o(AA1,sup6()eq o(A1D1,sup6()eq o(D1C1,sup6()； (eq o(AB,sup6、()eq o(BB1,sup6()eq o(B1C1,sup6()； (eq o(AA1,sup6()eq o(A1B1,sup6()eq o(B1C1,sup6().A B C D在四棱锥PABCD中，底面ABCD是正方形，E为PD中点，若eq o(PA,sup6()a，eq o(PB,sup6()b，eq o(PC,sup6()c
.试用a，b，c表示向量eq o(BE,sup6(). 答案：eq f(1,2)aeq f(3,2)beq f(1,2)c；解析：eq o(BE,sup6()eq f(1,2)(eq o(BD,sup6()eq o(BP,sup6()eq f(1,2)(eq o(、BA,sup6()eq o(BC,sup6()eq o(BP,sup6()eq f(1,2)(eq o(PA,sup6()eq o(PB,sup6()eq o(PC,sup6()eq o(PB,sup6()eq o(PB,sup6()eq f(1,2)eq o(PA,sup6()eq f(3,2)eq o(PB,sup6()eq f(1,2)eq o(PC,sup6()eq f(1,2)aeq f(3,2)beq f(1,2)c. 在空间四边形ABCD中，Aeq o(B,sup6()Ceq o(D,sup6()Beq o(C,sup6()Aeq o(D,sup6()Ceq o(A,sup6()
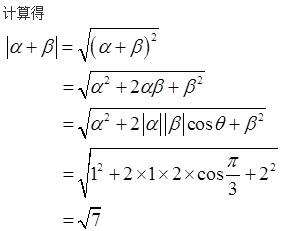
二、考题解析
【教学过程】
(一)引入课题
(课件)引入：有一块质地均匀的正三角形面的钢板，重500千克，顶点处用与对边成60度角，大小200千克的三个力去拉三角形钢板，问钢板在这些力的作用下将如何运动?这三个力至少多大时，才能提起这块钢板?
提问：我们研究的问题是三个力的问题，力在数学中可以看成是什么?这三个向量和以前我们学过的向量有什么不同?
(学生得出：这是三个向量不共面)
追问：不共面的向量问题能直接用平面向量来解决么?解决这类问题需要空间向量的知识。这节课我们就来学习空间向量。
(二)探求新知
1.生活实例感知
空间向量我们随处可见，同学们能不能举出一些例子?(学生举例)
再演示(课件)几种常见的空间向量身影。(常见的高压电线及支架所在向量，长方体中的三个不共线的边上的向量，平行六面体中的不共线向量)
2.类比概念形成
接下来我们我们就来研究空间向量的知识、概念和特点，空间向量与平面向量既有联系又有区别，我们将通过类比的方法来研究空间向量，首先我们复习回顾一下平面向量的知识。师生一起回忆平面向量概念、向量的模、零向量、单位向量、相反向量、相等向量等，引导学生理解空间向量就是把向量放到空间中了，请同学们给空间向量下个定义，
(学生：在空间中，既有大小又有方向的量)
现在请同学们阅读教材，找出空间向量的相关定义，用类比的方法记忆并填写课件的表格：
3.类比运算定律形成
在数学中引入一种量以后，一个很自然的问题就是研究它们的运算，空间向量的运算我们也采用与平面向量类比的方法，那么我们首先来复习回顾一下平面向量的加减运算。(课件)复习回顾：(找学生回答)
提问：同学课下的复习很好。我们先来探讨这样一个问题：对于两个向量来说空间向量和平面向量有没有区别?
学生探讨研究：平面向量可在同一平面内平移，而空间向量也可在空间中平移。平移后的向量与原向量是同一向量。由此得出：空间任意两个向量都可转化为共面向量。
引导学生得出任意的空间中的两个向量的运算与平面向量的结论一致，这样我们就能够定义空间向量的加法和减法运算。
同样地，用类比(表格)形式对比给出空间向量的相关定义，采用填空形式填写下列有关内容：(课件)
(三)巩固提高
课堂练习例1.
(四)小结作业
这节课，我们在平面向量的基础上学习了平面向量，接下来给同学们两分钟的时间总结一下这节课的主要内容。(学生总结)
通过这节课的学习，我们学会了空间向量的有关概念，加减运算及其运算律以及空间向量的加减运算在空间几何体中的应用。
作业：(1)课后练习题1、2;
(2)思考题：共始点的两个不共线向量的加法满足平行四边形法则。和向量是平行四边形的对角线。请问，共始点的三个不共面的向量满足什么法则?和向量是什么向量?
【板书设计】
【答辩题目解析】
1.平行向量是如何定义的?
2.空间向量在高中数学中具有怎样的地位和作用?
2、用空间向量处理某些立体几何问题，可以为学生提供新的视角。在空间特别是空间直角坐标系中引入空间向量，可以为解决三维图形的形状、大小及位置关系的几何问题增加一种理想的代数工具，从而提高学生的空间想象能力和学习效率。
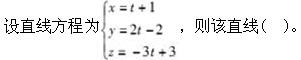
B.过点(-1，2，-3)，方向向量为-i-2j+3k
C.过点(1，2，-3)，方向向量为i-2j+3k
D.过点(1，-2，3)，方向向量为-i-2j+3k
