填空题已知空间向量，则2a＋b＝____．

题目
填空题
已知空间向量，则2a＋b＝____．
相似考题

1.2A＋B=2C已知反应某一瞬间,rA=12.72mol·dm－3·h－1,则rB=(),rC=()。

2.已知向量a,b,c是三个具有公共起点的非零向量,且|a|=2|b|=2,又a·b=-1, 〈a-c,b-c 〉=π/3 ,则当|a-c|=7时,向量a与c的夹角是____.

3.已知平面向量a=（1，1），b=（1，-l），则两向量的夹角为（ ）A.AB.BC.CD.D

4.已知2a+b=3c，3a-b=2c，a与b的关系是A．a=6B．a=2bC．a=-bD．a=b

更多“已知空间向量，则2a＋b＝____．”相关问题

  • 第1题：

    设向量组Ⅰ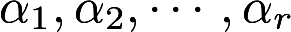可由向量组Ⅱ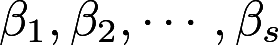:线性表示,下列命题正确的是( )



    A.若向量组Ⅰ线性无关,则r≤s
    B.若向量组Ⅰ线性相关,则r大于s
    C.若向量组Ⅱ线性无关,则r≤s
    D.若向量组Ⅱ线性相关,则r小于s

    答案：A
    解析：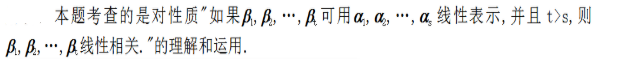

  • 第2题：

    已知向量a、b、c都是单位向量，且满足a+b+c=0．则a·b+b·c+c·a=( )。



    答案：C
    解析：
    对a+b+c=0平方，然后计算即可得到解

  • 第3题：

    已知｜a｜=1，｜b｜=6，a?(b-a)=2，则向量a与b的夹角是(　　).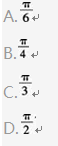


    答案：C
    解析：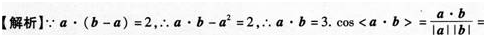

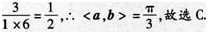
  • 第4题：

    已知向量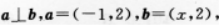则χ=( )

    A.4
    B.-8
    C.8
    D.-4

    答案：A
    解析：
    【考情点拨】本题主要考查的知识点为向量的垂直． 【应试指导】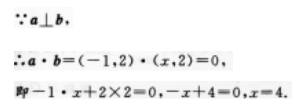

  • 第5题：

    高中数学《空间向量》



    二、考题解析
    【教学过程】
    (一)引入课题
    (课件)引入：有一块质地均匀的正三角形面的钢板，重500千克，顶点处用与对边成60度角，大小200千克的三个力去拉三角形钢板，问钢板在这些力的作用下将如何运动?这三个力至少多大时，才能提起这块钢板?
    提问：我们研究的问题是三个力的问题，力在数学中可以看成是什么?这三个向量和以前我们学过的向量有什么不同?
    (学生得出：这是三个向量不共面)
    追问：不共面的向量问题能直接用平面向量来解决么?解决这类问题需要空间向量的知识。这节课我们就来学习空间向量。
    (二)探求新知
    1.生活实例感知
    空间向量我们随处可见，同学们能不能举出一些例子?(学生举例)
    再演示(课件)几种常见的空间向量身影。(常见的高压电线及支架所在向量，长方体中的三个不共线的边上的向量，平行六面体中的不共线向量)
    2.类比概念形成
    接下来我们我们就来研究空间向量的知识、概念和特点，空间向量与平面向量既有联系又有区别，我们将通过类比的方法来研究空间向量，首先我们复习回顾一下平面向量的知识。师生一起回忆平面向量概念、向量的模、零向量、单位向量、相反向量、相等向量等，引导学生理解空间向量就是把向量放到空间中了，请同学们给空间向量下个定义，
    (学生：在空间中，既有大小又有方向的量)
    现在请同学们阅读教材，找出空间向量的相关定义，用类比的方法记忆并填写课件的表格：
    3.类比运算定律形成
    在数学中引入一种量以后，一个很自然的问题就是研究它们的运算，空间向量的运算我们也采用与平面向量类比的方法，那么我们首先来复习回顾一下平面向量的加减运算。(课件)复习回顾：(找学生回答)
    提问：同学课下的复习很好。我们先来探讨这样一个问题：对于两个向量来说空间向量和平面向量有没有区别?
    学生探讨研究：平面向量可在同一平面内平移，而空间向量也可在空间中平移。平移后的向量与原向量是同一向量。由此得出：空间任意两个向量都可转化为共面向量。
    引导学生得出任意的空间中的两个向量的运算与平面向量的结论一致，这样我们就能够定义空间向量的加法和减法运算。
    同样地，用类比(表格)形式对比给出空间向量的相关定义，采用填空形式填写下列有关内容：(课件)
    (三)巩固提高
    课堂练习例1.
    (四)小结作业
    这节课，我们在平面向量的基础上学习了平面向量，接下来给同学们两分钟的时间总结一下这节课的主要内容。(学生总结)
    通过这节课的学习，我们学会了空间向量的有关概念，加减运算及其运算律以及空间向量的加减运算在空间几何体中的应用。
    作业：(1)课后练习题1、2;
    (2)思考题：共始点的两个不共线向量的加法满足平行四边形法则。和向量是平行四边形的对角线。请问，共始点的三个不共面的向量满足什么法则?和向量是什么向量?
    【板书设计】



    【答辩题目解析】
    1.平行向量是如何定义的?
    2.空间向量在高中数学中具有怎样的地位和作用?


    答案：
    解析：
    1、平行向量又称共线向量，指的是方向相同或相反的两个非零向量。规定零向量和任何向量都平行。

    2、用空间向量处理某些立体几何问题，可以为学生提供新的视角。在空间特别是空间直角坐标系中引入空间向量，可以为解决三维图形的形状、大小及位置关系的几何问题增加一种理想的代数工具，从而提高学生的空间想象能力和学习效率。

  • 第6题：

    已知向量a=(-3，1)，b=(x，9)，若a⊥b，则x=( )。

    A.1
    B.2
    C.3
    D.4

    答案：C
    解析：
    向量a=(x1，y1)与b=(x2，y2)垂直，则x1x2+y1y2=0，代入数值可得x=3，选择C。

  • 第7题：

    向量空间模型


    正确答案: 将文档标识为由n个经过归一化处理的标引词构成的n维空间中的向量，该向量第k维的值（第k个分量）表示第k个标引词在文档中的权值。用户检索提问式也同样表示为一个n维向量。文档和检索提问式的RSV是这两个向量的标量乘积，RSV越大，文档和检索提问式的相关度便越大。

  • 第8题：

    若气相反应2A+B→P+S，则膨胀因子δA等于（）

    • A、1/2
    • B、-1/2
    • C、2
    • D、-2

    正确答案:B

  • 第9题：

    单选题
    心电向量图与心电图的关系是（　　）。
    A

    空间心电向量第1次投影在乎面上形成平面心电向量图，平面心电向量图第2次投影在导联轴上形成心电图

    B

    空间心电向量投影在平面上形成心电图

    C

    空间心电向量第2次投影在直线上形成心电图

    D

    空间心电向量第1次投影在平面上形成心电图，第2次投影在直线上形成心电向量图

    E

    心电向量图和心电图均是记录随时间而变化的电压曲线


    正确答案： B
    解析：
    空间心电向量第1次投影在额面、水平面和矢状面上形成平面心电向量图。额面心电向量图第2次投影在Ⅰ、Ⅱ、Ⅲ、aVR、aVL、aVF导联轴上形成肢体导联心电图，水平面心电向量图第2次投影在V1～V6导联轴上形成胸导联心电图。

  • 第10题：

    填空题
    实地址方式下，主存最低（）的存储空间用于中断向量表。向量号8的中断向量保存在物理地址（）开始的（）个连续字节空间；如果其内容从低地址开始依次是00H、23H、10H、F0H，则其中断服务程序的首地址是（）

    正确答案： 1KB,20H,4,F010H∶2300H
    解析： 暂无解析

  • 第11题：

    单选题
    已知3维列向量α，β满足αTβ=3，设3阶矩阵A=βαT，则（）。
    A

    β是A的属于特征值0的特征向量

    B

    α是A的属于特征值0的特征向量

    C

    β是A的属于特征值3的特征向量

    D

    α是A的属于特征值3的特征向量


    正确答案： D
    解析： 暂无解析

  • 第12题：

    单选题
    已知向量a＝（2，4），b＝（m，－1），且a⊥b，则实数m＝（　　）．
    A

    2

    B

    1

    C

    －1

    D

    －2


    正确答案： C
    解析：
    因为a⊥b，则a·b＝0，即2m＋4×（－1）＝0，解得m＝2．

  • 第13题：

    已知a、b均为非零向量，而｜a+b｜=｜a-b｜，则( )。

    A.a-b=0
    B.a+b=0
    C.a·b=0
    D.a×b=0

    答案：C
    解析：
    由a≠0，b≠0及｜a+b｜=｜a-b｜知(a+b)·(a+b)=(a-b)·(a-b)，即a·b=-a·b，所以a·b=0。

  • 第14题：

    已知两点A(4，0，5)和B(7，1，3)，则下面与AB方向相同的单位向量e为( )。




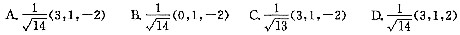    答案：A
    解析：

  • 第15题：

    已知四维列向量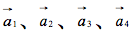线性无关，则下列向量组中线性无关的是



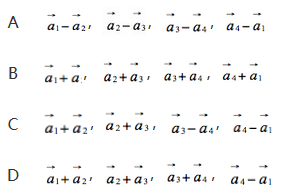    答案：
    解析：



  • 第16题：

    已知向量a=(3，4)，向量b=(0，-2)，则cos(a，b)的值为( )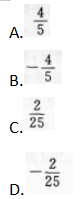


    答案：B
    解析：
    【考情点拨】本题主要考查e-j知识点为向量的夹角． 【应试指导】求cos〈a，b〉，可直接套用公式

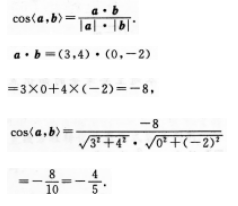
  • 第17题：

    已知基元反应2A+B=C+D，则反应的速率方程式为()。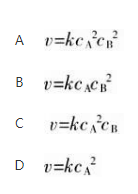



    答案：C
    解析：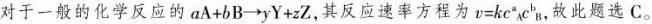

  • 第18题：

    已知数组A=[12；45]，则A（1，：）是指（）

    • A、第一行向量
    • B、第一列向量
    • C、整个数组
    • D、第一个元素

    正确答案:B

  • 第19题：

    实地址方式下，主存最低（）的存储空间用于中断向量表。向量号8的中断向量保存在物理地址（）开始的（）个连续字节空间；如果其内容从低地址开始依次是00H、23H、10H、F0H，则其中断服务程序的首地址是（）


    正确答案:1KB；20H；4；F010H∶2300H

  • 第20题：

    已知3维列向量α，β满足αTβ=3，设3阶矩阵A=βαT，则（）。

    • A、β是A的属于特征值0的特征向量
    • B、α是A的属于特征值0的特征向量
    • C、β是A的属于特征值3的特征向量
    • D、α是A的属于特征值3的特征向量

    正确答案:C

  • 第21题：

    单选题
    已知数组A=[12；45]，则A（1，：）是指（）
    A

    第一行向量

    B

    第一列向量

    C

    整个数组

    D

    第一个元素


    正确答案： C
    解析： 暂无解析

  • 第22题：

    填空题
    已知向量组（α1，α3），（α1，α3，α4），（α2，α3，）都线性无关，而（α1，α2，α3，α4）线性相关，则向量组（α1，α2，α3，α4）的极大无关组是____.

    正确答案： (α1,α3,α4)
    解析：
    向量组（α1，α2，α3，α4）线性相关，则其极大线性无关组最多含三个向量，又（α1，α3，α4）线性无关，故知（α1，α3，α4）为其极大线性无关组．

  • 第23题：

    问答题
    已知中断向量TINT=013H，中断向量地址指针IPTR=0111H，求中断向量地址。

    正确答案： 中断向量地址=(100010001B)<<9+(10011)<<2=88CCH
    解析： 暂无解析

相关内容