从0到9这10个数字中按次序任选两个不同的数,共有________种不同的取法。A．90B．100C．45D．36

题目

从0到9这10个数字中按次序任选两个不同的数,共有________种不同的取法。

A．90

B．100

C．45

D．36

相似考题

1.从1到9这9个正整数中,每次取出两个数使它们的和大于10,共有________种不同的取法。A．16B．20C．15D．10

2.从1、2、…、11这十一个自然数中，随机抽取五个不同的数，则这五个数的和为偶数的取法有多少种?(　)A、 220　　B、 226　　C、 231　　D、 236

3.从1、2、…、11这十一个自然数中，随机抽取五个不同的数，则这五个数的和为偶数的取法有多少种？（ ）A、 220B、 226C、 231D、 236

4.从0到9这10个数字中组成可重复的数对,则可以组成的数对共有________个。A．90B．100C．45D．36

更多“从0到9这10个数字中按次序任选两个不同的数,共有________种不同的取法。A.90B.100C.45D.36 ”相关问题

  • 第1题：

    在1,2,3…100这100个自然数中，取两个不同的数，使得它们的和是7的倍数，共有 ( )种不同的取法。

    A．700

    B．707

    C．697

    D．705


    正确答案：B
    [答案] B。解析：100÷7=14……2。在1～100中，按被7除的余数分为了类：余1与余2的各15个，余3、余4、余5、余6、整除的各14个。取两个不同的数，要使它们的和是7的倍数，必须是：一个余1一个余6，或一个余2一个余5，或一个余3一个余4，或两个都是整除。所以，不同的取法共有15×14+15×14+14×14+14×13÷2=707。

  • 第2题：

    从10双不同的鞋子中任取8只，若取出的鞋子中没有成对的，那么共有多少种不同的取法?（　　）
    A.45种
    B.2300种
    C.12500种
    D.11520种


    答案：D
    解析：
    第一步，从10双鞋子中取出8只，有四种方法；第二步，从选出的8双鞋子中每双拿出1只，有种方法。由乘法原理得：从10双鞋子中取出8只，且都不成对的方法总数有=11520种。

  • 第3题：

    从0、1、2、…、9这10个数中取出3个数，使其和是不小于10的偶数，不同的取法共有多少种？（）
    A. 50 B. 51 C. 52 D. 53


    答案：B
    解析：

  • 第4题：

    在九宫格内依次填入数字1～9，现从中任取两个数，要求取出的两个数既不在同一行也不在同一列，共有多少种不同取法？（ ）

    A. 9
    B. 18
    C. 36
    D. 45

    答案：B
    解析：
    任意从9个数字中选2个，共计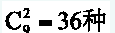

    任意选择其中一个位置的数值，选择第二个数时，必然有4个是同行同列，4个是非同行同列的，两者之间的比例为1:1，所以必然有18种是非同行同列的。正确答案为B。

  • 第5题：

    从1,2,…,9这九个数中,随机抽取3个不同的数,这3个数的和为偶数的取法有（ ）种

    A.36
    B.44
    C.60
    D.72
    E.90

    答案：B
    解析：

相关内容