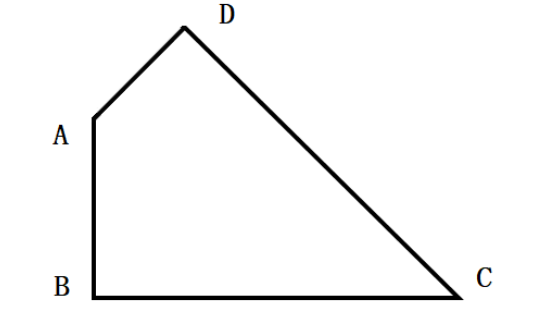
如图，已知一个四边形中边AD长为3cm，边BC长7cm；∠DAB＝135°，∠ABC=∠ADC=90°那么这个四边形的面积是（ ）cm2。

题目
如图，已知一个四边形中边AD长为3cm，边BC长7cm；∠DAB＝135°，∠ABC=∠ADC=90°那么这个四边形的面积是（ ）cm2。



相似考题

1.一个平行四边形和一个三角形等底等高。已知平行四边形的面积是30cm²，三角形的面积是多少？

2.在平行四边形ABCD中，∠DAB＝60°，AB＝15cm．已知⊙O的半径等于3cm，AB，AD分别与⊙O相切于点E，F，⊙O在平行四边形ABCD内沿AB方向滚动，与BC边相切时运动停止，试求⊙O滚过的路程．

3.如果一个四边形是轴对称图形，而且有两条互相垂直的对称轴，那么这个四边形一定是菱形吗？为什么？

4.用字母表示： （1）加法结合律：____________________________________________________； （2）乘法结合律：___________________________________________； （3）乘法对加法的分配律：_______________________________________； （4）一个长方形的长为b，宽是长的一半，它的周长是______；面积是______； （5）一个三角形的三边长都为c，它的周长是______； （6）一个平行四边形的一边长为a，该边上的高是其长的2/3 ，这个平行四边形的面积是______。

更多“如图，已知一个四边形中边AD长为3cm，边BC长7cm；∠DAB＝135°，∠ABC=∠ADC=90°那么这个四边形的面积是（ ）cm2。 ”相关问题

  • 第1题：

    （1）如果一个菱形绕对角线的交点旋转90°后，所得图形与原来的图形重合，那么这个菱形 是正方形吗？为什么？

    （2）如果一个四边形绕对角线的交点旋转90°后，所得图形与原来的图形重合，那么这个四边形是正方形吗？为什么？


    （1）是正方形。因为对角线相等的菱形是正方形

    （2）是正方形。不难证明对角线相等，四条边相等。


  • 第2题：

    平行四边形中，已知AB、BC及其夹角∠ B（∠ B是锐角），能求出平行四边形ABCD的面积S吗？如果能，写出用AB，BC及其夹角∠ B表示S的式子。


     

    S=BC×AB×sinB


  • 第3题：

    如图，四边形ABCD与四边形DEFG都是矩形，顶点F在BA的延长线上，边DG与AF交于点H，AD=4，DH=5，EF=6，求FG的长.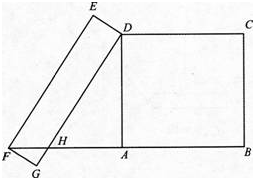


    答案：
    解析：
    解：∵四边形ABCD和四边形DEFG均为矩形，
    ∴∠DAF=∠DAB=90°，∠G=90°，DG=EF.
    ∵EF=6，DH=5，∴GH=DG-DH=EF-DH=6-5=1
    在Rt△ADH中，AD=4，DH=5，

  • 第4题：

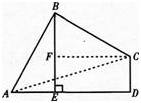
    如图，在四边形ABCD中，∠ABC=90°，CD⊥AD，AD2+CD2=2AB2.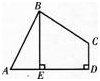

    (1)求证：AB=BC；
    (2)当BE⊥AD于E时，试证明：BE=AE+CD.


    答案：
    解析：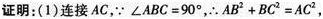



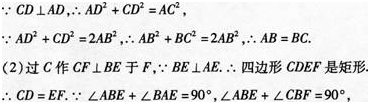
  • 第5题：

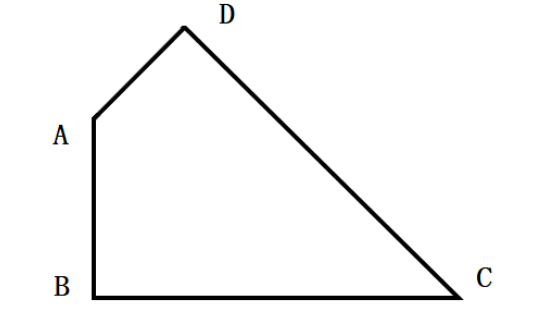
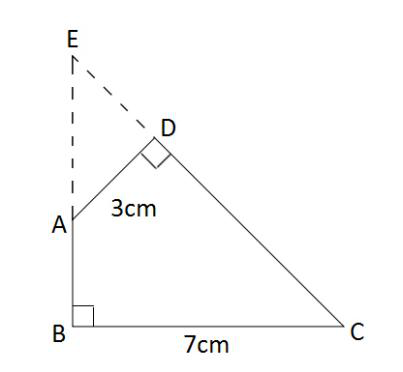
    如图，已知一个四边形中边AD长为3cm，边BC长7cm；∠DAB＝135°，∠ABC=∠ADC=90°那么这个四边形的面积是（ ）cm2。




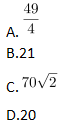    答案：D
    解析：
    第一步，本题考查几何问题，用割补平移法解题。
    第二步，作BA和CD的延长线交于E，如图所示，得到三角形EBC和ADE。容易知道所求四边形ABCD面积等于△EBC面积减去△ADE面积。由题意∠DAB＝135°，∠ABC＝∠ADC＝90°，可以求得∠DCB＝360°－135°－90°×2＝45°，且∠BEC＝∠EAD＝45°，所以△EBC和△ADE都是等腰直角三角形。
    第三步，因为AD长3cm，BC长7cm，则BE＝BC＝7cm，DE＝AD＝3cm，所以


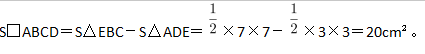
  • 第6题：

    如图，平行四边形ABCD，∠ADC的角平分线DE交BC于E,且AD=14，DC=9，则BE/EC的值为()。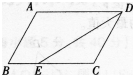

    A.1/3
    B.4/9
    C.5/9
    D.2/3

    答案：C
    解析：
    AD∥BC，则∠ADE=∠DEC，又∠ADE=∠CDE，所以△CDE为等腰三角形，EC=CD=9，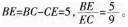

  • 第7题：

    如图所示，△ABC是直角形，四边形IBFD和四边形HFGE都是正方形，已知AI=1cm，IB＝4cm，问正方形HFGE的面积是多少（ ）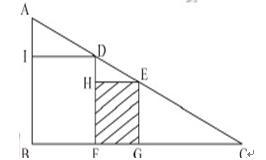



    答案：C
    解析：
    C。设正方形HFGE的边长为X，由三角形EHD相似于三角形DIA可知，EH/DH=DI/DA，即X/（X-4）=4/1，解得X=16/5，那么正方形面积为X的平方等于10.24。

  • 第8题：

    如图所示，ΔABC是直角三角形，四边形和四边形HFGE都是正方形，已知AI=1cm，IB=4cm，问正方形HFGE的面积是多少？（ ）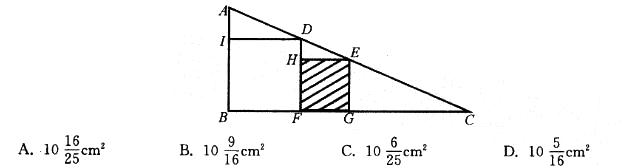


    答案：C
    解析：
    根据题意，AB = 5cm,ID=BF=4cm，我们利用比例关系“AI : ID = AB : BC”可得 BC=20cm,那么FC=BC-BF=16(cm)。我们假设EG=FG=xcm，那么GC=16-x，再利用比例关系"AB : BC=EG : GC”，得到5 : 20 = x : (16-x),解得x=3. 2，那么正方形HFGE 的面积为x2=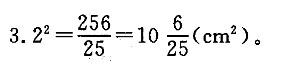

  • 第9题：

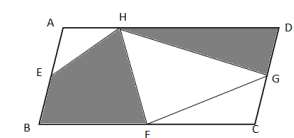
    如图，平行四边形ABCD的面积是54平方厘米，点E、F、G分别是平行四边形ABCD边上的中点，H为AD边上的任意一点，则阴影部分的面积为（ ）平方厘米。


    A. 27
    B. 28
    C. 32
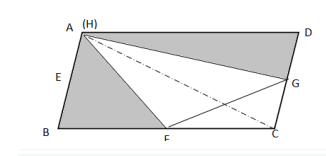
    D. 36

    答案：A
    解析：
    方法一：如图所示，由于H为AD边上的任意一点，假设H点与A点重叠，则左边阴影为三角形ABF，其面积为三角形ABC的一半；右边阴影为三角形ADG，其面积为三角形ACD的一半。因此题目所求为平行四边形ABCD面积的一半，平行四边形ABCD的面积是54平方厘米，则阴影部分面积为27平方厘米。因此，本题答案为A选项。



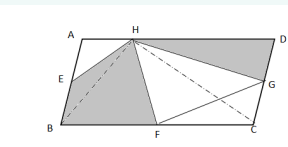
    方法二：如图所示，连接BH和CH，由于点E、F、G分别是平行四边形ABCD边上的中点，则三角形AEH和BEH相等，三角形BFH和CFH相等，三角形CGH和DGH相等，因此题目所求的阴影部分为平行四边形ABCD的一半。平行四边形ABCD的面积是54平方厘米，则阴影部分面积为27平方厘米。因此，本题答案为A选项。

  • 第10题：

    平行四边形的面积是（）

    • A、长a×宽b
    • B、宽b×高h
    • C、长a×宽b×高h
    • D、长a×高h

    正确答案:B

  • 第11题：

    两个同样的梯形，上底长23厘米，下底长27厘米，高20厘米。如果把这两个梯形拼成一个平行四边形，这个平行四边形的面积是（）平方厘米。

    • A、500
    • B、50
    • C、1000

    正确答案:C

  • 第12题：

    单选题
    两个同样的梯形，上底长23厘米，下底长27厘米，高20厘米。如果把这两个梯形拼成一个平行四边形，这个平行四边形的面积是()平方厘米。
    A

    500

    B

    50

    C

    1000


    正确答案： C
    解析： 暂无解析

  • 第13题：

    如果一个四边形是中心对称图形，那么这个四边形一定是平行四边形吗？为什么？


    是平行四边形

    由中心对称性可知，这个四边形相对的每个顶点分别是中心对称图形上的一对对应点，他们的连线被对称中心平分，即两条对角线相互平分，所以这个四边形一定是平行四边形！


  • 第14题：

    对边相等,对角相等的凸四边形,是平行四边形吧?

    方法①∠B小于90°；

    左上为A，左下为B，右下为C，右上为D；

    已知∠B=∠D；AB=CD;

    证明：过A作AN⊥BC于N；

          过C作CM⊥AD于M；

          连接AC

    ∵AN⊥BC；CM⊥AD

    ∴∠ANB=∠DMC=90°

    又∵∠B=∠D；AB=CD

    ∴△ANB=△DMC(AAS）

    ∴AN=CM;BN=DM

    又∵∠ANB=∠DMC=90°，AC=AC

    ∴△ACD=△AMD（HL）

    ∴AM=DN

    又∵BN=DM

    ∴BD=AC

    ∵BD=AC；AB=CD

    ∴凸四边形ABCD为平行四边型。

    方法②∠B大于90°

    左上为A，左下为B，右下为C，右上为D；

    已知∠B=∠D；AB=CD;

    证明：延长CD,过A作AN⊥BC于N；

          延长AB,过C作CM⊥AD于M；

          连接AC

    ∵AN⊥BC；CM⊥AD

    ∴∠ANB=∠DMC=90°

    又∵∠B=∠D；AB=CD

    ∴△ANB=△DMC(AAS）

    ∴AN=CM;BN=DM

    又∵∠ANB=∠DMC=90°，AC=AC

    ∴△ACD=△AMD（HL）

    ∴AM=DN

    又∵BN=DM

    ∴BD=AC

    ∵BD=AC；AB=CD

    ∴凸四边形ABCD为平行四边型。

    方法③∠B等于90°

    证明：∵∠B=∠D=90°；AB=CD；AC=AC

    ∴△ABC=△ADC（HL）

    ∴AB=CB

    ∵BD=AC；AB=CD

    ∴凸四边形ABCD为平行四边型。

    有错吗？若我的证明有错请明示，我知道有个反例，但它是凹四边形。


    是平行四边形

  • 第15题：

    在平行四边形ABCD中，∠DAB=60，AB=15cm，已知圆O的半径等于3cm，AB，AD分别与圆O相切于点E，F.圆0在平行四边形ABCD内沿AB方向滚动，与BC边相切时运动停止．试求圆O滚过的路程．


    答案：
    解析：

  • 第16题：

    如图，Rt△ABC中，∠ABC=90o,AB=28 cm，以AB为直径的半圆与AC相交，图中的阴影部分①的面积比⑦的面积少28.28 cm2，求BC的长(π取3．14)。


    答案：
    解析：

  • 第17题：

    如图，平面四边形ABCD中，AB=2，BC=4，CD=5，DA=3，
    (1)若∠B与∠D互补，求AC2的值；
    (2)求平面四边形ABCD面积的最大值。


    答案：
    解析：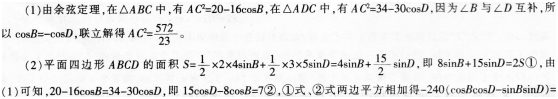

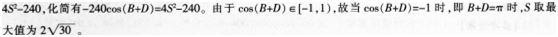
  • 第18题：

    如图，已知图中四边形两条边的长度和三个角的度数，四边形ABCD的面积是______cm2。


    答案：
    解析：
    24。解析：延长AD和BC交于点E，则得到两个等腰直角三角形△ABE和△DCE，四边形ABCD

  • 第19题：

    如图，已知一个四边形中边AD长为3cm，边BC长7cm；∠DAB＝135°，∠ABC=∠ADC=90°那么这个四边形的面积是（ ）。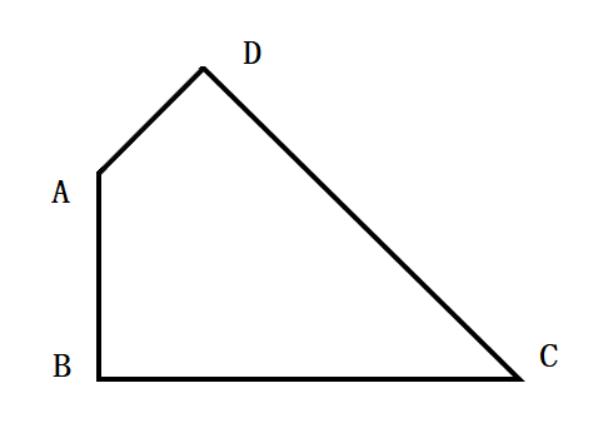


    A.49/4
    B.21
    C.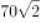
    D.20


    答案：D
    解析：

  • 第20题：

    如图7，在四边形ABCD中，AD∥BC，要使四边形ABCD为平行四边形，则应添加的条件是__________（添加一个条件即可）。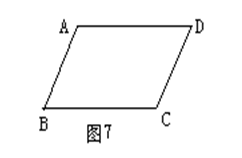


    答案：
    解析：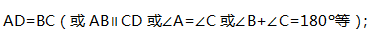

  • 第21题：

    如图，平行四边形ABCD，∠ADC的角平分线DE交BC于E，且AD=14，DC=9，




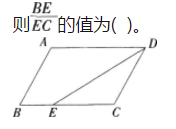
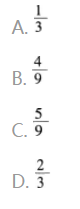    答案：C
    解析：

  • 第22题：

    日常生活中，我们随处可见四边形的物体，那么有两组对边平行的四边形，这样的四边形邻角（）


    正确答案:互补

  • 第23题：

    婆罗摩笈多给出的四边形面积公式在只针对（）成立。

    • A、折四边形
    • B、凹四边形
    • C、圆内接四边形
    • D、圆外切四边形

    正确答案:C

  • 第24题：

    单选题
    婆罗摩笈多给出的四边形面积公式在只针对（）成立。
    A

    折四边形

    B

    凹四边形

    C

    圆内接四边形

    D

    圆外切四边形


    正确答案： D
    解析： 暂无解析

相关内容