有两个班的小学生要到少年宫参加活动，但只有一辆车接送。第一班的学生坐车从学校出发的同时，第二班学生开始步行；车到途中某处，让第一班学生下车步行，车立刻返回接第二班学生上车并直接开往少年宫。学生步行速度为每小时4公里，载学生时车速每小时40公里，空车每小时50公里。那么，要使两班学生同时到达少年宫，第一班学生步行了全程的几分之几？（学生上下车时间不计）（ ）A. 1/7B. 1/6C. 3/4D. 2/5

题目

有两个班的小学生要到少年宫参加活动，但只有一辆车接送。第一班的学生坐车从学校出发的同时，第二班学生开始步行；车到途中某处，让第一班学生下车步行，车立刻返回接第二班学生上车并直接开往少年宫。学生步行速度为每小时4公里，载学生时车速每小时40公里，空车每小时50公里。那么，要使两班学生同时到达少年宫，第一班学生步行了全程的几分之几？（学生上下车时间不计）（ ）

A. 1/7

B. 1/6

C. 3/4

D. 2/5

相似考题

1.● 某学校有多个班，每个班有多名学生但只能有一个班长，那么班长与学生这两 个实体之间的关系是 （57） 。（57）A.1：1 B．1：n C．n：1 D．m：n

2.某班参加体育活动的学生有25 人，参加音乐活动的有26 人，参加美术活动的有24 人，同时参加体、音活动的有16 人，同时参加音、美活动的有15 入，同时参加美、体活动的有14 人，三个组织都参加的有5 人，这个班共有多少名学生参加活动？（ ）。 A.24 B.26 C.30 D.35

3.某班有56名学生，每人都参加了a、b、c、d、e五个兴趣班中的其中一个，已知有27人参加a兴趣班，参加b兴趣班的人数第二多，参加c、d兴趣班的人数相同，e兴趣班的参加人数最少，只有6人。问参加b兴趣班的学生有多少个？ A.7个 B.8个 C.9个 D.10个

4.某学校有多个班，每个班有多名学生但只能有一个班长，那么班长与学生这两个实体之间的关系是(57)。A．1:1B．1:nC．n:1D．m:n

更多“有两个班的小学生要到少年宫参加活动,但只有一辆车接送。第一班的学生坐车从学校出发的同时,第 ”相关问题

  • 第1题：

    某班参加体育活动的学生有25人，参加音乐活动的有26人，参加美术活动的有24人，同时参加体、音活动的有16人，同时参加音、美活动的有15人，同时参加美、体活动的有14人，三个组织都参加的有5人，这个班共有多少名学生参加活动?（　　）

    A.24
    B.26
    C.30
    D.35逛街

    答案：D
    解析：
    典型的三个集合的容斥问题，由三个集合的容斥原理可以得到，这个班参加活动的学生有25+26+24-16-15-14+5=35人。

  • 第2题：

    有两个班的小学生要到少年宫参加活动，但只有一辆车接送，第一班的学生坐车从学校出发的同时，第二班学生开始步行；车到途中某处，让第一班的学生下车步行，车立刻返回接第二班学生上车，并直接开往少年宫，学生步行速度为每小时4千米，载学生时车速每小时40千米，空车每小时50千米。问：要使两班学生同时到达少年宫，第一班学生步行了全程的几分之几？（学生上下车时间不计）（）


    答案：D
    解析：
    根据题意，两个班的同学都是一段路步行一段路乘车，而乘车的速度比步行快，中间又没有停留，因此要同时到达少年宫，两个班的同学步行的路程一定要一样长。

    如图所示，A是学校，B是少年宫，C是第一班学生下车的地点，D是第二班学生上车的地点。由题意得，AD=BC，学生步行的时间与车从A开到C再回到D的时间相等。设AD=BC=x，CD=y，则有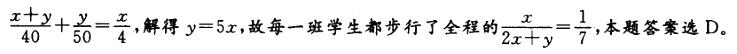

  • 第3题：

    刘老师调整教育策略，主动参加二班的一些集体活动，鼓励内向的同学发言，在学校举办的晚会上，他和二班学生一起唱歌。 请从学生观的角度评析刘老师的教育行为。(14分)


    答案：
    解析：
    刘老师的教学行为是值得赞扬的。刘老师的行为体现了素质教育的学生观。 全面发展的学生观，把学生看作发展的人，具有巨大的发展潜能。学生是独特的人，是完整的人。每个学生都是学习的主体，是具有 主观能动性的教育对象。刘老师做到了以上几点，调整教学策略，引导学生共同发展，体现了以学生为主体，把学生当成完整的人来 看待。刘老师认为学生是发展的，所以鼓励内向的学生发言，因材施教。晚会上拉近和同学之间的距离，把学生当作独立的个人对 待。

  • 第4题：

    有两个班的学生从南部校区到北部校区参加活动，但只有一辆车接送。第一班的学生坐车从学校出发的同时，第二个班的学生开始步行。车到途中某处，让第一个班的学生下车步行，车立刻返回接第二班学生上车并直接开往北部校区，学生步行速度为每小时4公里，汽车载学生时车速每小时40公里，空车每小时50公里。问：要使两班学生同时到达北部校区，第二班学生要步行全程的（ ）。


    答案：B
    解析：
    第一步，本题考查行程问题。
    第二步，两班同学同时出发，同时到达，又两班学生的步行速度相同，说明两班学生步行的距离和坐车的距离分别相同。设两个班学生步行的距离为x，坐车距离为y，则由题意有x/4=y/40+（y-x）/50，解得x∶y=1∶6，那么x占全程的1/（1+6）=1/7，即第二班的学生步行了全程的七分之一。
    因此，选择B选项。

  • 第5题：

    某班有80%的学生参加课外辅导班。其中参加英语辅导班的占全班总人数的40%，参加语文辅导班的占30%，参加数学辅导班的占50%。已知参加两个辅导班的学生人数与参加三个辅导班的学生人数的比例为3：1。问没参加课外辅导班的学生数与参加两个辅导班的学生人数的比例为（）。

    A.3：1
    B.2：1
    C.1：3
    D.1：2

    答案：C
    解析：
    设该班学生人数为100，参加两个辅导班的学生人数为a，参加三个辅导班的学生人数为b，则可知80=40+30+50-a+b，则a-b=40。又因为a：b=3：1，所以a=60。故没参加课外辅导班的学生数与参加两个辅导班的学生人数的比例为20：60=1：3。答案为C。

相关内容