某班参加体育活动的学生有25 人，参加音乐活动的有26 人，参加美术活动的有24 人，同时参加体、音活动的有16 人，同时参加音、美活动的有15 入，同时参加美、体活动的有14 人，三个组织都参加的有5 人，这个班共有多少名学生参加活动？（ ）。 A.24 B.26 C.30 D.35

题目
某班参加体育活动的学生有25 人，参加音乐活动的有26 人，参加美术活动的有24 人，同时参加体、音活动的有16 人，同时参加音、美活动的有15 入，同时参加美、体活动的有14 人，三个组织都参加的有5 人，这个班共有多少名学生参加活动？（ ）。

A.24
B.26
C.30
D.35
相似考题

1.五（1）班有25人，许多同学参加了课外小组。参加音乐组的有12人，参加美术组的有10人，两个组都没参加的有6人。既参加音乐组又参加美术组的有多少人？

2.某研究所共有三个科研小组，其中参加光谱研究小组的有20人，参加激光研究小组的有24人，参加色谱研究小组的有31人，同时参加光谱和激光两个小组的有5人，同时参加激光和色谱两个小组的有6人，同时参加光谱和色谱小组的有7人，三个小组都参加的有3人。问该研究所共有科研人员多少人?（ ） A．57 B．75 C．60 D．93

3.某校共有三个兴趣小组，分别为体育、书法和美术。已知参加这三个兴趣小组的学生分别是25人、24人、30人。同时参加体育、书法兴趣小组的有5人，同时参加体育、美术兴趣小组的有2人，同时参加书法、美术兴趣小组的有4人，有1人同时参加这三个兴趣小组，问：共有多少人参加兴趣小组?( )A.74B．72C．70D 69

4.50 名学生参加甲、乙两项体育活动，每人至少参加了一项，参加甲项的学生有30名，参加乙项的学生有25名，则仅参加了一项活动的学生人数为A．50 B．45 C．40 D．35

更多“某班参加体育活动的学生有25 人，参加音乐活动的有26 人，参加美术活动的有24 人，同时参加体、音活动的有16 人，同时参加音、美活动的有15 入，同时参加美、体活动的有14 人，三个组织都参加的有5 人，这个班共有多少名学生参加活动？（ ）。 ”相关问题

  • 第1题：

    某班有50名学生，参加语文竞赛的有28人，参加数学竞赛的有23人，参加英语竞赛的有20人，每人至多参加两科，那么参加两科的最多有多少人?（ ）

    A．28

    B．35

    C．39

    D．42


    正确答案：B

  • 第2题：

    某班有35个学生．每个学生至少参加英语小组、语文小组、数学小组中的一个课外活动小组。现已知参加英语小组的有17人，参加语文小组的有30人，参加数学小组的有13人。如果有5个学生三个小组全参加了，问有多少个学生只参加了一个小组（ ）

    A．15人

    B．16人

    C．17人

    D．18人


    正确答案：A
    设选两门课的人数为A，有(13+17+30)-A-2×5=35，得A=15。所以只报一门的人数为35-15-5=15。

  • 第3题：

    某班有40名学生，其中有15人参加数学小组，18人参加航模小组，有10人两个小组 都参加．那么有多少人两个小组都不参加?（ ） A．16 B．17 C．18 D．19


    正确答案：B
    依据题意，只参加数学小组的同学有15—10=5人，只参加航模小组的同学有18－10＝8人，两个小组都参加的同学有10人，所以有40一23＝17人两个小组都不参加。故选B。

  • 第4题：

    某班有50名学生，参加语文竞赛的有28人，参加数学竞赛的有23人，参加英语竞赛的有20人，每人至多参加两科，那么参加两科的最多有多少人？（ ）

    A. 28
    B. 35
    C. 39
    D. 42

    答案：B
    解析：
    画出图示，因为“每人最多参加两科”，所以没有人参加三科竞赛。由图可知：

  • 第5题：

    某班56名学生参加了奥数或作文课外兴趣小组的活动，其中参加奥数的有32人，参加作文的有35人，问两种活动都参加的有多少人?()

    A. 3
    B. 11
    C. 21
    D. 24

    答案：B
    解析：
    两种活动都参加得人有32+35-56=11人。故答案为B。

  • 第6题：

    某班有60人，参加物理竞赛的有30人，参加数学竞赛的有32人，两科都没有参加的有20人。同时参加物理、数学两科竞赛的有多少人：

    A28人
    B26人
    C24人
    D22人


    答案：D
    解析：

  • 第7题：

    某校共有三个兴趣小组，分别为体育、书法和美术。巳知参加这三个兴趣小组的学生分别 是25人、24人、30人。同时参加体育、书法兴趣小组的有5人，同时参加体育、美术兴趣 小组的有2人，同时参加书法、美术兴趣小组的有4人，有1人同时参加这三个兴趣小组， 共有（ ）人参加兴趣小组。
    A. 74 B. 72 C. 70 D. 69


    答案：D
    解析：
    根据文氏图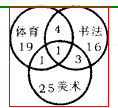：可得三个兴趣小组的总人数为25 + 24 + 30—(5 + 2 + 4) + 1==69(人）。所以答案选D。

  • 第8题：

    某班有36名同学参加数学、物理、化学课外研究小组,每名同学至多参加两个小组,已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有（ ）

    A.6人
    B.7人
    C.8人
    D.9人
    E.10人

    答案：C
    解析：
    由条件知,每名同学至多参加两个小组,故不可能出现一名同学同时参加数学、物理、化学课外研究小组,设同时参加数学和化学小组的有x人,根据容斥原理有26+15+13-（6+4+x）=36,解得x=8.故同时参加数学和化学小组的有8人,应选C.

  • 第9题：

    88名学生参加运动会，参加游泳比赛的有23人，参加田径比赛的有33人，参加球类比赛的有54人，既参加游泳比赛又参加田径比赛的有5人，既参加田径比赛又参加球类比赛的有16人。已知每名学生最多可参加两项比赛，问只参加田径比赛的有多少人（）

    • A、20
    • B、17
    • C、15
    • D、12

    正确答案:D

  • 第10题：

    共有110人参加A、B、C三科考试，每人至少参加一科。已知参加A考试的有52人.只参加A考试的有16人；参加8考试的有63人，只参加B考试的有21人；参加C考试的有61人，只参加C考试的有15人。那么三科考试都参加的有多少人？（）

    • A、8人
    • B、14人
    • C、58人
    • D、66人

    正确答案:A

  • 第11题：

    单选题
    共有110人参加A、B、C三科考试，每人至少参加一科。已知参加A考试的有52人.只参加A考试的有16人；参加8考试的有63人，只参加B考试的有21人；参加C考试的有61人，只参加C考试的有15人。那么三科考试都参加的有多少人？（）
    A

    8人

    B

    14人

    C

    58人

    D

    66人


    正确答案： C
    解析： 设三科都参加的是x人，列方程（52-16-x+63-21-x+61-15-x）÷2+x+16+21+15=110，x=8。

  • 第12题：

    单选题
    某班有60人，参加物理竞赛的有30人，参加数学竞赛的有32人，两者都没有参加的有20人。同时参加物理、数学两科竞赛的有多少人（  ）
    A

    28

    B

    26

    C

    24

    D

    22


    正确答案： A
    解析：

  • 第13题：

    某班有50名学生，参加英语竞赛的有28人，参加数学竞赛的有20人，参加物理竞赛的有23人，每人最多参加两科，那么只参加两科的最多有多少人?

    A．23

    B．35

    C．28

    D．21


    正确答案：B
    94．【答案】B。解析：参加竞赛的有28+20+23=71人次，要使参赛的人尽可能地参加两科，71÷2=35??l，所以至多有35人参加两科。

  • 第14题：

    某年级的课外小组分为美术、音乐、手工三个小组，参加美术小组有20人，参加音乐小组有24人，参加手工小组有31人，同时参加美术和音乐两个小组有5人，同时参加音乐和手工两个小组有6人，同时参加美术和手工两个小组的有7人，三个小组都参加的有3人，这个年级参加课外小组的同学共有多少人?（ ） A．75人 B．57人 C．63人 D． 60人


    正确答案：D
    如图所示，由容斥原理可知，这个年级参加课外小组的有20+24+31－(5+6+7)+3＝60人。故选D。

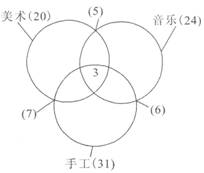
  • 第15题：

    某班有36名同学参加数学、物理、化学课外探究小组，每名同学至多参加两个小组，已知参加数学、物理、化学小组的人数分别为26，15，13，同时参加数学和物理小组的有6人，同时参加物理和化学小组的有4人，则同时参加数学和化学小组的有 人。


    正确答案：
    答案：8

  • 第16题：

    工厂组织工人参加技能培训，参加车工培训的有17人，参加钳工培训的有16人，参加铸工培训的有14人，参加两项及以上培训的人占参加培训总人数的2/3，三项培训都参加的有2人，问总共有多少人参加了培训？

    A. 24
    B. 27
    C. 30
    D. 33

    答案：B
    解析：

  • 第17题：

    某班参加学科竞赛人数40人，其中参加数学竞赛的有22人，参加物理竞赛的有27人，参加化学竞赛的有25人，只参加两科竞赛的有24人，参加三科竞赛的有多少人？

    A.2
    B.3
    C.5
    D.7

    答案：C
    解析：
    第一步，本题考查容斥问题，属于三集合容斥类，用公式法解题。
    第二步，设参加三科竞赛的有x人，根据三集合非标准型容斥原理公式可列方程：40－0＝22＋27＋25－24－2x，解得x＝5。

  • 第18题：

    某班参加体育活动的学生有25人，参加音乐活动的有26人，参加美术活动的有24人，同时参加体、音活动的有16人，同时参加音、美活动的有15人，同时参加美、体活动的有14人，三个组织都参加的有5人，这个班共有多少名学生参加活动?（　　）

    A.24
    B.26
    C.30
    D.35逛街

    答案：D
    解析：
    典型的三个集合的容斥问题，由三个集合的容斥原理可以得到，这个班参加活动的学生有25+26+24-16-15-14+5=35人。

  • 第19题：

    为丰富职工业余文化生活，某单位组织了合唱、象棋、羽毛球三项活动。在该单位的所有职工中，参加合唱活动有189人，参加象棋活动有152人，参加羽毛球活动有135人，参加两种活动的有130人，参加三种活动的有69人，不参加任何一种活动的有44人。该单位的职工人数为：

    A233
    B252
    C321
    D520


    答案：B
    解析：
    题目为三集合整体重复型容斥原理问题。根据三集合整体重复型容斥原理公式可以得出，该单位的职工人数（可根据计算尾数快速求解）。

    故正确答案为B。

  • 第20题：

    为了提升员工的专业技能，某公司开展了A、B、C三种技能培训活动，共有60人参加。其中，只参加A活动的有6人，只参加了B活动的有8人，只参加了C活动的有15人，同时参加A、B两种活动的有20人，同时参加B、C活动的有9人，同时参加A、C活动的有16人，则三种活动都参加的有多少人？（）

    • A、7
    • B、9
    • C、10
    • D、11

    正确答案:A

  • 第21题：

    某班有60人，参加物理竞赛的有30人，参加数学竞赛的有32人，两科都没有参加的有20人。同时参加物理、数学两科竞赛的有多少人？

    • A、28人 
    • B、26人 
    • C、24人 
    • D、22人

    正确答案:D

  • 第22题：

    有100人参加运动会的三个项目，每人至少参加一项，其中未参加跳远的有50人，未参加跳高的有60人，未参加赛跑的有70人，问至少有多少人参加了不只一项活动？（）

    • A、7
    • B、10
    • C、15
    • D、20

    正确答案:B

  • 第23题：

    单选题
    某班有学生50人，其中参加篮球队的有38人，参加足球队的有34人，参加排球队的有32人，篮球、足球都参加的有28人，足球、排球都参加的有24人，篮球、排球都参加的有26人，三项都参加的有20人，则只参加一项的人比三项都没参加的人多（）个。
    A

    2

    B

    3

    C

    4

    D

    5


    正确答案： B
    解析： 三集合容斥问题，用画图法。

相关内容