在自然数1至50中，将所有不能被3除尽的数相加，所得的和是：A、865 B、866 C、867 D、868

题目

在自然数1至50中，将所有不能被3除尽的数相加，所得的和是：

A、865 B、866 C、867 D、868

相似考题

1.1至100中所有不能被9整除的自然数的和是( )。A． 217B．594C．5050D．4456

2.1~100各数所有不能被整除的自然数的和是( )A.594 B.3854 C.4456 D.5050

3.1～100各数中所有不能被9整除的自然数的和是()。A. 217 B. 594 C. 5050 D. 4456

4.在自然数1至50中，将所有不能被3除尽的数相加，所得的和是( )。A．865B．866C．867D．868

更多“在自然数1至50中,将所有不能被3除尽的数相加,所得的和是: A、865 B、866 C、867 D、868 ”相关问题

  • 第1题：

    在1至100的自然数中，不能被2整除且不能被3整除且不能被5整除的数共有多少个?（ ） A．23个 B．26个 C．27个 D．74个


    正确答案：B

    1至100的自然数中，能被2整除的数有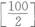=50个，能被3整除的数有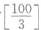=33个，能被5整除的数有=20个，能被2整除且能被3整除的数有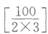＝16个，能被5整除且能被3整除的数有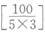＝6个，能被2整除且能被5整除的数有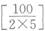＝10个，能被2整除且能被3整除且能被5整除的数有=3个，故由容斥原理，不能被2整除且不能被3整除且不能被5整除的数共有100－[50+33+20－(16+6+10)+3]=26个。故选B。

  • 第2题：

    在自然数1至50中，将所有不能被3除尽的数相加，所得的和是（ )。
    A. 865 B. 866 C. 867 D. 868


    答案：C
    解析：
    1—50所有数字的和为（l + 50)X50/2= 1275,1—50能被3整除的数字 和为（3 + 48) X 16/2 = 408，因此将所有不能被3除尽的数相加，和为1275 — 408 = 867。

  • 第3题：

    在自然数1至50中，将所有不能被3除尽的数相加,所得的和是（ ）。
    a. 865 b. 866c. 867 d. 868


    答案：C
    解析：
    1—50所有数字的和为（1 + 50) X50/2= 1275,1—50能被3整除的数字 和为（3 + 48)X16/2 = 408，因此将所有不能被3除尽的数相加，和为1275 — 408 = 867。

  • 第4题：

    1至1000中所有不能被5，6，8整除的自然数有多少个？（）

    A. 491
    B. 107
    C. 400
    D. 600

    答案：D
    解析：
    只要求出1-1000内5的倍数、6的倍数或8的倍数或5X6，5X8，24，120的倍数， 再根据容斥原理就可求得。
    5的倍数有5、10…1000共200个；
    6的倍数有6、12…996共166个；
    8的倍数有8、16…共125个；
    24的倍数有24、48...984共41个；
    30的倍数有30、60…990共33个；
    40的倍数有40、80…1000共25个；
    120的倍数有120、240…960共8个。
    根据容斥原理可知，5或6或8的倍数有：
    (200 + 166 + 125)-(33 + 25+41)+8 = 400（个）。
    不能被5或6或8中任一个整除的有1000-400 = 600（个）。
    故本题选D。

  • 第5题：

    在自然数1至50中，将所有不能被3除尽的数相加，所得的和是：


    A. 865
    B. 866
    C. 867
    D. 868

    答案：C
    解析：
    解题指导： 1+2+3+4+……+50-（3+6+9+……+48）=50*51/2-3*16*17/2=1275-408=867。故答案为C。

相关内容