最优二叉树(哈夫曼树)、最优查找树均为平均查找路径长度Σwl最小的树，其中对于最优二叉树，n表示(42)；对于最优查找树，n表示(43)；构造这两种树均(44)。A．结点数B．叶结点数C．非叶结点数D．度为二的结点数

题目

最优二叉树(哈夫曼树)、最优查找树均为平均查找路径长度Σwl最小的树，其中对于最优二叉树，n表示(42)；对于最优查找树，n表示(43)；构造这两种树均(44)。

A．结点数

B．叶结点数

C．非叶结点数

D．度为二的结点数

相似考题

1.哈夫曼树又称为最优二叉树。()此题为判断题(对，错)。

2.● 若用n个权值构造一棵最优二叉树 （哈夫曼树）， 则该二叉树的结点总数为 （59） 。

3.若用n个权值构造一棵最优二叉树(哈夫曼树)，则该二叉树的结点总数为(59)。A．2nB．2n-1C．2n+lD．2n+2

4.关于哈夫曼树、最优二叉树、哈夫曼算法，有以下说法：①最优二叉树的形态不唯一，但是其WPL值是唯一确定的。②哈夫曼树一定是最优二叉树，但最优二叉树不一定由哈夫曼算法来构造。则______。A．①正确②错误B．①错误②正确C．都对D．都错

更多“最优二叉树(哈夫曼树)、最优查找树均为平均查找路径长度Σwl最小的树,其中对于最优二叉树,n表示(42 ”相关问题

  • 第1题：

    最优二叉树(哈夫曼树)、最优查找树均为平均查找路径长度∑wl最小的树，其中对于最优二叉树，n表示(31)；对于最优查找树，n表示(32)；构造这两种树均(33)。

    A．节点数

    B．叶节点数

    C．非叶节点数

    D．度为2的节点数


    正确答案：B
    解析：(31)～(33)(31)假设有n个权值{w1,w2,…，wn)，是构造一棵有n个叶子节点的二又树，每个叶子节点带权wi，则其中带权路径长度WPL=∑wili最小的二又树称做最优二又树或哈夫曼树。所以最优二叉树中n表示叶节点。(32)如果只考虑查找成功的情况，则使查找性能达到最佳的判定树是其带权内路径长度之和值PH=∑wili，取最小值的二叉树为最优查找树。其中n为二叉树上节点的个数(即有序表的长度)；li为第i个节点在二叉树上的层次数；节点的权wi=cpi(i=1～n)，其中pi为节点的查找概率，c为某个常量。因此最优查找树中n表示所有节点数。(33)构造哈夫曼树和最优查找树均需对n个关键字进行动态插入。

  • 第2题：

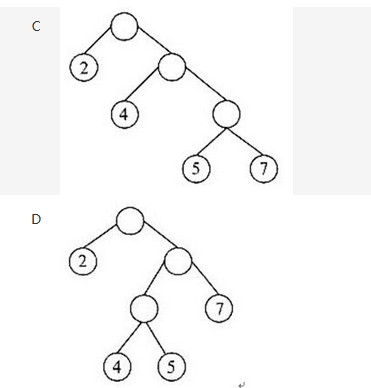
    最优二叉树(或哈夫曼树)是指权值为w1，w2，…，wn的n个叶结点的二叉树中带权路径长度最小的二叉树。( )是哈夫曼树(叶结点中的数字为其权值)。



    答案：A
    解析：
    本题考查数据结构基础知识。
    哈夫曼树又称为最优二叉树，是一类带权路径长度最短的树。
    树的带权路径长度(WPL)为树中所有叶子结点的带权路径长度之和，记为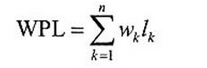

    其中n为带权叶子结点数目，wk为叶子结点的权值，lk为根到叶子结点的路径长度。
    选项A所示二叉树的WPL=(2+4)*3+5*2+7*1=35
    选项B所示二叉树的WPL=(2+4+5+7)*2=36
    选项C所示二叉树的WPL=(5+7)*3+4*2+2*1=46
    选项D所示二叉树的WPL=(4+5)*3+7*2+2*1=43

  • 第3题：

    2、哈夫曼树是树的带权路径长度最小的二叉树


    A

  • 第4题：

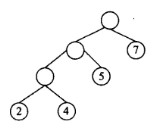
    最优二叉树(或哈夫曼树)是指权值为 W1， W2，。。。，Wn 的 n 个叶结点的二叉树中带权路径长度最小的二叉树。（ ）是哈夫曼树(叶结点中的数字为其权值)。

    A.

    B.

    C.

    D.


    正确答案：A

  • 第5题：

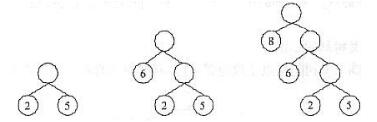
    （ ）是由权值集合{8，5，6，2}构造的哈夫曼树（最优二叉树）。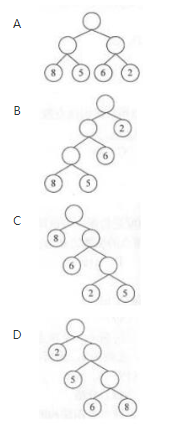


    答案：C
    解析：
    本题考查二叉树应用知识。构造最优二叉树的哈夫曼算法如下：①根据给定的n个权值{W1，W2，...，Wn}，构成n棵二叉树的集合F={T1，T2，...，Tn}，其中每棵二叉树Ti中只有一个带权为Wi的根结点，其左右子树均空。②在F中选取两棵权值最小的二叉树作为左、右子树构造一棵新的二叉树，置新构造二叉树的根结点的权值为其左、右子树根结点的权值之和。③从F中删除这两棵树，同时将新得到的二叉树加入到F中。重复②、③，直到F中只含一棵树时为止。这棵树便是最优二叉树(哈夫曼树)。根据题中给出的权值集合，构造哈夫曼树的过程如下图所示。

相关内容