若用n个权值构造一棵最优二叉树(哈夫曼树)，则该二叉树的结点总数为(59)。A．2nB．2n-1C．2n+lD．2n+2

题目

若用n个权值构造一棵最优二叉树(哈夫曼树)，则该二叉树的结点总数为(59)。

A．2n

B．2n-1

C．2n+l

D．2n+2

相似考题

1.以下说法错误的是 ( )A.一般在哈夫曼树中，权值越大的叶子离根结点越近B.哈夫曼树中没有度数为1的分支结点C.若初始森林中共有n裸二叉树，最终求得的哈夫曼树共有2n-1个结点D.若初始森林中共有n裸二叉树，进行2n-1次合并后才能剩下一棵最终的哈夫曼树

2.(1)以2,3,4,7,8,9作为叶结点的权，构造一棵哈夫曼树(要求每个结点的左子树根结点的权小于等于右子树根结点的权)，给出相应权重值叶结点的哈夫曼编码。(2)一棵哈夫曼树有n个叶结点，它一共有多少个结点?简述理由。

3.最优二叉树(哈夫曼树)、最优查找树均为平均查找路径长度Σwl最小的树，其中对于最优二叉树，n表示(42)；对于最优查找树，n表示(43)；构造这两种树均(44)。A．结点数B．叶结点数C．非叶结点数D．度为二的结点数

4.若用n个权值构造一颗最优二叉树(哈夫曼树)，则该二叉树的结点总数为()A.2nB.2n-1C.2n+1D.2n+2

更多“若用n个权值构造一棵最优二叉树(哈夫曼树)，则该二叉树的结点总数为(59)。A．2nB．2n-1C．2n+lD．2n+2”相关问题

  • 第1题：

    关于哈夫曼树、最优二叉树、哈夫曼算法，有以下说法：

    ①最优二叉树的形态不唯一，但是其WPL值是唯一确定的。

    ②哈夫曼树一定是最优二叉树，但最优二叉树不一定由哈夫曼算法来构造。

    则______。

    A．①正确②错误

    B．①错误②正确

    C．都对

    D．都错


    正确答案：C
    解析：假设有n个权值{w1，w2，…，wn)，构造一棵有n个叶子结点的二叉树，则称带权路径长度WPL最小的二叉树为最优二叉树，亦称哈夫曼树。值得注意的是，最优二叉树的形态不唯一，但是其WPL值是唯一确定的。这好比一个班里，张三、李四和王五体型各异但身高一样，而且是最高的，显然最高的身高值只有一个。用哈夫曼算法构造出来的哈夫曼树一定是最优二叉树，定性地说，在哈夫曼算法中，每次构造新树时都是将权值最小的树尽量放在离根最远的地方，而将权值大的尽量放在离根近的地方，从而使得WPL最小。因此，哈夫曼树一定是最优二叉树。值得特别注意的是，哈夫曼算法可以确保构造出来的树是最优二叉树，但是最优二叉树并不一定非得用哈夫曼算法来构造。例如，给定权值{2，3，4，7，8，9}，可以构造出两棵最优二叉树T1、T2，如图3-72所示。显然它们的WPL都是80，所以T1、T2都是是最优二叉树。T1是用哈夫曼算法构造出来的，但T2却不是用哈夫曼算法构造出来的，而是用上文中提及的构造哈夫曼树最容易犯的错误想法构造出来的一棵树。从上面的例子可以看出，哈夫曼算法只是构造最优二叉树的“充分条件”，而不是“必要条件”。至于为什么将哈夫曼树称为最优二叉树，原因可能是由于哈夫曼最早给出了带有一般规律的构造最优二叉树的哈夫曼算法，为了纪念他，就用哈夫曼树来称呼所有的最优二叉树。

  • 第2题：

    以下关于哈夫曼树的叙述,正确的是(60)。A.哈夫曼树一定是满二叉树,其每层结点数都达到最大值SX

    以下关于哈夫曼树的叙述，正确的是（60）。

    A.哈夫曼树一定是满二叉树，其每层结点数都达到最大值

    B.哈夫曼树一定是平衡二叉树，其每个结点左右子树的高度差为-1、0或1

    C.哈夫曼树中左孩子结点的权值小于父节点、右孩子节点的权值大于父节点

    D.哈夫曼树中叶子节点的权值越小则距离树根越远、叶子结点的权值越大则距离树根越近


    正确答案：D
    给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。所以D选项的说法正确。

  • 第3题：

    下列关于哈夫曼树的叙述错误的是

    A．一棵哈夫曼树是带权路径长度最短的二叉树

    B．一棵哈夫曼树中叶结点的个数比非叶结点的个数大1

    C．一棵哈夫曼树结点的度要么是0，要么是2

    D．哈夫曼树的根结点的权值等于各个叶子结点的权值之和


    正确答案：C
    解析：哈夫曼树中结点的度可以是0，1，2。

  • 第4题：

    最优二叉树(或哈夫曼树)是指权值为 W1， W2，。。。，Wn 的 n 个叶结点的二叉树中带权路径长度最小的二叉树。（ ）是哈夫曼树(叶结点中的数字为其权值)。

    A.

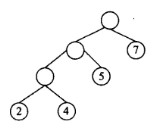
    B.

    C.

    D.


    正确答案：A

  • 第5题：

    ● 下面关于哈夫曼树的叙述中，正确的是 （58） 。

    （58）

    A. 哈夫曼树一定是完全二叉树

    B. 哈夫曼树一定是平衡二叉树

    C. 哈夫曼树中权值最小的两个结点互为兄弟结点

    D. 哈夫曼树中左孩子结点小于父结点、右孩子结点大于父结点


    正确答案：C

  • 第6题：

    设有13个值，用它们组成一棵哈夫曼树，则该哈夫曼树共有()个结点。

    A.13
    B.12
    C.26
    D.25

    答案：D
    解析：
    哈夫曼树的特点：具有n个叶子结点的哈夫曼树共有2×n-1个结点。

  • 第7题：

    （ ）是由权值集合{8，5，6，2}构造的哈夫曼树（最优二叉树）。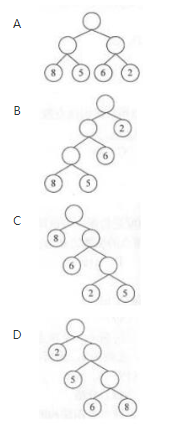


    答案：C
    解析：
    本题考查二叉树应用知识。构造最优二叉树的哈夫曼算法如下：①根据给定的n个权值{W1，W2，...，Wn}，构成n棵二叉树的集合F={T1，T2，...，Tn}，其中每棵二叉树Ti中只有一个带权为Wi的根结点，其左右子树均空。②在F中选取两棵权值最小的二叉树作为左、右子树构造一棵新的二叉树，置新构造二叉树的根结点的权值为其左、右子树根结点的权值之和。③从F中删除这两棵树，同时将新得到的二叉树加入到F中。重复②、③，直到F中只含一棵树时为止。这棵树便是最优二叉树(哈夫曼树)。根据题中给出的权值集合，构造哈夫曼树的过程如下图所示。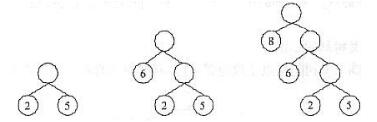

  • 第8题：

    以2，3，4，7，8，9作为叶结点的权，构造一棵哈夫曼树，给出相应权重值叶结点的哈夫曼编码。

    2  0000
    3  0001
    4  001
    7  10
    8  11
    9  01
    略

  • 第9题：

    n（n≥2）个权值均不相同的字符构成哈夫曼树，关于该树的叙述中，错误的是（）。

    • A、该树一定是一棵完全二叉树
    • B、树中一定没有度为1的结点
    • C、树中两个权值最小的结点一定是兄弟结点
    • D、树中任一非叶结点的权值一定不小于下一层任一结点的权值

    正确答案:A

  • 第10题：

    一棵有n个叶结点的哈夫曼树，则该树共有（）个结点。


    正确答案:2n-1

  • 第11题：

    填空题
    哈夫曼树又称为（），它是n个带权叶子结点构成的所有二叉树中带权路径长度WPL（）。

    正确答案： 最优二叉树,最小的二叉树
    解析： 暂无解析

  • 第12题：

    填空题
    一棵有n个叶结点的哈夫曼树，则该树共有（）个结点。

    正确答案： 2n-1
    解析： 暂无解析

  • 第13题：

    ● 若用n个权值构造一棵最优二叉树 （哈夫曼树）， 则该二叉树的结点总数为 （59） 。


    正确答案：B

  • 第14题：

    下列关于哈夫曼树的叙述错误的是

    A．一棵哈夫曼树是带权路径长度最短的二叉树

    B．一棵哈夫曼树中叶节点的个数比非叶节点的个数大1

    C．一棵哈夫曼树节点的度要么是0，要么是2

    D．哈夫曼树的根节点的权值等于各个叶节点的权值之和


    正确答案：C
    解析：哈夫曼树中节点的度可以是0，1，2。

  • 第15题：

    由权值为5，9，2，6的4个叶子构造一棵哈夫曼树，该树的带权路径长度为(59)。

    A．21

    B．22

    C．42

    D．44


    正确答案：C
    解析：根据哈夫曼算法，由权值为5，9，2，6的 4个叶子构造一棵哈夫曼树，如图4-9所示。

    图4-9哈夫曼树的权W(T)=(2+5)×3+6×2+9×1=42。

  • 第16题：

    下列有关树的叙述中不正确的是【】

    A．二叉树中每个结点有两个子结点，而树无此限制，因此二叉树是树的特殊情况

    B．当K≥1时高度为K的二叉树至多有2k-l个结点

    C．将一棵树转换成二叉树后，根结点没有左子树

    D．哈夫曼树是带权路径最短的树，路径上权值较大的结点离根较近


    正确答案：ABC
    [解析]二叉树是树形结构的一个重要类型,二叉树不是树，也不是树的特殊情况．当K1时高度为K的二叉树至多有2k-1个结点，而不是2k-1个结点．由于树的根结点没有兄弟，将一棵树转换成二又树后根结点没有右子树．

  • 第17题：

    最优二叉树(或哈夫曼树)是指权值为w1，w2，…，wn的n个叶结点的二叉树中带权路径长度最小的二叉树。( )是哈夫曼树(叶结点中的数字为其权值)。



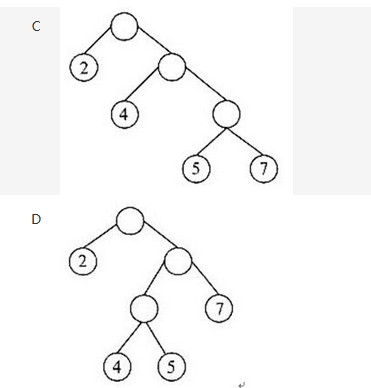    答案：A
    解析：
    本题考查数据结构基础知识。
    哈夫曼树又称为最优二叉树，是一类带权路径长度最短的树。
    树的带权路径长度(WPL)为树中所有叶子结点的带权路径长度之和，记为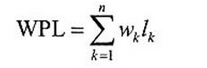

    其中n为带权叶子结点数目，wk为叶子结点的权值，lk为根到叶子结点的路径长度。
    选项A所示二叉树的WPL=(2+4)*3+5*2+7*1=35
    选项B所示二叉树的WPL=(2+4+5+7)*2=36
    选项C所示二叉树的WPL=(5+7)*3+4*2+2*1=46
    选项D所示二叉树的WPL=(4+5)*3+7*2+2*1=43

  • 第18题：

    下面关于哈夫曼树的叙述中，正确的是（ ）。

    A.哈夫曼树一定是完全二叉树
    B.哈夫曼树一定是平衡二叉树
    C.哈夫曼树中权值最小的两个结点互为兄弟结点
    D.哈夫曼树中左孩子结点小于父结点、右孩子结点大于父结点

    答案：C
    解析：
    哈夫曼树是一种特殊的二叉树，但它不是完全二叉树，也不是平衡二叉树，给出n个权值{w1，w2，…，wn}构造一棵具有n个叶子结点的哈夫曼树的方法如下：
    第一步，构造n个只有根结点的二叉树集合F={T1，T2，…，Tn}，其中每棵二叉树Ti的根结点带权为Wi（1≤k≤n）
    第二步，在集合F中选取两棵根结点的权值最小的二叉树作为左右子树，构造一棵新的二叉树，令新二叉树根结点的权值为其左、右子树上根结点的权值之和
    第三步，在F中删除这两棵二叉树，同时将新得到的二叉树加入到F中
    第四步，重复第二步和第三步，直到F只含有一棵二叉树为止，这棵二叉树便是哈夫曼树
    综上所述，我们可以知道哈夫曼树中权值最小的两个结点互为兄弟结点

  • 第19题：

    哈夫曼树又称为（），它是n个带权叶子结点构成的所有二叉树中带权路径长度WPL（）。
    最优二叉树；最小的二叉树
    略

  • 第20题：

    （）又是一棵满二叉树。

    • A、二叉排序树
    • B、深度为5有31个结点的二叉树
    • C、有15个结点的完全二叉树
    • D、哈夫曼（Huffman）树（没有度为1的结点）

    正确答案:C

  • 第21题：

    一棵有16个叶结点的哈夫曼树，则该树共有（）个结点。


    正确答案:31

  • 第22题：

    单选题
    设给定权值总数有n个，其哈夫曼二叉树的结点总数为（  ）。
    A

    不确定

    B

    2n

    C

    2n+1

    D

    2n-l


    正确答案： D
    解析：

  • 第23题：

    单选题
    （）又是一棵满二叉树。
    A

    二叉排序树

    B

    深度为5有31个结点的二叉树

    C

    有15个结点的完全二叉树

    D

    哈夫曼（Huffman）树（没有度为1的结点）


    正确答案： D
    解析： 暂无解析

相关内容