若用n个权值构造一颗最优二叉树(哈夫曼树),则该二叉树的结点总数为()A.2nB.2n-1C.2n+1D.2n+2
题目
若用n个权值构造一颗最优二叉树(哈夫曼树),则该二叉树的结点总数为()
A.2n
B.2n-1
C.2n+1
D.2n+2
相似考题
参考答案和解析
正确答案:B
更多“若用n个权值构造一颗最优二叉树(哈夫曼树),则该二叉树的结点总数为()A.2nB.2n-1C.2n+1D.2n+2 ”相关问题
-
第1题:
最优二叉树(或哈夫曼树)是指权值为w1,w2,…,wn的n个叶结点的二叉树中带权路径长度最小的二叉树。( )是哈夫曼树(叶结点中的数字为其权值)。
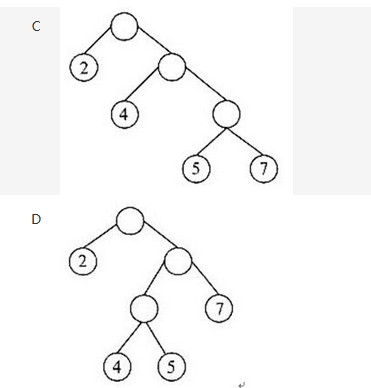 答案:A解析:本题考查数据结构基础知识。
答案:A解析:本题考查数据结构基础知识。
哈夫曼树又称为最优二叉树,是一类带权路径长度最短的树。
树的带权路径长度(WPL)为树中所有叶子结点的带权路径长度之和,记为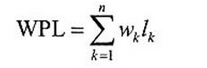
其中n为带权叶子结点数目,wk为叶子结点的权值,lk为根到叶子结点的路径长度。
选项A所示二叉树的WPL=(2+4)*3+5*2+7*1=35
选项B所示二叉树的WPL=(2+4+5+7)*2=36
选项C所示二叉树的WPL=(5+7)*3+4*2+2*1=46
选项D所示二叉树的WPL=(4+5)*3+7*2+2*1=43 -
第2题:
用13个权值构造哈夫曼树,则该哈夫曼树共有 个结点。
A.13
B.12
C.26
D.25
D 解析:具有n个叶子结点的哈夫曼树共有2*n-1个结点。 -
第3题:
38、用13个权值构造哈夫曼树,则该哈夫曼树共有 个结点。
A.13
B.12
C.26
D.25
25 -
第4题:
( )是由权值集合{8,5,6,2}构造的哈夫曼树(最优二叉树)。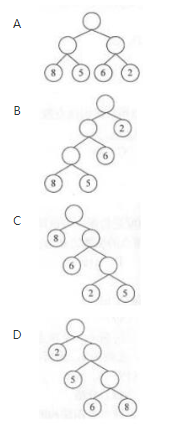 答案:C解析:本题考查二叉树应用知识。构造最优二叉树的哈夫曼算法如下:①根据给定的n个权值{W1,W2,...,Wn},构成n棵二叉树的集合F={T1,T2,...,Tn},其中每棵二叉树Ti中只有一个带权为Wi的根结点,其左右子树均空。②在F中选取两棵权值最小的二叉树作为左、右子树构造一棵新的二叉树,置新构造二叉树的根结点的权值为其左、右子树根结点的权值之和。③从F中删除这两棵树,同时将新得到的二叉树加入到F中。重复②、③,直到F中只含一棵树时为止。这棵树便是最优二叉树(哈夫曼树)。根据题中给出的权值集合,构造哈夫曼树的过程如下图所示。
答案:C解析:本题考查二叉树应用知识。构造最优二叉树的哈夫曼算法如下:①根据给定的n个权值{W1,W2,...,Wn},构成n棵二叉树的集合F={T1,T2,...,Tn},其中每棵二叉树Ti中只有一个带权为Wi的根结点,其左右子树均空。②在F中选取两棵权值最小的二叉树作为左、右子树构造一棵新的二叉树,置新构造二叉树的根结点的权值为其左、右子树根结点的权值之和。③从F中删除这两棵树,同时将新得到的二叉树加入到F中。重复②、③,直到F中只含一棵树时为止。这棵树便是最优二叉树(哈夫曼树)。根据题中给出的权值集合,构造哈夫曼树的过程如下图所示。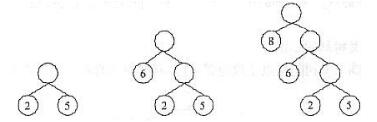
-
第5题:
对n(n≧2)个权值不同的字符依哈夫曼算法构造哈夫曼树,下面关于该哈夫曼树的叙述中错误的是 。
A.树中一定没有度为1的结点
B.该树一定是一棵完全二叉树
C.树中两个权值最小的结点一定是兄弟结点
D.树中任何一个非叶结点的权值一定不小于下一层任意一个结点的权值
该树一定是一棵完全二叉树
