—项工程，甲、乙合作12天完成，乙、丙合作9天完成，丙、丁合作12天完成，如果甲、丁合作，则完成这项工程需要的天数是： A.16 B.18 C.24 D.26

题目
—项工程，甲、乙合作12天完成，乙、丙合作9天完成，丙、丁合作12天完成，如果甲、丁合作，则完成这项工程需要的天数是：

A.16
B.18
C.24
D.26
相似考题

1.一件工程,甲乙两人合作36小时完成,乙丙两人合作45小时完成,甲丙两人合作要60小时完成,问甲单一件工程，甲乙两人合作３６小时完成，乙丙两人合作45小时完成，甲丙两人合作要60小时完成，问甲单独做需要多少小时完成？A.72B.75C.81D.90

2.一项工程，甲一人做完需30天，甲、乙合作完成需18天，乙、丙合作完成需15天。甲、乙、 丙三人共同完成该工程需（ ）。 A. 10 天 R 12 天 C. 8 天 D. 9 天

3.甲、乙、丙三人共同完成一项工程，他们的工作效率之比是5:4:6，先由甲、乙两人合作6天，再由乙单独做9天， 完成全部工程的60%，若剩下的工程由丙单独完成，则丙所需要的天数是?A.10 B.12 C.9 D.15

4.师徒三人合作承包一项工程，4天能够全部完成．已知师傅单独做所需要的天数与毳个徒弟合作所需要的天数相等，师傅与甲徒弟合作所需天数的2倍与乙徒弟单独完成这项工程所需的天数相等．那么甲徒弟单独做，完成这项工程需要多少天？( )A．12B．18C．20D．24

更多“—项工程，甲、乙合作12天完成，乙、丙合作9天完成，丙、丁合作12天完成，如果甲、丁合作，则完成这项工程需要的天数是： ”相关问题

  • 第1题：

    某项工程若由甲、乙两队合作需105天完成，甲、丙两队合作需60天，丙、丁两对合作需70天，甲、丁两对合作需84天。问这四个工程的工作效率由低到高的顺序是什么：
    A乙丁甲丙
    B乙甲丙丁
    C丁乙丙甲
    D乙丁丙甲


    答案：A
    解析：
    解析
    根据题干条件，甲丙合作需要60天，甲丁合作需要84天，甲的工作效率一定，故可推知丙的效率要高于丁的效率，由此排除B项；丙丁合作需要70天，甲丁合作需要84天，同理可以推知，丙的效率应高于甲的效率，由此排除C、D，只有A项符合。
    故正确答案为A。

  • 第2题：

    有一项工程，甲、乙、丙合作一天完成了工程的5/6，已知甲、乙、丙单独完成这项工程所用时间均为整数天数，且甲单独完成这项工程所用天数大于乙，乙所用天数大于丙，问甲、乙合作完成整个工程需要几天？

    A.3
    B.4
    C.5
    D.6

    答案：A
    解析：
    第一步，本题考查工程问题，属于时间类，用赋值法解题。
    第二步，结合题意赋总量为12，由“甲、乙、丙合作一天完成了工程的”，可知效率有：甲＋乙＋丙＝12×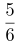＝10①，由“甲、乙、丙单独完成这项工程所用时间均为整数天数”，可得：12÷甲 ②、12÷乙③、12÷丙④均为整数，由②③④可得甲、乙、丙效率可能的取值为1、2、3、4、6等，由①及“甲单独完成这项工程所用天数大于乙，乙所用天数大于丙”，得效率：甲＝1，乙＝3，丙＝6满足题意。
    第三步，甲、乙合作完成整个工程需要＝3（天）。
    因此，选择A选项。

  • 第3题：

    某市有甲、乙、丙三个工程队，有一个工程需要三个工程队合作完成，已知甲队单独完成这 项工程需要10天，乙队单独完成这项工程需要8天，丙队单独完成这项工程需要15天。现三队合作，但甲队因故只参加了 3天，丙队也休息了若干天，最后该工程用了4天完成， 则丙队休息的天数是（ ）。

    A. 1
    B. 2
    C. 3
    D.4

    答案：B
    解析：
    本题可以采用赋值法。设工程总量为甲、乙、丙三个工程队单独完成工作时间的最小公倍数120，则甲队的效率为12，乙队的效率为15，丙队的效率为8。设丙队休息的天数为x，则根据题意列方程如下：12×3 + 15×4 + 8(4-x) = 120，解得x=1，答案选A。

  • 第4题：

    有一项工程，甲、乙、丙合作一天完成了工程的5/6，已知甲、乙、丙单独完成这项工程所用时间均为整数天数，且甲单独完成这项工程所用天数大于乙，乙所用天数大于丙，问甲、乙合作完成整个工程需要几天？

    A.3
    B.4
    C.5
    D.6

    答案：A
    解析：

  • 第5题：

    一项工程，甲一人做完需30天，甲、乙合作完成需18天，乙、丙合作完成需15天，甲、乙、丙三人共同完成该工程需（）

    • A、10天
    • B、12天
    • C、8天
    • D、9天

    正确答案:A

  • 第6题：

    单选题
    现有一项工程需要甲、乙、丙三个工程队去完成，已知甲、乙两队合作需要10天，甲、丙两队合作需要12天，乙、丙两队合作需要15天，则三队共同合作完成需要多少天？
    A

    5

    B

    6

    C

    7

    D

    8


    正确答案： B
    解析：

  • 第7题：

    现由甲、乙、丙三人完成一项工程，如果由甲、乙两人合作，需要12小时完成；如果由乙、丙两人合作，需要l0小时完成；如果甲、乙、丙三人合作，需要6小时才能完成，则这项工程如果全部由甲单独完成，所需小时数为（　　）。

    A.15
    B.18
    C.20
    D.25

    答案：A
    解析：
    由题意知，甲、乙、丙三人合作需6小时完成，乙、丙两人合作需10小时完成，则甲单独
    {图}

  • 第8题：

    一份文稿甲、乙、丙、丁合作 5 天完成录入，现在四人合作 2 天后，甲和丁有事被调走，乙、丙继续合作 5 天后完成录入，如该文稿仅由甲和丁两人一起录入需要（ ）天才能完成。

    A.12
    B.12.5
    C.13
    D.13.5

    答案：B
    解析：
    由题干可知，乙、丙合作 5 天的工作量＝四人合作 3 天的工作量，即甲、丁合作 3 天的工 作量＝乙、丙合作 2 天的工作量，那么乙、丙合作 5 天的工作量由甲、丁完成需要 5÷2×3＝7.5 天，则若该文稿仅由 甲和丁两人录入需要 7.5＋5＝12.5 天。

  • 第9题：

    某工程由甲、乙两工程队合作需要10天完成，乙、丙两个工程队合作需要7天完成，甲、乙、丙三个工程队合作需要5天完成。现甲、乙、丙三个工程队同时工作，2天后，乙工程队因有其他任务撤离该工程，问甲、丙两个工程队还需多少天能完成该工程？（ ）

    A.3
    B.4
    C.5
    D.6

    答案：B
    解析：
    设工程总量为70，则甲的效率+乙的效率=70÷10=7，乙的效率+丙的效率=70÷7=10,甲的效率+乙的效率+丙的效率=70÷5=14，则甲的效率=14－10=4，丙的效率=14－7=7。甲、乙、丙前两天共同完成的工作量=14×2=28，剩余工作量=70－28=42。甲、丙同时完成剩余工作量需要天数=42÷(4+7)≈3.8(天），故答案为B。

  • 第10题：

    有一项工程，甲、乙、两合作一天完成了工程的5/6，已知甲、乙、丙单独完成这项工程所用时间均为整数天数，且甲单独完成这项工程所用天数大于乙，乙所用天数大于丙，问甲、乙合作完成整个工程需要几天？

    A.3
    B.4
    C.5
    D.6

    答案：A
    解析：
    本题考查工程问题。
    赋值工程总量为6，三人效率分别是甲、乙、丙，则甲+乙+丙=6×
    5/6=5，又知完成这项工程所用的时间t甲＞t乙＞t丙且都为整数，只有当甲、乙、丙的时间是6的约数6天、2天、1天的n倍时，效率和=
    6/6n+6/2n+6/n=10/n才能是5的倍数，可知n=2，则甲、乙、丙的工作效率为0.5、1.5、3。则甲乙合作完成该工程需要6/（1.5+0.5）=3（天）。
    故本题的正确答案为A项。

  • 第11题：

    某市有甲、乙、丙三个工程队，有一个工程需要三个工程队合作完成，已知甲队单独完成这项工程需要10天，乙队单独完成这项工程需要8天，丙队单独完成这项工程需要15天。现三队合作，但甲队因故只参加了3天，丙队也休息了若干天，最后该工程用了4天完成，则丙队休息的天数是（）

    • A、1
    • B、2
    • C、3
    • D、4

    正确答案:A

  • 第12题：

    单选题
    一项工程，甲一人做完需30天，甲、乙合作完成需18天，乙、丙合作完成需15天，甲、乙、丙三人共同完成该工程需（　　）。
    A

    10天

    B

    12天

    C

    8天

    D

    9天


    正确答案： A
    解析：
    将总工程量赋值为90，则甲效率为90÷30＝3，甲、乙合作的效率为90÷18＝5，乙的效率为2；而乙、丙合作的效率为90÷15＝6，丙的效率为4。甲、乙、丙效率之和为9，三人合作该工程需要90÷9＝10天。

相关内容