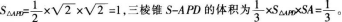（Ⅱ）设线段CD、AE的中点分别为P、M，求证：PM∥平面BCE；

题目

（Ⅱ）设线段CD、AE的中点分别为P、M，求证：PM∥平面BCE；

相似考题

1.（Ⅱ）设M为线段DE的中点，求直线FM与平面A′DE所成角的余弦值．

2.如图，在四边形ABCD中，∠ABC=90°，CD⊥AD，AD2+CD2=2AB2.(1)求证：AB=BC； (2)当BE⊥AD于E时，试证明：BE=AE+CD.

3.已知两个共用一个顶点的等腰Rt△ABC，等腰Rt△CEF，∠ABC=∠CEF= 90o，连接AF，M是AF的中点，连接MB，ME。 (1)如图1，当CB与CE在同一直线上时，若CB=a，CE=2a，求BM，ME的长； (2)如图2,当∠BCE=45o时，求证：BM=ME。

4.在四边形ABCD中,△ABD,△BCD,△ABC的面积比是3:4:1,点M,N分别在AC,CD上,满足AM:AC=CN:CD,并且B,M,N共线,求证:M与N分别是AC和CD的中点。

更多“(Ⅱ)设线段CD、AE的中点分别为P、M,求证:PM∥平面BCE; ”相关问题

  • 第1题：

    如图，三棱柱ABC-A1B1C1，M，N分别为AB，B1C1的中点，
    (1)求证MN∥平面AA1C1C；
    (2)若C1C=CB1，CA=CB，平面CC1B1B⊥平面ABC，求证：AB⊥平面CMN。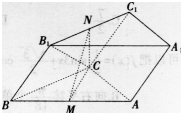


    答案：
    解析：

  • 第2题：

    在直角三角形ABC中，点D是斜边AB的中点，点P为线段CD的中点，则( )。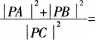

    A、2
    B、4
    C、5
    D、10

    答案：D
    解析：
    本题主要考查两点问的距离公式，以及坐标法这一重要的解题方法和数形结合的数学思

  • 第3题：

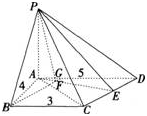
    如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AB=4，BC=3，AD=5，∠DAB=∠ABC=90o，E是CD的中点。
    (1)证明：CD⊥平面PAE；
    (2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等，求四棱锥P-ABCD的体积。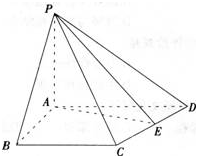


    答案：
    解析：



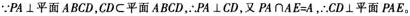
  • 第4题：

    设曲线y=y（x）过（0，0）点，M是曲线上任意一点，MP是法线段，P点在x轴上，已知MP的中点在抛物线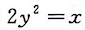，求此曲线的方程。


    答案：
    解析：

  • 第5题：

    如图，四棱锥S-ABCD的底面是矩形，SA⊥底面ABCD，P是BC边的中点，AD=2，SA=AB=1。



    (1)求证：PD⊥平面SAP；
    (2)求三棱锥S-APD的体积。


    答案：
    解析：
    (1)证明：易知在△APD中，，AD=2，满足勾股定理，故PD⊥AP。SA⊥底面ABCD，则SA⊥PD。PD同时垂直于平面SAP内的两条相交直线，PD⊥平面SAP。 (2)

相关内容