辽宁省大连市第二十九中学八年级数学上学期晨测卷5无答案新人教版
(6分)如图,点P为矩形ABCD边BC上一点(不包括端点),E为BC延长线上一点,CQ为∠DCE的角平分线,连接AP,PQ,使AP⊥PQ。求证:当AB=BC时,存在AP=PQ。


答案:
解析:
∴AP=PQ。


∴AP=PQ。

如图:已知圆0,点P在圆外,D,E在圆上,PE交圆于C,PD与圆相切,G为CE上一点且满足PG=PD,连接DG并延长交圆于A,作弦AB⊥EP,垂足为F。

(1)求证:AB为圆的直径;
(2)若AC=BD,AB=5,求弦DE的长。

(1)求证:AB为圆的直径;
(2)若AC=BD,AB=5,求弦DE的长。
答案:
解析:
(1)证明:∵PG=PD,∴∠PGD=∠PDG,又∵∠AGF=∠PGD,∠PDG=∠ABD,∴∠AGF=∠ABD,∴∠ADB=∠AFP=90°,∴AB为圆的直径。
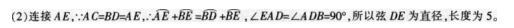
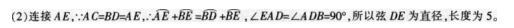
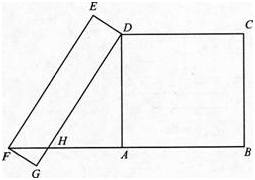
如图,四边形ABCD与四边形DEFG都是矩形,顶点F在BA的延长线上,边DG与AF交于点H,AD=4,DH=5,EF=6,求FG的长.

答案:
解析:
解:∵四边形ABCD和四边形DEFG均为矩形,
∴∠DAF=∠DAB=90°,∠G=90°,DG=EF.
∵EF=6,DH=5,∴GH=DG-DH=EF-DH=6-5=1
在Rt△ADH中,AD=4,DH=5,
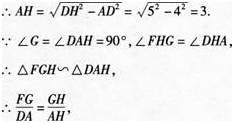

∴∠DAF=∠DAB=90°,∠G=90°,DG=EF.
∵EF=6,DH=5,∴GH=DG-DH=EF-DH=6-5=1
在Rt△ADH中,AD=4,DH=5,

如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.

(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.

(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
答案:
解析:







如图,边长为a的正方形ABCD中,点E是对角线BD上的一点,且BE=BC,点P在EC上,PM⊥BD于M,PN⊥BC于N,则PM+PN=________。


答案:
解析:
解析:作EK⊥BC于K,连接BP,由△EBC的面积等于△PBE和△PBC的面积之和且BE=



解析:作EK⊥BC于K,连接BP,由△EBC的面积等于△PBE和△PBC的面积之和且BE=


级数学晨测1、如图,点E、F在BC上,BE=CF,AB=AC,B=C.求证:BAF=CAE.2、如图,点B,F,C,E在一条直线上,FB=CE,ABED,ACFD,求证:AB=DE,AC=DF.3、如图,AB=CD,AEBC,DFBC,垂足分别为E,F,CE=BF.求证:AE=DF.4、如图,1=2,B=D.求证:AB=CD.5、已知:BD、CE是ABC的高,点P在BD的延长线上,BP=AC,点Q在CE上,CQ=AB.判断线段AP和AQ的关系,并加以证明.1
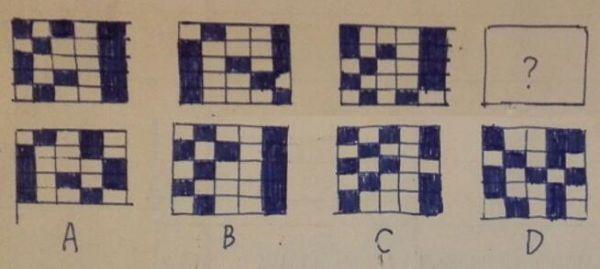
A. 如图所示,选A
B. 如图所示,选B
C. 如图所示,选C
D. 如图所示,选D
B. 如图所示,选B
C. 如图所示,选C
D. 如图所示,选D
答案:A
解析:
题干中图形,中间部分全部只有两个黑块,且黑块的位置不重叠,。因此,正确答案是A选项。
A. 如图所示,选A
B. 如图所示,选B
C. 如图所示,选C
D. 如图所示,选D
B. 如图所示,选B
C. 如图所示,选C
D. 如图所示,选D
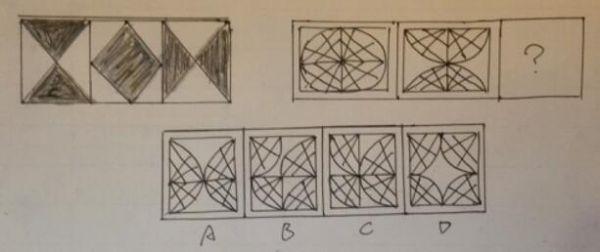
答案:D
解析:
题干中第一组可分为四个部分,各部分分别先上下翻转,后左右翻转。第二组先上下翻转后左右翻转。因此,正确答案是D选项。
A. 如图所示,选A
B. 如图所示,选B
C. 如图所示,选C
D. 如图所示,选D
B. 如图所示,选B
C. 如图所示,选C
D. 如图所示,选D
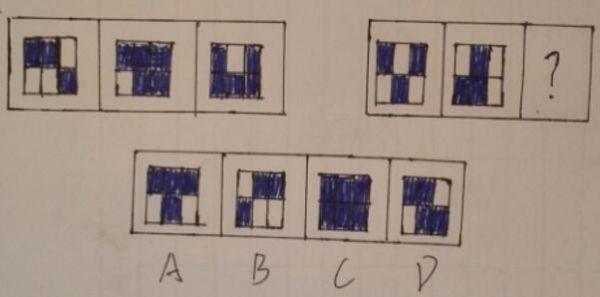
答案:B
解析:
题干中黑色部分数量为3、5、5,3、3、?,都为奇数个,因此正确答案为B选项。
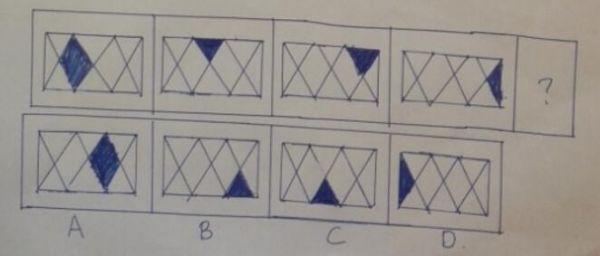
A. 如图所示,选A
B. 如图所示,选B
C. 如图所示,选C
D. 如图所示,选D
B. 如图所示,选B
C. 如图所示,选C
D. 如图所示,选D
答案:A
解析:
本题考查的是黑色方块的移动规律,1,2,1,2,1
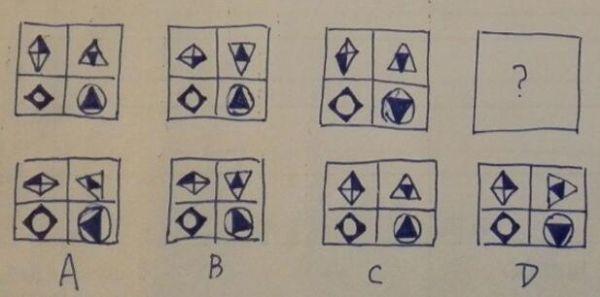
A. 如图所示,选A
B. 如图所示,选B
C. 如图所示,选C
D. 如图所示,选D
B. 如图所示,选B
C. 如图所示,选C
D. 如图所示,选D
答案:B
解析:
题干中左上角图形做旋转,且内部黑色位置顺时针移动,右上角图形上下一次翻转,左下角不变,右下角每次顺时针旋转45°。按照此规律,正确答案是B选项。
更多 “辽宁省大连市第二十九中学八年级数学上学期晨测卷5无答案新人教版” 相关考题
考题
如图,已知四棱锥P-ABCD底面ABCD为矩形,侧棱PA⊥ABCD,AB=AP=21/2AD=2,E,F分别为PC,AB的中点。
(I)证明:EF∥面PAD。
(II)求三棱锥B-PFC的体积。
答案:解析:
考题
(10分)如图,四棱锥P-ABCD的底面为正方形,侧棱PD⊥底面ABCD,点E为棱PA的中点,PD=AD=1。
(1)求证:PC∥平面BDE:
(2)求三棱锥B-PDE的体积。
答案:解析:(1)如图所示,连接AC,AC与BD交于点M,连接EM。因为底面ABCD是正方形,所以M为AC中点,又因为E为PA中点,所以
考题
A. 如图所示,选A
B. 如图所示,选B
C. 如图所示,选C
D. 如图所示,选D答案:B解析:题干中相邻图形之间线条变化数量分别为1、2、3、4,同时,右上角每次顺时针旋转90°,右下角每次逆时针旋转90°左下角每次顺时针90°,按照此规律。因此,正确答案是B选项。
考题
如图,在直三棱柱ABC—A1B1C1中,E,F分别是A1B,A1C的中点,点D在B1C,上,A1D⊥B1C,求证:(8分)
(1)EF∥平面ABC;
(2)平面A1FD上平面BB1C1C.
答案:解析:证明:(1)由E,F分别是A1B1A1C的中点知,EF∥BC,
考题
如图,正方体ABCD-A1B1C1D1中,E,F,G分别为AA1,A1D1,BC的中点,则异面直线EF与D1G所成角的大小为__________。 答案:解析:连接AD1,AG,由于EF平行于AD1,则异面直线EF与D1G所成角等于AD1与D1G所成角。设正方体棱长为2,在△AD1G中,D1G=3,根据余弦定理,cos∠AD1G=
考题
A. 如图所示,选A
B. 如图所示,选B
C. 如图所示,选C
D. 如图所示,选D答案:B解析:题干中左上角图形做旋转,且内部黑色位置顺时针移动,右上角图形上下一次翻转,左下角不变,右下角每次顺时针旋转45°。按照此规律,正确答案是B选项。
考题
如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P是BC边的中点,AD=2,SA=AB=1。 (1)求证:PD⊥平面SAP;
(2)求三棱锥S-APD的体积。 答案:解析:(1)证明:易知在△APD中,,AD=2,满足勾股定理,故PD⊥AP。SA⊥底面ABCD,则SA⊥PD。PD同时垂直于平面SAP内的两条相交直线,PD⊥平面SAP。 (2)
考题
A. 如图所示,选A
B. 如图所示,选B
C. 如图所示,选C
D. 如图所示,选D答案:A解析:题干中图形,中间部分全部只有两个黑块,且黑块的位置不重叠,。因此,正确答案是A选项。
考题
A. 如图所示,选A
B. 如图所示,选B
C. 如图所示,选C
D. 如图所示,选D答案:B解析:本题只有两种元素,黑圈和白圈,观察选项中的黑圈白圈个数存在不同,考虑数数。题干中除了问号处,已知相连黑圈的个数分别为1,2,X,X,5,由此可知,与选项结合后的最终图形中,中间两个X应该分别有3个黑圈相连和4个黑圈相连,而题干问号前后已经各有两个黑圈,选择的选项中左端应该有1个黑圈,右端有2个,只能选B。将B代入整体观察后,发现相连的白圈个数也满足等差数列依次递减的规律,分别是5、4、3、2、1。故正确答案为B选项。
相关内容
最新试卷
热门试卷
- 2021年10月24日安徽宿州砀山县事业单位考试含解析_
- 2021年4月17日四川眉山市属事业单位招聘考试《公共基础知识》试题_
- 2021年安徽合肥庐阳区事业单位考试《综合知识》试题含答案_
- 2021年5月22日安徽事业单位统考笔试专业科目试题(法律类)含答案_
- 2021年6月26日成都市属事业单位《职业能力倾向测验》试题含答案_
- 2021年4月上海事业单位招聘考试《职业能力倾向测验》试题含答案_
- 2021年1月陕西西安社区工作者招聘笔试试题含答案_
- 2021年5月23日天津事业单位联考《综合知识》(文字综合岗)含答案_
- 2021年4月11日陕西事业单位中小学教师招聘考试《职业能力倾向测试》题含答案_
- 2021年山东公务员考试《申论》试题(A,b类)_
