如图,已知四棱锥P-ABCD底面ABCD为矩形,侧棱PA⊥ABCD,AB=AP=21/2AD=2,E,F分别为PC,AB的中点。 (I)证明:EF∥面PAD。 (II)求三棱锥B-PFC的体积。
题目
如图,已知四棱锥P-ABCD底面ABCD为矩形,侧棱PA⊥ABCD,AB=AP=21/2AD=2,E,F分别为PC,AB的中点。
(I)证明:EF∥面PAD。
(II)求三棱锥B-PFC的体积。
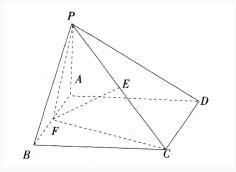
(I)证明:EF∥面PAD。
(II)求三棱锥B-PFC的体积。

相似考题
更多“如图,已知四棱锥P-ABCD底面ABCD为矩形,侧棱PA⊥ABCD,AB=AP=21/2AD=2,E,F分别为PC,AB的中点。 ”相关问题
-
第1题:
(6分)如图,点P为矩形ABCD边BC上一点(不包括端点),E为BC延长线上一点,CQ为∠DCE的角平分线,连接AP,PQ,使AP⊥PQ。求证:当AB=BC时,存在AP=PQ。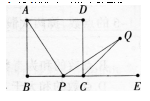 答案:解析:
答案:解析:
∴AP=PQ。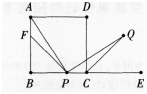
-
第2题:
如图,P是矩形ABCD内一点,若PA=3,PB=4,PC=5,则PD=_______。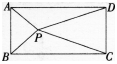 答案:解析:
答案:解析:
解析:矩形内的点到相对顶点的距离平方和相等,即PA2+PC2=PB2+PD2,即32+52=42+PD2,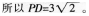
-
第3题:
如图,平面四边形ABCD中,AB=2,BC=4,CD=5,DA=3,
(1)若∠B与∠D互补,求AC2的值;
(2)求平面四边形ABCD面积的最大值。 答案:解析:
答案:解析: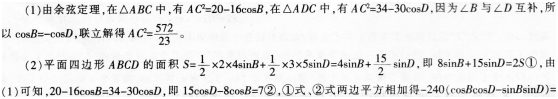
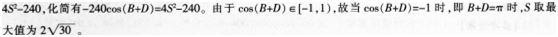
-
第4题:
如图所示,矩形ABCD的面积为1,E、F、G、H分别为四条边的中点,FI的长度是IE的两倍,问阴影部分的面积为多少?

 答案:B解析:解题指导: 作辅助线。连接FG、EH。那么平行四边形EFGH的面积为矩形ABCD的一半,三角形GIH的面积又是平行四边形EFGH面积的一半,所以因应面积为1/4。故答案为B。
答案:B解析:解题指导: 作辅助线。连接FG、EH。那么平行四边形EFGH的面积为矩形ABCD的一半,三角形GIH的面积又是平行四边形EFGH面积的一半,所以因应面积为1/4。故答案为B。 -
第5题:
如图,ABCD为矩形,AB=4,BC=3,边CD在直线L上,将矩形ABCD沿直线L作无滑动翻转,当点A第一次翻转到点A1位置时,点A经过的路线长为: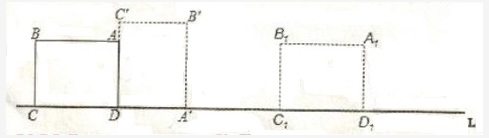
A7π
B6π
C3π
D3π/2答案:B解析:
-
第6题:
已知正六棱锥的底面边长为3,侧棱长为5,则该六棱锥的体积为() 答案:A解析:
答案:A解析: -
第7题:
如 ,正方体ABCD-A′B′C′D′的棱长为2,F是棱C′D′的中点,则AF的长为
,正方体ABCD-A′B′C′D′的棱长为2,F是棱C′D′的中点,则AF的长为
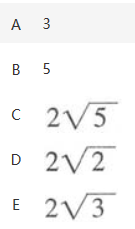 答案:A解析:
答案:A解析:
-
第8题:
(10分)如图,四棱锥P-ABCD的底面为正方形,侧棱PD⊥底面ABCD,点E为棱PA的中点,PD=AD=1。
(1)求证:PC∥平面BDE:
(2)求三棱锥B-PDE的体积。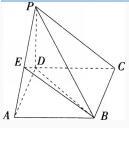 答案:解析:(1)如图所示,连接AC,AC与BD交于点M,连接EM。因为底面ABCD是正方形,所以M为AC中点,又因为E为PA中点,所以
答案:解析:(1)如图所示,连接AC,AC与BD交于点M,连接EM。因为底面ABCD是正方形,所以M为AC中点,又因为E为PA中点,所以

-
第9题:
已知四棱锥P-ABCD底面为直角梯形,AB平行于DC,∠DAB=90°,PA垂直于底面ABCD,PA=AD=DC=

AB=1,M为PB中点。
(1)求证:面PAD⊥面PCD;
(2)求面AMC与面BMC所成二面角的余弦值。答案:解析:(1)∵PA⊥面ABCD,CD⊥AD, ∴由三垂线定理,得CD⊥PD。
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴CD⊥面PAD。
又CD面PCD,∴面PAD⊥面PCD。
(2)作AN⊥CM,垂足为N,连结BN。
在Rt△PAB中,∵M是斜边PB中点,
∴AM=MB.

-
第10题:
已知正六棱锥底面的边长为2cm,侧棱长4cm求正六棱锥的体积?
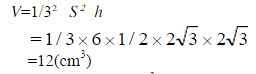
略 -
第11题:
已知圆内接四边形ABCD中,AB、CD的延长线交与点F,则F=()
- A、40°
- B、50°
- C、60°
- D、70°
正确答案:A -
第12题:
单选题字符串()是“abcd321ABCD”的子串。A“21AB”
B“abcD”
C“aBCD”
D“321a”
正确答案: B解析: 暂无解析 -
第13题:
在平行四边形ABCD中,∠DAB=60,AB=15cm,已知圆O的半径等于3cm,AB,AD分别与圆O相切于点E,F.圆0在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止.试求圆O滚过的路程.答案:解析:
-
第14题:
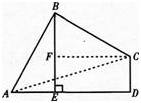
如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.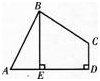
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.答案:解析: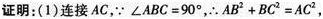
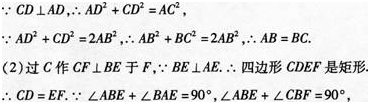

-
第15题:
如图,在矩形ABCD中,AB=5,BC=12,将矩形ABCD沿对角线对折放在桌面上,折叠后所成的图形覆盖桌面的面积是 答案:解析:
答案:解析:
解析:

-
第16题:
如图所示,矩形ABCD的面积为1,E、F、G、H分别为四条边的A 中点,FI的长度是IE的两倍,问阴影部分的面积为多 少?( )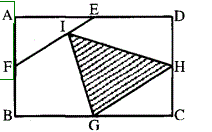
 答案:B解析:这个题目需要做辅助线,连接FG、EH。
答案:B解析:这个题目需要做辅助线,连接FG、EH。
因为E、F、G、H分别为四条边的中点,则平行四边形EFGH的面积是矩形ABCD面积的 1/2,而三角形IGH的面积是平行四边EFGH面积的1/2,所以阴影部分的面积为1/4。 -
第17题:
如图,正方体ABCD-A1B1C1D1的棱长为1cm,则三棱锥C-AB1D1的体积是: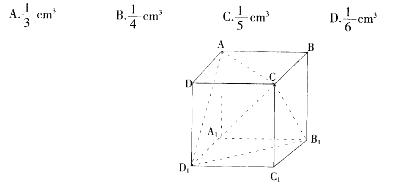 答案:A解析:
答案:A解析:
-
第18题:
四棱锥P-ABCD(如图7-12所示),用4种不同的颜色涂在四棱锥的各个面上,要求相邻不同色,有( )种涂法.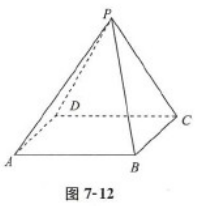 A.40
A.40
B.48
C.60
D.72
E.90答案:D解析: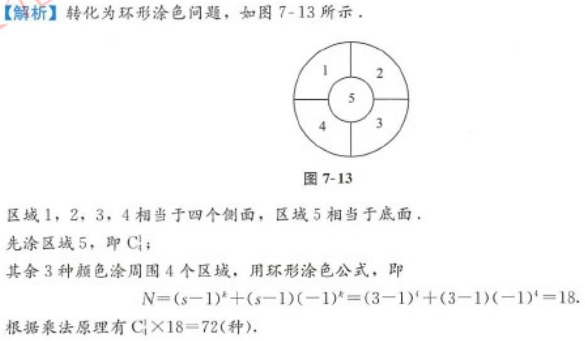
-
第19题:
如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=6,BC=8, AB∥DE,求△DEC的周长。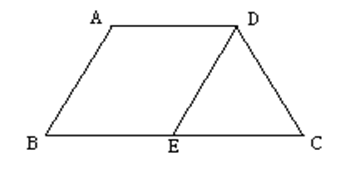 答案:解析:15
答案:解析:15 -
第20题:
如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P是BC边的中点,AD=2,SA=AB=1。

(1)求证:PD⊥平面SAP;
(2)求三棱锥S-APD的体积。答案:解析:(1)证明:易知在△APD中,,AD=2,满足勾股定理,故PD⊥AP。SA⊥底面ABCD,则SA⊥PD。PD同时垂直于平面SAP内的两条相交直线,PD⊥平面SAP。 (2)
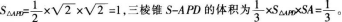
-
第21题:
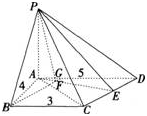
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90o,E是CD的中点。
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积。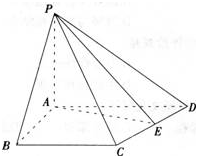 答案:解析:
答案:解析:
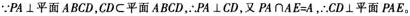

-
第22题:
逻辑代数式子f=AB+ABC+AB(C+D),则f的简化式子为()。
- A、AB
- B、A+B
- C、ABC
- D、ABCD
正确答案:A -
第23题:
字符串()是“abcd321ABCD”的子串。
- A、“21AB”
- B、“abcD”
- C、“aBCD”
- D、“321a”
正确答案:A