高中数学教师资格证面试真题

数列是高中数学很重要的内容之一，数列中求通项的问题也是最常见的题型，其形式多样，解法灵活。请谈谈你认为的几种常用的求数列通项的方法。


正确答案：
纲要：举例说明，有：迭加法，迭乘法，换元法，倒数法，待定系数法，分类讨论等等(需简要说明每种方法适用的情况)。

已知等差数列{an}的首项与公差相等，{an）的前n项的和记作Sn，且S20=840．

（I）求数列{an}的首项a1及通项公式；

（Ⅱ）数列{an}的前多少项的和等于847.


正确答案：

已知数列{an}的前n项和Sn=n2-2n．求

（I）{an}的前三项；

（II）{an}的通项公式．


正确答案：

标准等差数列的计算公式为(row(a1)－1)*公差。()

此题为判断题(对，错)。


答案：正确

已知等差数列前n项和
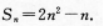
(Ⅰ)求这个数列的逋项公式；
(II)求数列第六项到第十项的和．


答案：
解析：

摘要:2017下高中数学《等差数列的通项公式》

已知等比数列{an}的各项都是正数，且a1+a3=10，a2+a3=6．
(I)求{an}的通项公式；
(II)求{an)的前5项和．


答案：
解析：

已知等比数列{an}的各项都是正数，且a1+a3=10，a2+a3=6．
(Ⅰ)求{an}的通项公式；
(Ⅱ)求{an}的前5项和．


答案：
解析：
解:(Ⅰ)设(an)的公比为q，由已知得

已知一个等差数列的第五项等于10，前三项的和等于3，那么这个等差数列的公差为（ ）

A.3
B.1
C.-1
D.-3

答案：A
解析：

已知数列{an｝中，Sn是它的前n项和，并且Sn+1=4an+2,a1=1．
(Ⅰ)设bn=an+1-2an，求证：数列{bn)是等比数列；
(Ⅱ)设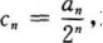求证：数列{cn}是等差数列；
(Ⅲ)求数列｛an｝的通项公式及前n项和．


答案：
解析：



已知数列{an}的通项公式为an=2n,数列{bn}的通项公式为bn=3n+2.若数列{an}和{bn}的公共项顺序组成数列{cn},则数列{cn}的前3项之和为（ ）

A.248
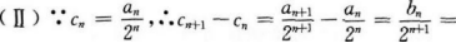
B.168
C.128
D.19
E.以上选项均不正确

答案：B
解析：

更多 “高中数学教师资格证面试真题” 相关考题
考题 高中数学《等比数列前n项和》 一、考题回顾 题目来源：5月19日 上午 重庆市 面试考题 试讲题目 1.题目：等比数列前n项和 2.内容：3.基本要求： (1)引导学生应用等比数列前n项和; (2)试讲10分钟; (3)合理设计板书; (4)要有适当的提问互动环节。 答辩题目 1.等差数列的前n项和公式是什么? 2.怎样才能设计好授课板书呢?你能给出几点建议吗?答案：解析：二、考题解析 【教学过程】 (一)引入新课 复习等差数列前n项和公式。提问：等比数列前n项和怎么求呢?有没有相应的公式呢? 引出课题。 (二)探索新知
查看答案
考题 多选题列入高中数学课程数列内容是：（）A等差数列B差分数列C递归数列正确答案：A,B解析：暂无解析
查看答案
考题 (10分)已知数列{an}满足a1=3，an+1= an +2n， (1)求{ an }的通项公式an； (2)若bn=n an，求数列{bn}的前n项和sn。 答案：解析：
查看答案
考题 多选题列入高中数学课程数列内容是：（）A等差数列B差分数列C递归数列正确答案：A,B解析：暂无解析
查看答案
考题 单选题以下属于二阶递推公式的是（）。A 圆的面积公式B 等差数列C 等比数列D 斐波那契数列正确答案：D解析：暂无解析
查看答案
考题 已知数列(1)求证：数列是等差数列： (2)求数列的通项公式。 答案：解析：(2)数列
查看答案
考题 已知数列{an}满足a1=2，an+1=3an+2(n∈N*)， (1)求数列{an}的通项公式； 答案：解析：
查看答案
考题 在Excel 2010的填充功能不能实现（）操作。A、复制等差数列B、复制数据后公式到相邻单元格中C、填充等比数列D、复制数据后公式到不相邻得单元格中正确答案:D
查看答案
考题 案例：在等差数列的习题课教学中，教师布置了这样一个问题：等差数列前10项和为100，前100项和为10，求前110项的和。两位学生的解法如下：学生甲：设等差数列的首项为a1，公差为d，则学生乙：设等差数列针对上述解法，一些学生提出了自己的想法。（1）请分析学生甲和学生乙解法各自的特点，并解释学生乙设的理由。（12分） （2）请验证(*)中结论是否成立。答案：解析：本题主要从“等差数列”相关知识入手，考查等差数列的相关概念、等差数列的通项公式、求和公式等基层知识，教学工作的基本环节，常用的教学方法，以及课堂导入技巧等基本知识与技能。
查看答案
考题 高中数学《二项式定理》一、考题回顾二、考题解析 【教学过程】 (一)引入新课 提出问题：完全平方公式是如何展开的，你能在展开过程中发现什么运算规律? 师生活动：复习回顾完全平方公式的展开过程。 (二)探索新知答案：解析：
查看答案
相关内容
最新试卷
热门试卷