(10分)已知数列{an}满足a1=3，an+1= an +2n， (1)求{ an }的通项公式an； (2)若bn=n an，求数列{bn}的前n项和sn。

题目

(10分)已知数列{an}满足a1=3，an+1= an +2n，
(1)求{ an }的通项公式an；
(2)若bn=n an，求数列{bn}的前n项和sn。

相似考题

1.已知数列{an}满足an=3n+1(n为奇数，n∈N) 2n-2（n为偶数，n∈N）则a2·a3=（）。A．70B．28C．20D．8

2.从满足a1=a2=1，an+2=an+1+an(n≥1)的数列{an)中，依次抽出能被3整除的项组成数列{bn}，则b100是多少? A．a100 B．a200 C．a300 D．a400

3.已知公差为2的正整数等差数列为an，则该数列满足不等式7/16＜an/5＜398/9的所有项的和为（）A．12320B．12430C．12432D．12543

4.已知等差数列{an}的首项与公差相等，{an）的前n项的和记作Sn，且S20=840．（I）求数列{an}的首项a1及通项公式；（Ⅱ）数列{an}的前多少项的和等于847.

更多“(10分)已知数列{an}满足a1=3，an+1= an +2n， ”相关问题

第1题：

已知数列{an}中,a1=2,an+1=(1+an)/(1-an).记数列{an}的前n项的乘积为∏n,则∏2012=____.

参考答案1
第2题：

已知某企业工人日产量统计资料，如表3-4所示。
根据上述资料请回答：
上述变量数列属于( )。
A．单项变量分布数列
B．组距变量分布数列
C．连续变量数列
D．等距数列

正确答案：BCD
解析：题中，次数分布数列以变量值的一定变动范围为一组所形成，故属于组距变量数列；各组组距均为10，故属于等距数列；日产量为连续变量，故属于连续变量数列。
第3题：

已知某分布数列，如表3-2所示，则此数列属于( )。
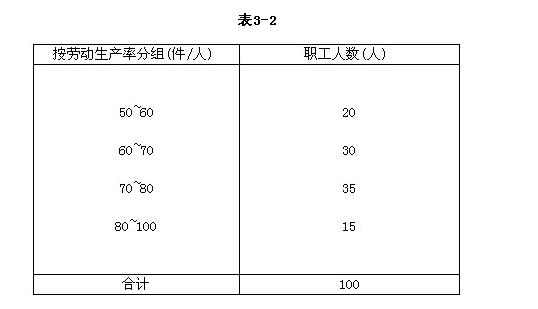
A．品质分布数列
B．变量分布数列
C．单项变量分布数列
D．组距变量分布数列
E．等距变量分布数列

正确答案：BD
解析：劳动生产率属于变量标志，故分布数列属于变量分布数列；按劳动生产率的一定变动范围为一组所形成的次数分布数列，且各组的组距不相等，故属于组距变量分布数列中的不等距变量分布数列，因此B、D项正确。
第4题：

已知等差数列{an}中，a1=21，Sn是它的前n项之和，S7=S15。
(1)求Sn；
(2)这个数列的前多少项之和最大求出最大值。

答案：
解析：
(1)设等差数列的公差为d，由题意可得：

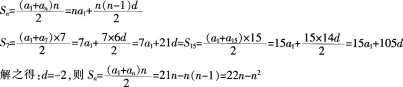
(2)Sn=22n-n2=-(n-11)2+121，当n=11时，数列之和最大，最大值为121。
第5题：

已知公差为2的正整数等差数列为an ，则该数列满足不等式7/16 ＜an/5 ＜398/9 的所有项的和为（）

A. 12320
B. 12430
C. 12432
D. 12543

答案：A
解析：
公差为2的正整数数列为奇数列，满足条件的an 最小为3，最大为221，故和为(3+22)*[(221-3)/2+1]/2=12320 。故答案为A。
第6题：

已知一等差数列a1，21，a3，31，…，an，…，若an=516，则该数列前n项的平均数是（）

A．266 B．258 C．255 D．212

答案：A
解析：
由等差数列的第2项和第4项可求出其公差d==5，则首项a1=21-5=16。又已知an=516，根据等差数列求和公式Sn==平均数×n，可得前n项的平均数为=266。
第7题：

已知数列{an｝中，Sn是它的前n项和，并且Sn+1=4an+2,a1=1．
(Ⅰ)设bn=an+1-2an，求证：数列{bn)是等比数列；
(Ⅱ)设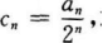求证：数列{cn}是等差数列；
(Ⅲ)求数列｛an｝的通项公式及前n项和．

答案：
解析：
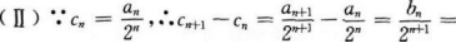
第8题：

已知数列a1，a2，a3……a10则a1-a2+a3-…+a9-a10≥0.（1）an≥an+1，n=1，2.…9（2）an2≥a2n+1，n=1，2…9

A.条件（1）充分，但条件（2）不充分
B.条件（2）充分，但条件（1）不充分
C.条件（1）和条件（2）单独都不充分，但条件（1）和条件（2）联合起来充分
D.条件（1）充分，条件（2）也充分
E.条件（1）和条件（2）单独都不充分，条件（1）和条件（2）联合起来也不充分

答案：A
解析：
第9题：

已知数列{an}满足a1=2，an+1=3an+2(n∈N*)，
(1)求数列{an}的通项公式；

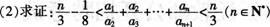答案：
解析：
第10题：

数列{a_n}满足a_n+1=a_n+2-a_n，a₁=2，a₂=5，则a₅为（）。
- A、-3
- B、-11
- C、19
- D、-5
正确答案:C
第11题：

单选题
数列{an}满足an+1=an+2-an，a1=2，a2=5，则a5为（）。
A
-3
B
-11
C
19
D
-5

正确答案： A
解析：暂无解析
第12题：

单选题
已知数列{an}满足an＋1＝an＋2，且a1＝1，那么它的通项公式an等于（　　）．
A
2n－1
B
2n＋1
C
2n－2
D
2n＋2

正确答案： D
解析：
由a_n_＋1＝a_n＋2可得a_n_＋1－a_n＝2，知数列{a_n}为等差数列，且公差d＝2，故通项公式为：a_n＝1＋（n－1）×2＝2n－1．
第13题：

已知某分布数列，如表3—2所示，则此数列属于（）。

正确答案：BD
劳动生产率属于变量标志，故分布数列属于变量分布数列；按劳动生产率的一定变动范围为一组所形成的次数分布数列，且各组的组距不相等，故属于组距变量分布数列中的不等距变量分布数列，因此B、D项正确。
第14题：

已知2000～2009年我国某地区粮食产量数据，如表3-5所示。根据上述资料请回答：
此数列属于( )。
A．时间数列
B．分布数列
C．动态数列
D．品质数列

正确答案：AC
解析：时间数列(动态数列)是一种统计数列，它是指将反映某一现象的统计指标在不同时间上的数值按时间先后顺序排列所形成的数列。
第15题：

已知某企业工人日产量资料，如表3—3所示。
根据以上资料请回答：
此数列属于( )。
A．单项式数列
B．品质数列
C．变量数列
D．等距数列

正确答案：CD
解析：题中“日产量”是数量标志，故此数列属于变量数列；每个组包含若干变量值，故属于组距数列，不属于单项式数列；组距相等，均为10，故属于等距数列。
第16题：

在等差数列{an}中，已知a1=2，且a2+a4=20，若an=18，则n=5。()

答案：对
解析：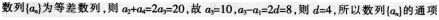
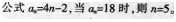
第17题：

设数列{an}满足条件：a0=3，a1=1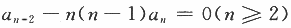，，S(x)是幂级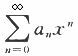数的和函数.
　　(Ⅰ)证明：S"(x)-S(x)=0；
　　(Ⅱ)求S(x)的表达式.

答案：
解析：
【分析】利用幂级数可逐项求导的性质，验证(Ⅰ)成立；解微分方程求出S(x)，注意初值条件的使用.
第18题：

已知等比数列a1=1，a9=25，则a5=（）

A.25
B.-5
C.±5
D.5

答案：C
解析：
第19题：

已知数列{an}的通项公式为an=2n,数列{bn}的通项公式为bn=3n+2.若数列{an}和{bn}的公共项顺序组成数列{cn},则数列{cn}的前3项之和为（）

A.248
B.168
C.128
D.19
E.以上选项均不正确

答案：B
解析：
第20题：

已知数列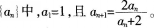(1)求证：数列是等差数列：
(2)求数列的通项公式。

答案：
解析：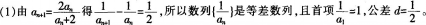
(2)数列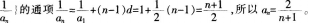
第21题：

(10分)已知数列{an}的前n项和Sn=2n+1-k(其中k为常数)：
(1)求数列{ an }的通项公式；(4分)
(2)若a1=2，求数列{n an }的前n项和Tn。(6分)

答案：
解析：
第22题：

问答题
（1）已知A1，A2同时发生时A发生，证明：P（A）≥P（A1）＋P（A2）－1。　　（2）已知任意三个事件A1，A2，A3都满足Ai⊂A（i＝1，2，3），证明：P（A）≥P（A1）＋P（A2）＋P（A3）－2。

正确答案：
(1)当A₁,A₂同时发生时A发生,所以A₁A₂⊂A,P(A)≥P(A₁A₂),因为P(A₁∪A₂)=P(A₁)+P(A₂)-P(A₁A₂),所以P(A₁A₂)=P(A₁)+P(A₂)-P(A₁∪A₂)。
又0≤P(A₁∪A₂)≤1,所以P(A)≥P(A₁A₂)≥P(A₁)+P(A₂)-1。
(2)因为A_i⊂A(i=1,2,3),所以A₁A₂A₃⊂A,由(1)结论可知,P(A)≥P(A₁A₂)+P(A₃)-1≥P(A₁)+P(A₂)-1+P(A₃)-1=P(A₁)+P(A₂)+P(A₃)-2。
解析：暂无解析
第23题：

单选题
已知等差数列{an}满足a2＋a4＝4，a3＋a5＝10，则它的前10项的和S10＝（　　）。
A
138
B
135
C
95
D
23

正确答案： D
解析：
由a₂＋a₄＝4，a₃＋a₅＝10得，a₁＝4，d＝3，故S₁₀＝10a₁＋45d＝40＋135＝95。

(10分)已知数列{an}满足a1=3，an+1= an +2n， (1)求{ an }的通项公式an； (2)若bn=n an，求数列{bn}的前n项和sn。

题目

相似考题

更多“(10分)已知数列{an}满足a1=3，an+1= an +2n， ”相关问题

相关内容