高中数学《二项式定理》一、考题回顾二、考题解析 【教学过程】 (一)引入新课 提出问题：完全平方公式是如何展开的，你能在展开过程中发现什么运算规律? 师生活动：复习回顾完全平方公式的展开过程。 (二)探索新知

第1题：

第2题：

高中数学《曲线与方程》

答案：

解析：

第3题：

答案：

解析：

第4题：

下列科技成就哪些是牛顿取得的（）①二项式定理②《关于光和色的新理论》③波动说④《自然哲学中的数学原理》

• A、①②③
• B、②③④
• C、①③④
• D、①②④

第5题：

下列关于高中数学基础性的说法不正确的是（）。

• A、高中数学课程为学生进一步学习提供了必要的数学准备
• B、高中数学课程为不同学生提供相同的基础
• C、高中数学课程体现时代性、基础性和选择性
• D、高中数学课程要以学生的发展为本，尊重他们的个性发展

第6题：

什么是二项式分布？

第7题：

关于牛顿的说法错误的是（）。

• A、发明了二项式定理
• B、发现了万有引力定律
• C、提出光的波动说
• D、发明了微积分

第8题：

（）的（）在《（）》一书中，提出指数为正整数的二项式定理系数表，史称“（）”，可以求出任意高次方程的数解值，这比欧洲阿皮纳斯的系数表要早400年。

第9题：

第10题：

第11题：

第12题：

第13题：

高中数学《余弦定理的证明》
一、考题回顾

答案：

解析：

二、考题解析
【教学过程】
(一)导入新课
情景导入：多媒体展示修路工人开凿山地隧道的情境图。提问：“为了测量山地隧道的长度，工人先在山顶选一个位置A，量出A点到隧道两端的距离AB、AC及AB与AC的夹角，最后算出隧道长度。哪位同学能说说这是一个什么数学问题?”
预设：已知三角形两边及其夹角，去求另一边的数学问题。
提问：“那工人们是如何算出来的呢?”
引发认知冲入，从而引出课题。



(四)小结作业
小结：通过这节课的学习，你有什么收获?
作业：课后题。
【板书设计】



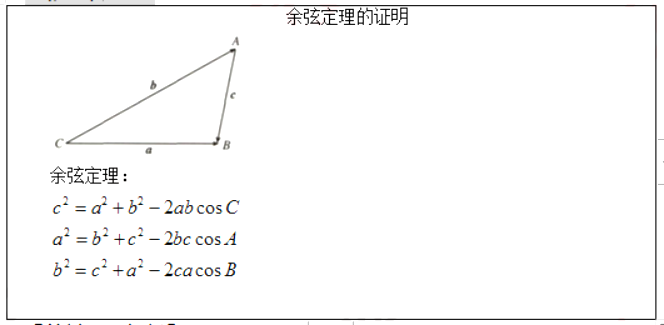
【答辩题目解析】
1.利用余弦定理可以解决哪几类解三角形的问题?
【参考答案】
(1)已知三边，求三个角。
(2)已知两边和夹角，求第三边和其他两个角。
2.如何备好一节课?
【参考答案】
一节好的数学课，要从以下几个方面准备：
首先，备教材，教材分析是教师备好课、上好课的基本保证，对教师顺利完成教学任务、提升教学质量有十分重要的意义。分析教材的过程既是教学科学把握教学内容、加深对教育理论的重要前提，更是教师进行教学研究的一种主要方法。
其次，备学生。教学的基本前提是为了学生而进行的教学，其根本目的在于促进学生的主动发展。因此在备课时要充分考虑所面对的学生特点。
最后，备教学方法。现代教学理论认为，在教学过程中，学生是学习的主体，教师是学习的组织者、引导者，教学的一切活动都必须以强调学生的主动性、积极性为出发点。

第14题：

第15题：

答案：

解析：

(1)看一看以下式子，展开式是什么有多少项



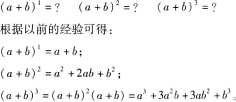
通过上面的等式，大家已经发现了一定的规律，展开式的首项和末项的系数均为1，中间项系数为其“肩上”的两个数字之和。



那么(a+b)n是否也有这样的规律呢你能准确写出这些项吗引出新课。
设计意图：通过这样的导入设计，首先创设情境，激发了学生的学习兴趣以及求知欲，有利于后续课堂的继续推进，另外在引导的过程中，先从简单的式子人手，再一步步深入，符合学生的认知经验，也为其在后续推导(a+b)n的过程中提供一定的方法和依据。
(2)推导二项式定理的基本步骤：




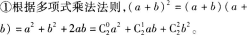
推导思路如下：(a+b)2是2个(a+b)相乘，根据多项式乘法法则，每个(a+b)在相乘时有两个选择，选a或选b，而且每个(a+b)中的a或b都选定后，才能得到展开式中的一项。于是由分步乘



③类比步骤②的推导思路，猜想(a+b)3，(a+b)4的展开式，并通过多项式乘法对猜想结果进行验证。



⑤对步骤④猜想的(a+b)n的展开式进行验证。类比步骤②中的推导思路，(a+b)n是n个(a+b)相乘，根据多项式乘法法则，每个(a+b)在相乘时有两个选择，选a或选b，而且每个(a+b)中的a或b都选定后，才能得到展开式中的一项。于是由分步乘法计数原理，在合并同类项之前，

第16题：

二项式定理对发现微积分方法起到了最直接的作用，著名的二项式定理是谁发明的（）

• A、莱布尼茨
• B、牛顿
• C、卡迪尔
• D、爱因斯坦

第17题：

下列关于高中数学课程结构的说法不正确的是（）。

• A、高中数学课程可分为必修与选修两类
• B、高中数学选修课程包括4个系列的课程
• C、高中数学必修课程包括5个模块
• D、高中课程的组合具有固定性，不能发生改变

第18题：

发现二项式定理的人是（）

• A、牛顿
• B、哥白尼
• C、伽利略
• D、开普勒

第19题：

二项式定理是谁发明的（）

• A、牛顿
• B、莱布尼茨
• C、巴罗
• D、阿基米德

第20题：

二项式分布在（）很大，而（）很小，且（）为常数时，二项式分布近似（）分布。

第21题：

第22题：

第23题：