（2）若△P1OA1与△P2A1A2均为等边三角形，求此反比例函数的解析式及A2点的坐标

题目

（2）若△P1OA1与△P2A1A2均为等边三角形，求

此反比例函数的解析式及A2点的坐标

相似考题

1.若反比例函数的图象经过点A(-2,1) ,则它的表达式是 _________________ ．

2.已知过点（0，4），斜率为-1的直线l与抛物线C：y2—2px（b&gt；0）交于A，B两点．（I）求C的顶点到2的距离；（Ⅱ）若线段AB中点的横坐标为6，求C的焦点坐标．

3.正比例函数ｙ＝ｘ的图像与反比例函数y=k/x图像有一个交点的纵坐标是２，求（１）当ｘ＝－３时，反比例函数ｙ的值；（２）当-3<x<-1时反比例函数ｙ的取值范围？

4.（2）求经过A、O、B三点的抛物线的解析式；

更多“(2)若△P1OA1与△P2A1A2均为等边三角形,求 此反比例函数的解析式及A2点的坐标 ”相关问题

  • 第1题：

    根据二次函数图象上三个点的坐标，求出函数解析式：

    （1）（-1，3）（1，3）（2，6）；     

    （2） （-1，-1）（0，-2）（1，1）；

    （3） （-1，0）（3，0）（1，-5）； 

    （4） （1，2）（3，0）（-2，20）。

  • 第2题：

    已知函数f(x)=㏑(x+2)-x2+bx+c，
    (1)若点P(-1，0)在f(x)的图象上，过点P的切线与直线y=-x+2平行，求f(x)的解析式；
    (2)若f(x)在区间[0，2]上单调递增，求b的取值范围。


    答案：
    解析：

  • 第3题：

    若p为某多项式系数向量，x为自变量，则roots（p)的功能是（）。

    A．求多项式在x=0点的函数值

    B．求多项式的导函数

    C．求多项式方程的根

    D．判断多项式是否过零点


    求多项式方程的根

  • 第4题：

    已知一次函数的图象经过点A（2，1），B（－1，－3）

    （1）求此一次函数的解析式；

    （2）求此一次函数的图象与x轴、y轴的交点坐标；

    （3）求此一次函数的图象与两坐标轴所围成的三角形面积。


    正确答案：

    （1）y=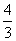x －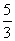    

        (2)与x轴的交点坐标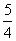（,0）；与y轴的交点坐标(0,－ )

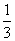        (3)面积为

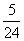
  • 第5题：

    已知二次函数f(x)的二次项系数为实数a，且其图像与直线2x+y=0交点横坐标为1和3．
    (1)若方程f(x)+6a=0有两个相等的实数根，求f(x)的解析式；
    (2)若f(x)的最大值为正数，求实数n的取值范围．


    答案：
    解析：
    解：根据题意f(x)与2x+y=0的交点为(1，-2)、(3，-6)，设f(x)=ax2+bx+c，将上述两个交点代入，有a+b+c=-2，9a+36+c=-6，整理可得b=-2-4a，c=3a.

相关内容