单选题微分方程y″－2y′＝xe2x的特解具有形式（　　）。A y*＝Axe2xB y*＝（Ax＋B）e2xC y*＝x（Ax＋B）e2xD y*＝x2（Ax＋B）e2x

题目
单选题
微分方程y″－2y′＝xe2x的特解具有形式（　　）。
A

y*＝Axe2x

B

y*＝（Ax＋B）e2x

C

y*＝x（Ax＋B）e2x

D

y*＝x2（Ax＋B）e2x

相似考题

1.y"+y=xcos2x的特解的待定形式为( )。A、y=(ax+b)cos2x+(cx+d)sin2x B、acos2x+bsin2x C、y=axcos2x+bxsin2x D、y=asin2x

2.以y1=ex，y2=e-3x为特解的二阶线性常系数齐次微分方程是: A. y''-2y'-3y=0 B. y''+2y'-3y=0 C. y''-3y'+2y=0 D. y''+2y'+y=0

3.方程y"-5y'+6y=xe2x的一个特解为( )。

4.微分方程y''-3y'+2+2y=xex的待定特解的形式是： A. y= (Ax2 +Bx)ex B. y=(Ax+B)ex C. y=Ax2ex D. y=Axex

更多“单选题微分方程y″－2y′＝xe2x的特解具有形式（　　）。A y*＝Axe2xB y*＝（Ax＋B）e2xC y*＝x（Ax＋B）e2xD y*＝x2（Ax＋B）e2x”相关问题

  • 第1题：

    微分方程y"-3y'+2y=xex的待定特解的形式是：

    A. y=（Ax2+Bx）ex
    B. y=（Ax+B）ex
    C. y=Ax2ex
    D. y=Axex

    答案：A
    解析：
    提示：特征方程：r2 -3r + 2 = 0，r1 = 1，r2 = 2 ，f（x）=xex，λ=1，为对应齐次方程的特征方程的单根，
    ∴特解形式y* = x（Ax +B） *ex

  • 第2题：

    微分方程y′′-2y=ex的特解形式应设为（ ）

    A.y*=Aex
    B.y*=Axex
    C.y*=2ex
    D.y*=ex

    答案：A
    解析：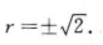
    【考情点拨】本题考查了二阶线性微分方程的特解形式的知识点.【应试指导】由方程知，其特征方程为，r2-2=0，有两个特征根 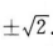.又自由项f(x)=ex，λ=1不是特征根，故特解y*可设为Aex.

  • 第3题：

    下列微分方程是线性微分方程的是（）。

    • A、x（y’）2+y=ex
    • B、xy"+xy’+y=cosx
    • C、y3y"+y’+2y=0
    • D、y"+2y"+y2=0

    正确答案:B

  • 第4题：

    已知y倚x的回归方程为：y＝ax＋b，则可直接导出x倚y的回归方程为：x＝（1/a）y－b/a。


    正确答案:错误

  • 第5题：

    以为特解的二阶线性常系数齐次微分方程是（）。

    • A、y＂-2y＇-3y=0
    • B、y＂+2y＇-3y=0
    • C、y＂-3y＇+2y=0
    • D、y＂-2y＇-3y=0

    正确答案:B

  • 第6题：

    单选题
    微分方程y″－3y′＋2y＝xex的待定特解的形式是（　　）。[2013年真题]
    A

    y＝（Ax2＋Bx）ex

    B

    y＝（Ax＋B）ex

    C

    y＝Ax2ex

    D

    y＝Axex


    正确答案： A
    解析：
    形如y″＋py′＋qy＝P（x）eαx的非齐次方程的特解为：y*＝xkQ（x）eαx，其中k的取值视α在特征方程中的根的情况而定，Q（x）的设法视P（x）的次数而定。在此，特征方程r2－3r＋2＝0的特征根为r＝2，r＝1为单根形式，故k＝1；P（x）＝x，为一次函数，可设Q（x）＝Ax＋B。故原微分方程的待定特解的形式为：x（Ax＋B）ex＝（Ax2＋Bx）ex。

  • 第7题：

    单选题
    微分方程y″-5y′+6y=xe2x的特解形式是：（）
    A

    Ae2x+（Bx+C.

    B

    （Ax+B.e2x

    C

    C.x2（Ax+e2x

    D

    D.x（Ax+e2x


    正确答案： A
    解析： 暂无解析

  • 第8题：

    单选题
    以y1＝ex，y2＝e－3x为特解的二阶线性常系数齐次微分方程是（　　）。[2012年真题]
    A

    y″－2y′－3y＝0

    B

    y″＋2y′－3y＝0

    C

    y″－3y′＋2y＝0

    D

    y″－2y′－3y＝0


    正确答案： B
    解析：
    因y1＝ex，y2＝e－3x是特解，故r1＝1，r2＝－3是特征方程的根，因而特征方程r2＋2r－3＝0。故二阶线性常系数齐次微分方程是：y″＋2y′－3y＝0。

  • 第9题：

    问答题
    设二阶线性微分方程y″＋P（x）y′＋Q（x）y＝f（x）的三个特解是y1＝x，y2＝ex，y3＝e2x，试求此方程满足条件y（0）＝1，y′（0）＝3的特解。

    正确答案：
    由题意可知,Y1=ex-x、Y2=e2x-x是原方程对应齐次方程的两个线性无关的解[因(ex-x)/(e2x-x)≠常数],故原方程的通解为y=C1(ex-x)+C2(e2x-x)+x,由y(0)=1,y′(0)=3,得C1=-1,C2=2。故所求原方程的特解为y=-(ex-x)+2(e2x-x)+x=2e2x-ex。
    解析： 暂无解析

  • 第10题：

    单选题
    具有待定特解形式为y=A1x+A2+B1ex的微分方程是下列中哪个方程（）？
    A

    y″+y′-2y=2+ex

    B

    y″-y′-2y=4x+2ex

    C

    y″-2y′+y=x+ex

    D

    y″-2y′=4+2ex


    正确答案： C
    解析： 暂无解析

  • 第11题：

    对于微分方程y"-2y'+y=xex，利用待定系数法求其特解y*时，下列特解设法正确的是（）

    A.Y*=(Ax+B)ex
    B.y*=x(Ax+B)ex
    C.y*=Ax3ex
    D.Y*=x2(Ax+B)ex

    答案：D
    解析：

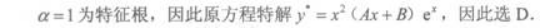
  • 第12题：

    具有待定特解形式为y=A1x+A2+B1ex的微分方程是下列中哪个方程（）？

    • A、y″+y′-2y=2+ex
    • B、y″-y′-2y=4x+2ex
    • C、y″-2y′+y=x+ex
    • D、y″-2y′=4+2ex

    正确答案:B

  • 第13题：

    在y=ax+b中，（）是直线的斜率。

    • A、y
    • B、a
    • C、x
    • D、b

    正确答案:B

  • 第14题：

    设随机变量X~N（0，1），Y=aX+b（a＞0），则（）

    • A、Y~N（0，1）
    • B、Y~N（b，a）
    • C、Y~N（b，a2）
    • D、Y~N（a+b，a2）

    正确答案:C

  • 第15题：

    下列结论不正确的是（）。

    • A、y"+y=ex的一个特解的待定形式为y*=Aex
    • B、y"+y=sinx的一个特解的待定形式为y*=x（c1cosx+c2sinx）
    • C、y"-4y’+4y=e2x的一个特解的待定形式为y*=Axe2x
    • D、D.y"-4y’+4y=x2的一个特解的待定形式为y*-（Ax2+Bx+x

    正确答案:D

  • 第16题：

    单选题
    以为特解的二阶线性常系数齐次微分方程是（）。
    A

    y＂-2y＇-3y=0

    B

    y＂+2y＇-3y=0

    C

    y＂-3y＇+2y=0

    D

    y＂-2y＇-3y=0


    正确答案： C
    解析： 暂无解析

  • 第17题：

    单选题
    要使E[Y－（aX＋b）]2达到最小，则常数a＝（　　）。b＝（　　）。
    A

    a＝Cov（X，Y）/D（X）；b＝E（Y）－[E（X）Cov（X，Y）/D（X）D（Y）]

    B

    a＝Cov（X，Y）/D（X）；b＝E（Y）－[E（X）Cov（X，Y）/D（X）]

    C

    a＝Cov（X，Y）；b＝E（Y）－[E（X）Cov（X，Y）/D（X）]

    D

    a＝Cov（X，Y）；b＝E（Y）－[E（X）Cov（X，Y）/D（X）D（Y）]


    正确答案： C
    解析：
    E[Y－（aX＋b）]2＝E[Y2－2aXY－2bY＋a2X2＋2abX＋b2]＝E（Y2）－2aE（XY）－2bE（Y）＋a2E（X2）＋2abE（X）＋b2
    记上式为f，则f为a，b的多元函数，根据多元函数求极值的方法，则令
    fa′＝－2E（XY）＋2aE（X2）＋2bE（X）＝0
    fb′＝－2E（Y）＋2aE（X）＋2b＝0
    解得
    a＝[E（XY）－E（X）E（Y）]/D（X）＝Cov（X，Y）/D（X）
    b＝E（Y）－aE（X）＝E（Y）－E（X）Cov（X，Y）/D（X）

  • 第18题：

    单选题
    （2012）以y1=ex，y2=e-3x为特解的二阶线性常系数齐次微分方程是：（）
    A

    y″-2y′-3y=0

    B

    y″+2y′-3y=0

    C

    y″-3y′+2y=0

    D

    y″+2y′+y=0


    正确答案： D
    解析： 暂无解析

  • 第19题：

    单选题
    下列结论不正确的是（）。
    A

    y+y=ex的一个特解的待定形式为y*=Aex

    B

    y+y=sinx的一个特解的待定形式为y*=x（c1cosx+c2sinx）

    C

    y-4y’+4y=e2x的一个特解的待定形式为y*=Axe2x

    D

    D.y-4y’+4y=x2的一个特解的待定形式为y*-（Ax2+Bx+x


    正确答案： A
    解析： y"+y=0的特征根为λ=±i，故（A）、（B）的特解的形式均正确，y"-4y’+4y=0的特征方程为λ2-4λ+4=0，（λ-2）2=0，有一个二重根λ1,2=2，故（C）的特解的形式正确，而（D）不正确。

相关内容