2、如果一个5×4矩阵A的秩为3，则它的列向量组的秩为4.

题目

2、如果一个5×4矩阵A的秩为3，则它的列向量组的秩为4.

相似考题

1.设三阶实对称矩阵的特征值为3,3,0,则A的秩r(A)=()A、2B、3C、4D、5

2.对于有5个变量的齐次线性方程组AX=0,系数矩阵的秩r(A)=3,则其基础解析中向量个数为()。A.2B.5C.3D.1

3.设A为m×n矩阵，C是n阶可逆矩阵，矩阵A的秩为r1，矩阵B=AC的秩为r，则

4.向量组α1=（1，0，0），α2=（1，1，0），α3=（1，1，1）的秩为（ ）A.1 B.2C.3 D.4

更多“2、如果一个5×4矩阵A的秩为3，则它的列向量组的秩为4.”相关问题

  • 第1题：

    设矩阵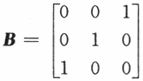，已知矩阵A相似于B，则秩(A-2E)与秩(A-E)之和等于

    A.2
    B.3
    C.4
    D.5

    答案：C
    解析：

  • 第2题：

    下列结论中正确的是（　　）。

    A、 矩阵A的行秩与列秩可以不等
    B、 秩为r的矩阵中，所有r阶子式均不为零
    C、 若n阶方阵A的秩小于n，则该矩阵A的行列式必等于零
    D、 秩为r的矩阵中，不存在等于零的r-1阶子式

    答案：C
    解析：
    A项，矩阵A的行秩与列秩一定相等。B项，由矩阵秩的定义可知，若矩阵A（m×n）中至少有一个r阶子式不等于零，且r＜min（m，n）时，A中所有的r+1阶子式全为零，则A的秩为r。即秩为r的矩阵中，至少有一个r阶子式不等于零，不必满足所有r阶子式均不为零。C项，矩阵A的行列式不等于零意味着矩阵A不满秩，n阶矩阵的秩为n时，所对应的行列式的值大于零；当n阶矩阵的秩＜n时，所对应的行列式的值等于零。D项，秩为r的矩阵中，有可能存在等于零的r-1阶子式，如秩为2的矩阵



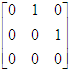
    中存在等于0的1阶子式。

  • 第3题：

    设向量组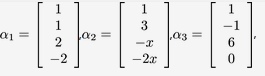,，若此向量组的秩为2，求的值。


    答案：
    解析：

  • 第4题：

    设矩阵，α1，α2，α3为线性无关的3维列向量组，则向量组Aα1，Aα2，Aα3的秩为_________.


    答案：1、2.
    解析：
    因(Aα1，Aα2，Aα3)=A(α1，α2，α3)，又α，α，α是三维线性无关列向量，所以(α1，α2，α3)为三阶可逆矩阵故r(Aα1，Aα2，Aα3)=r(A)=2.

  • 第5题：

    设α为三维单位列向量，E为三阶单位矩阵，则矩阵E-αα^T的秩为________.


    答案：
    解析：

  • 第6题：

    设A为3阶实对称矩阵，A的秩为2，且.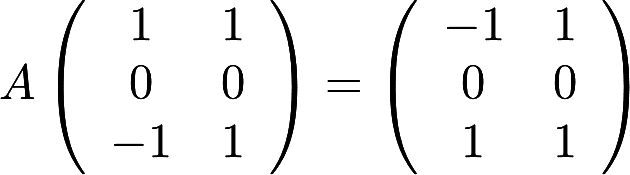 （Ⅰ）求A的特征值与特征向量； （Ⅱ）求矩阵A


    答案：
    解析：

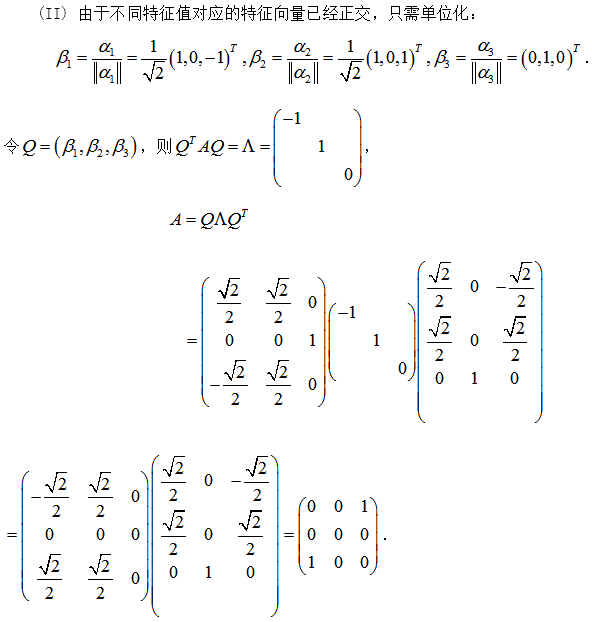
  • 第7题：

    设A是5×6矩阵，则（ ）正确。
    A.若A中所有5阶子式均为0,则秩R(A)=4
    B.若秩R(A)=4,则A中5阶子式均为0
    C.若秩R(A)=4，则A中4阶子式均不为0
    D.若A中存在不为0的4阶子式，则秩R(A)=4


    答案：B
    解析：
    提示：利用矩阵秩的定义。

  • 第8题：

    设有向量组α1=（2，1，4，3）T，α1=（-1，1，-6，6）T，α3=（-1，-2，2，-9）T，α4=（1，1，-2，7）T，α5=（2，4，4，9）T，则向量组α1，α2，α3，α4，α5的秩是（）。

    • A、1
    • B、2
    • C、3
    • D、4

    正确答案:C

  • 第9题：

    单选题
    设向量组Ⅰ：α(→)1，α(→)2，…，α(→)m，其秩为r；向量组Ⅱ：α(→)1，α(→)2，…， α(→)m，β(→)，其秩为s，则r＝s是向量组Ⅰ与向量组Ⅱ等价的（　　）。
    A

    充分非必要条件

    B

    必要非充分条件

    C

    充分必要条件

    D

    既非充分也非必要条件


    正确答案： A
    解析：
    两向量组等价的充要条件是它们有相同的秩。

  • 第10题：

    问答题
    设向量组α1，α2，…，α5的秩为r＞0，证明:（1）α1，α2，…，α5中任意r个线性无关的向量都构成它的一个极大线性无关组；（2）若α1，α2，…，α5中每个向量都可由其中某r个向量线性表示，则这r个向量必为α1，α2，…，α5的一个极大线性无关组。

    正确答案：
    (1)设①:αj1,αj2,…,αjr是α1,α2,…,αs中任意r个线性无关的向量,由于向量组的秩为r,故向量组中任意多余r个向量的向量组必线性相关,所以
    αj1,αj2,…,αjr,αi(i=1,2,…,s;i≠j1,j2,…,jr)
    线性相关,从而①为原向量组的极大线性无关组.
    (2)设①:αj1,αj2,…,αjr是α1,α2,…,αs中的r个向量,且原向量组中每个向量都可由①线性表示,则原向量组与向量组①等价.等价向量组有相同的秩,原向量组的秩为r,所以向量组①的秩为r.又向量组①只含r个向量,故向量组①线性无关,因此①是原向量组的极大线性无关组.
    解析： 暂无解析

  • 第11题：

    单选题
    设向量组（I）α1，α2，…，αs，其秩为r1，向量组（Ⅱ）β1，β2，…，βs，其秩为r2，且βi（i=1，2，…，s）均可以由α1，…，αs线性表示，则（　　）.
    A

    向量组α1+β1，α2+β2，…，αs+βs的秩为r1+r2

    B

    向量组α1-β1，α2-β2，…，αs-βs秩为rl-r2

    C

    向量组α1，α2，…，αs，β1，β2，…，βs的秩为rl+r2

    D

    向量组α1，α2，…，αs，β1，β2，…，βs的秩为rl


    正确答案： A
    解析：
    向量组β1，β2，…，βs可由向量组α1，α2，…，αs线性表示，则向量组α1，α2，…，αs，β1，β2，…，βs也可由其线性表示，所以α1，α2，…，αs向量组的极大线性无关组也是该向量组的极大线性无关组，故其秩为rl．

  • 第12题：

    单选题
    设α(→)1，α(→)2，…，α(→)s和β(→)1，β(→)2，…，β(→)t为两个n维向量组，且秩（α(→)1，α(→)2，…，α(→)s）＝秩（β(→)1，β(→)2，…，β(→)t）＝r，则（　　）。
    A

    此两个向量组等价

    B

    秩（α(→)1，α(→)2，…，α(→)s，β(→)1，β(→)2，…，β(→)t）＝r

    C

    当α(→)1，α(→)2，…，α(→)s可以由β(→)1，β(→)2，…，β(→)t线性表示时，此二向量组等价

    D

    s＝t时，二向量组等价


    正确答案： C
    解析：
    两向量组等价的充要条件是所含向量的个数相等，且能相互线性表示。

  • 第13题：

    向量组的秩等于( )。

    A、1
    B、2
    C、3
    D、4

    答案：B
    解析：
    向量组对应的矩阵为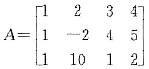，对A进行初等行变换 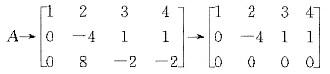可见R(A)=2，从而向量组的秩为2

  • 第14题：

    设矩阵，则A^3的秩为________


    答案：
    解析：

  • 第15题：

    设A为m×n矩阵，B为n×m矩阵，E为m阶单位矩阵，若AB=E，则



    A.A秩r(A)=m，秩r(B)=m
    B.秩r(A)=m，秩r(B)=n
    C.秩r(A)=n，秩r(B)=m
    D.秩r(A)=n，秩r(B)=n

    答案：A
    解析：
    本题考的是矩阵秩的概念和公式.因为AB=E是m阶单位矩阵，知r(AB)=m.又因r(AB)≤min(r(A)，r(B))，故m≤r(A)，m≤r(B). ①另一方面，A是m×n矩阵，B是n×m矩阵，又有r(A)≤m，r(B)≤m. ②比较①、②得r(A)=m，r(B)=m.所以选(A)

  • 第16题：

    设α，β为三维列向量，矩阵A=αα^T+ββ^T，其中α^T，β^T分别是α，β的转置.证明：
    　　(Ⅰ)秩r(A)≤2；
    　　(Ⅱ)若α，β线性相关，则秩r(A)<2.


    答案：
    解析：
    【证明】(Ⅰ)因为α，β为三维列向量，那么αα^T和ββ^T都是三阶矩阵，
    且秩r(αα^T)≤1，r(ββ^T)≤1.
    那么，r(A)=r(αα^T+ββ^T)≤r(αα^T)+r(ββ^T)≤2.
    (Ⅱ)由于α，β线性相关，不妨设α=kβ，于是
    r(A)=r(αα^T+ββ^T)=r((1+k^2)ββ^T)≤r(β)≤1<2.
    【评注】本题考查矩阵秩的性质公式.
    (Ⅰ)中有两个基本知识点：①r(αα^T)≤1和②r(A+B)≤r(A)+r(B).
    (Ⅱ)中有两个基本知识点：①α，β线性相关的几何意义和②r(kA)=r(A)，k≠0.
    注意，如果分块矩阵比较熟悉，本题的(Ⅰ)也可如下处理：
    因为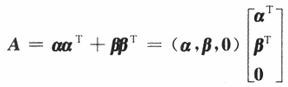

    那么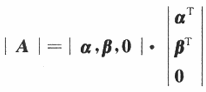
    从而r(A)≤2.

  • 第17题：

    设A为三阶实对称矩阵，A的秩为2，且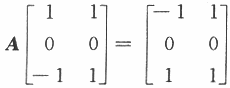

    　　(Ⅰ)求A的所有特征值与特征向量；
    　　(Ⅱ)求矩阵A.


    答案：
    解析：

  • 第18题：

    4阶方阵A的秩为2，则其伴随矩阵An的秩为（ ）。

    A. 0 B. 1 C. 2 D. 3


    答案：A
    解析：
    提示：A所有三阶子式为零，故An是零矩阵。

  • 第19题：

    设A、B分别为n×m，n×l矩阵，C为以A、B为子块的n×（m+l）矩阵，即C=（A，B），则（ ）.《》（ ）

    A.秩（C）=秩（A）
    B.秩（C）=秩（B）
    C.秩（C）与秩（A）或秩（C）与秩（B）不一定相等
    D.若秩（A）=秩（B）=r，则秩（C）=r

    答案：C
    解析：

  • 第20题：

    单选题
    设A为4×5矩阵，且A的行向量组线性无关，则（　　）。
    A

    A的列向量组线性无关

    B

    方程组AX(→)＝b(→)有无穷多解

    C

    方程组AX(→)＝b(→)的增广矩阵A(＿)的任意四个列向量构成的向量组线性无关

    D

    A的任意4个列向量构成的向量组线性无关


    正确答案： B
    解析：
    方程组AX(→)＝b(→)的行向量组线性无关，则r（A）＝4，而未知数的个数为5，故方程组中含有一个自由未知数，它有无穷多解。

  • 第21题：

    单选题
    设向量组I：α(→)1，α(→)2，…，α(→)m，其秩为r；向量组II：α(→)1，α(→)2，…，α(→)m，β(→)，其秩为s，则r＝s是向量组I与向量组II等价的（　　）。
    A

    充分非必要条件

    B

    必要非充分条件

    C

    充分必要条件

    D

    既非充分也非必要条件


    正确答案： C
    解析：
    两向量组等价的充要条件是它们有相同的秩。

  • 第22题：

    问答题
    设向量组α(→)1，α(→)2，…，α(→)s的秩为r＞0，证明：　　（1）α(→)1，α(→)2，…，α(→)s中任意r个线性无关的向量都构成它的一个极大线性无关组；　　（2）若α(→)1，α(→)2，…，α(→)s中每个向量都可由其中某r个向量线性表示，则这r个向量必为α(→)1，α(→)2，…，α(→)s的一个极大线性无关组。

    正确答案：
    (1)设①:α(→)j1,α(→)j2,…,α(→)jr是α(→)1,α(→)2,…,α(→)s中任意r个线性无关的向量,由于向量组的秩为r,故向量组中任意多于r个向量的向量组必线性相关,所以α(→)j1,α(→)j2,…,α(→)jr,α(→)i(i=1,2,…,s;i≠j1,j2,…,jr)线性相关,从而①为原向量组的极大线性无关组。
    (2)设①:α(→)j1,α(→)j2,…,α(→)jr是α(→)1,α(→)2,…,α(→)s中的r个向量,且原向量组中每个向量都可由①线性表示,则原向量组与向量组①等价。等价向量组有相同的秩,原向量组的秩为r,所以向量组①的秩为r。又向量组①只含r个向量,故向量组①线性无关,因此由(1)的结论有①是原向量组的极大线性无关组。
    解析： 暂无解析

  • 第23题：

    单选题
    n元线性方程组AX(→)＝b(→)有唯一解的充要条件为（　　）。
    A

    A为方阵且｜A｜≠0

    B

    导出组AX(→)＝0(→)仅有零解

    C

    秩（A）＝n

    D

    系数矩阵A的列向量组线性无关，且常数向量b(→)与A的列向量组线性相关


    正确答案： C
    解析：
    A项，系数矩阵A不一定是方阵；B项，导出组只有零解，方程组AX(→)＝b(→)不一定有解；C项，当r（A）＝n时，不一定有r（A）＝r（A(＿)）＝n；D项，b(→)可由A的列向量组线性表示，则方程组AX(→)＝b(→)有唯一解。

  • 第24题：

    单选题
    下列结论中正确的是（    ）
    A

    矩阵A的行秩与列秩可以不等

    B

    秩为r的矩阵中，所有r阶子式均不为零

    C

    若n阶方阵A的秩小于n，则该矩阵A的行列式必等于零

    D

    秩为r的矩阵中，不存在等于零的r-1阶子式


    正确答案： D
    解析：

相关内容