名同志站成一排: (1)其中某甲必须站在排头,有多少种站法 (2)其中某甲不站在排头,有多少种站法 (3)其中某甲不站在排头,也不站在排尾,有多少种站法
题目
(1)其中某甲必须站在排头,有多少种站法
(2)其中某甲不站在排头,有多少种站法
(3)其中某甲不站在排头,也不站在排尾,有多少种站法
相似考题
更多“名同志站成一排: ”相关问题
-
第1题:
3名学生和2名老师站成一排照相,2名老师必须站在一起且不在边上的不同排法共有:
A. 12种 B. 24种 C. 36种 D. 48种
正确答案:B2名老师可以站在2,3位或者3,4位。每一种的不同排法是3!×2=12。则总共有12×2=24种排法。
-
第2题:
某单位有78个人,站成一排,从左边向右数,小王是第50个,从右边向左数,小张是第48个,则小王和小张之间有多少个人?
A.16
B.17
C.18
D.20
正确答案:C
C【解析】从左向右数,小王是第50个,则从右向左数,小王是第29个,因为从右向左数,小张是第48个,所以小王与小张之间有48-29-1=18个人。
-
第3题:
4男2女6个人站成一排合影留念,要求2个女的紧挨着排在正中间,有( )种不同的排法。
A.26
B.36
C.60
D.48
正确答案:D
先排男的,有4×3×2×1=24(种),再排女的,有2种,共有24×2=48(种)。故选D。 -
第4题:
身高不等的7人站成一排照相,要求身高最高的人排在中间,按身高向两侧递减。共有多少种排法?A.20
B.24
C.36
D.48答案:A解析:因为7人身高不等,且按身高向两侧递减,因此除去中间最高的人,只需要从6人中选出3人排在一边即可。此时,这3人的排法根据他们的身高已经确定。同理,剩下的3人的排法也已经确定。因此一共有C63=20种排法。 -
第5题:
某班有78个人,站成一排,从左向右数,小赵是第50个,从右向左数,小李是第48个, 则小赵小李之间有多少人?( )A. 16
B. 17
C. 18
D. 20答案:C解析:由题意,从左向右数,小赵是第50个,则从右向左数,小赵是第29个,故小赵、小李之间有48—29=18人。 -
第6题:
6名学生和l名教师站成一排照相,教师必须站在中间的站法有( )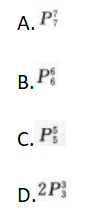 答案:B解析:【考情点拨】本题主要考查的知识点为排列数. 【应试指导】此题是有条件限制的排列问题.让教师站在中间,6名学生的全排列有
答案:B解析:【考情点拨】本题主要考查的知识点为排列数. 【应试指导】此题是有条件限制的排列问题.让教师站在中间,6名学生的全排列有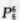 种.
种. -
第7题:
对队列队形练习的基本术语描述正确的是( )。A.学生左右并列站成一排叫路
B.学生前后重叠站成一行叫列
C.队形的两端叫翼
D.每排第一个学生叫基准学生答案:C解析:本题考查的是队列队形练习的基本术语的知识点。
C项,队形的两端叫翼。左端为左翼,右端为右翼。综上,C正确。
A项,学生左右并列站成一排叫列。故排除。
B项,学生前后重叠站成一行叫路。故排除。
D项,按照规定队形列队时,站在排头或者教师指定的学生,作为看齐或行动的目标叫基准学生。故排除。
故正确答案为C。
-
第8题:
若6位同学站成一排,其中甲、乙两位同学相邻站立,则不同的站法有( )种。A.120
B.240
C.360
D.720答案:B解析:甲乙捆绑后再排序,
-
第9题:
运统1中的编组站名,应填记()。
- A、编组站名
- B、列车始发站名
- C、区段站名
- D、装车站名
正确答案:B -
第10题:
若干名文艺战士进行舞蹈彩排,一会儿站成(前后、左右对正)实心正方形,一会儿又站成(插缝)实心正三角形。站成正三角形时比站成正方形每边多两个人。则彩排的战士人数是()
- A、49
- B、34
- C、36
- D、38
正确答案:C -
第11题:
填空题按 请 从高到低的 顺序 一排 站成____正确答案: 请按从高到低的顺序站成一排。解析: 暂无解析 -
第12题:
单选题运统l中的编组站名,应填记()。A编组站名
B列车始发站名
C区段站名
D装车站名
正确答案: D解析: 暂无解析 -
第13题:
训练时,若干名新兵站成一排,从一开始报数,除了甲以外其他人报的数之和减去甲报的数恰好等于50,共有多少名新兵?
A.10
B.11
C.12
D.13
正确答案:B
【答案】B
【解析】采用代入法,所有人数所报数字之和减去50等于甲所报数字的二倍,可排除A。假设当人数为11时,所报数字之和为1+2+……+11=66,=8<11,符合题意,此时共有11名新兵。
-
第14题:
3名学生和2名老师站成一排照相,2名老师必须相邻且都不在边上的不同排法共有 ( )种。
A.12
B.24
C.36
D.48
正确答案:B
[答案] B。解析:2名老师可以是在2,3位或者3,4位。每一种的不同排法是3!×2=12。则总共有12×2=24种排法。
-
第15题:
3位男生和3位女生共6位同学站成一排,若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数是
A. 360 B. 228 C. 216 D. 96
正确答案:B
-
第16题:
四名学生和两位老师站一排照相,两老师不在两头但相邻的排法有()种。[2010年湖北省农村信用社真题]
A.72
B.108
C.144
D.288答案:C解析:方法一:
第一步,把两个老师看成一个整体,即一个人,这样相当于只有5个人排队。由于老师不能排在两端,所以应该从中间的三个位置中选一个位置给老师排,而两个老师之间可以互换.所以这样两个老师共有种不同的排法;第二步:排学生,剩余四个位置四个学生排,共有
种排法。所以一共有6×
=144种不同的排法。
方法二:用间接法
老师相邻的全部排法有:;老师排在两端的排法有:4×
=96;所以,一共有240—96=144种不同的排法。
-
第17题:
训练时,若干名新兵站成一排,从一开始报数,除了甲以外其他人报的数之和减去甲报的数恰好等于50,共有多少名新兵?A. 10
B. 11
C. 12
D. 13答案:B解析:
-
第18题:
3位女生和2位男生站成一排,若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数是( )A.24
B.36
C.48
D.60
E.72答案:C解析:
-
第19题:
某班有50名学生,上体育课的时候面向老师站成一排报数,老师先让报数是4的倍数的向后转,再让报数是5的倍数的向后转,接着又让是6的倍数的向后转,最终面向老师的学生有( )名?
A. 30
B. 34
C. 38
D. 42答案:B解析:本题考查容斥原理。报数是4的倍数的有12人,5的倍数的有10人,6的倍数的有8人,转过2次的有4+2+1=7人,转过3次的0人。则转过的人共有12+10+8-7=23人,则没有转过的人为27人。转过2次的人也是面向老师的,所以最终面向老师的学生有27+7=34人。因此,本题答案为B选项。 -
第20题:
小修时进入密封容器,腰部要系好安全带,并设()监护。
- A、两名男同志
- B、两名女同志
- C、一名男同志
- D、一名女同志
正确答案:A -
第21题:
甲、乙、丙、丁三人站成一排,甲必须站在排头,一共有()种排法。
- A、6
- B、8
- C、4
正确答案:A -
第22题:
单选题甲、乙、丙、丁三人站成一排,甲必须站在排头,一共有()种排法。A6
B8
C4
正确答案: A解析: 暂无解析 -
第23题:
单选题训练时,若干名新兵站成一排,从“一”开始报数,除了甲以外其他人报的数之和减去甲报的数恰好等于50。共有多少名新兵?( )A10
B11
C12
D13
正确答案: D解析:
由题意可知,所有人报的数这和减去50应为甲报的数字的2倍。A项错误,从1到10的和为55,减去50为奇数。当人数为11时,所报数字之和为1+2+…+11=66,(66-50)÷2=8<11,符合要求,即共有11名新兵。
