随机变量Y的概率分布表如下：随机变量Y的方差为( )。A．76B．16C．6D．68

题目

随机变量Y的概率分布表如下：

随机变量Y的方差为( )。

A．76

B．16

C．6

D．68

相似考题

1.随机变量Y的概率分布表如下： Y 1 4 P 60% 40%随机变量y的方差为（ ）。A．2.66B．2.16C．4.26D．4.58

2.随机变量Y的概率分布表如下：A．2.66B．2.16C．4.26D．4.58

3.设随机变量X与Y独立，其中X的概率分布为而Y的概率密度为f(y)，求随机变量U=X+Y的概率密度g(u).

4.随机变量Y的概率分布表如下：随机变量Y的方差为( )。A．2.76B．2.16C．4.06D．4.68

更多“ 随机变量Y的概率分布表如下：随机变量Y的方差为( )。A．76B．16C．6D．68 ”相关问题

  • 第1题：

    设随机变量X的概率密度为令随机变量，
    　　(Ⅰ)求Y的分布函数；
    　　(Ⅱ)求概率P{X≤Y}.


    答案：
    解析：
    【分析】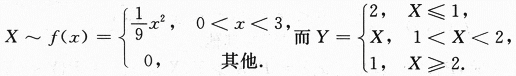
    Y是随机变量X的函数，只是这函数是分段表示的，这样得到的Y可能是非连续型，也非离散型，
    【解】(Ⅰ)设Y的分布函数为FYy)，显然P{1≤Y≤2}=1，所以，
    当y<1时，FY(y)=P{Y≤y)=0；
    当1≤y<2时，FY(y)=P{Y≤y}=P{Y<1}+P{Y=1}+P{1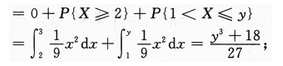
    当2≤y时，FY(y)=P{Y≤y}=P{Y≤2}=1.
    总之，Y的分布函数为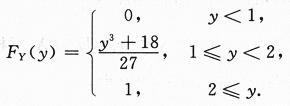

    (Ⅱ)因为Y=

  • 第2题：

    某些资产的预期收益率y的概率分布如表1—4所示，则其方差为（　　）。
    表1—4随机变量y的概率分布

    A.2．16
    B.2．76
    C.3．16
    D.4．76

    答案：A
    解析：
    该资产的预期收益率Y的期望为：E(Y)=1×60％+4×40％=2．2；其方差为：Vαr(Y)=0．6×(1-2．2)2+0．4×(4-2．2)2=2．16。

  • 第3题：

    某些资产的预期收益率Y的概率分布如表1—4所示，则其方差为（）。
    表1—4随机变量Y的概率分布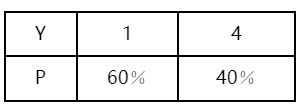

    A.2.16
    B.2．76
    C.3．16
    D.4．76

    答案：A
    解析：
    该资产的预期收益率Y的期望为：E(Y)=1×60％+4×40％=2．2；其方差为：Vαr(Y)=0．6×(1-2．2)2+0．4×(4-2．2)2=2.16。

  • 第4题：

    某些资产的预期收益率y的概率分布如表1—4所示，则其方差为（ ）。
    表1—4随机变量y的概率分布




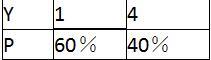
    A.2.16
    B.2．76
    C.3．16
    D.4．76

    答案：A
    解析：
    该资产的预期收益率Y的期望为：E(Y)=1×60％+4×40％=2．2；其方差为：Vαr(Y)=0．6×(1-2．2)2+0．4×(4-2．2)2=2.16。

  • 第5题：

    某些资产的预期收益率y的概率分布如表1—4所示，则其方差为（　　）。?
    表1—4随机变量y的概率分布


    A.2．16
    B.2．76
    C.3．16
    D.4．76

    答案：A
    解析：
    该资产的预期收益率Y的期望为：E(Y)=1×60％+4×40％=2．2；其方差为：Vαr(Y)=0．6×(1-2．2)2+0．4×(4-2．2)2=2．16。

相关内容