均质细杆重力为P、长2L,A端铰支,B端用绳系住,处于水平位置,如图所示。当B端绳突然剪断瞬时,AB杆的角加速度大小为:
题目
均质细杆重力为P、长2L,A端铰支,B端用绳系住,处于水平位置,如图所示。当B端绳突然剪断瞬时,AB杆的角加速度大小为:




相似考题
更多“均质细杆重力为P、长2L,A端铰支,B端用绳系住,处于水平位置,如图所示。当B端绳突然剪断瞬时,AB杆的角加速度大小为: ”相关问题
-
第1题:
图示水平梁AB由铰A与杆支撑。在梁上O处用小轴安装滑轮。轮上跨过软绳。绳一端水平地系于墙上,另端悬持重W的物块。构件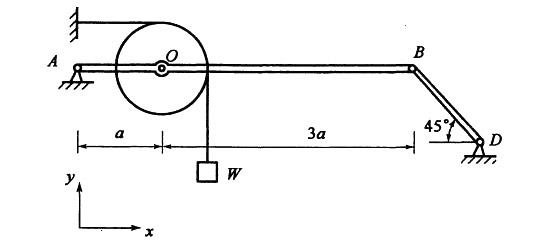 均不计重。铰A的约束力大小为
均不计重。铰A的约束力大小为
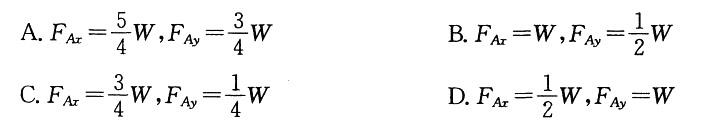 答案:A解析:
答案:A解析:
-
第2题:
杆OA绕固定轴O转动,长为l。某瞬时杆端A点的加速度a如图所示,则该瞬时OA的角速度及角加速度为( )。

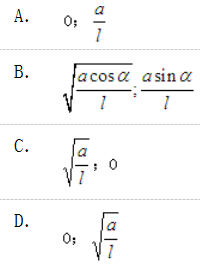 答案:B解析:
答案:B解析:
-
第3题:
杆OA = l,绕固定轴O转动,某瞬时杆端A点的加速度a如图所示,则该瞬时杆OA的角速度及角加速度为:
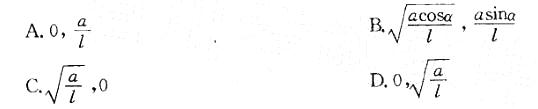 答案:B解析:提示:根据定轴转动刚体上一点加速度与转动角速度、角加速度的关系:an=ω2l,at=αl ,而题中an=acosα , at=asinα。
答案:B解析:提示:根据定轴转动刚体上一点加速度与转动角速度、角加速度的关系:an=ω2l,at=αl ,而题中an=acosα , at=asinα。 -
第4题:
物重力的大小为Q,用细绳BA、CA悬挂(如图所示),α=60°,若将BA绳剪断,则该瞬时CA绳的张力大小为: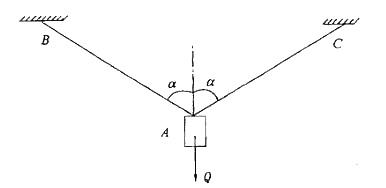 A. 0
A. 0
B. 0.5Q
C.Q
D. 2Q答案:B解析:提示:可用动静法,在A上加惯性力。 -
第5题:
均质细杆AB重力为P,长为2l,A端铰支,B端用绳系住,处于水平位置,如图所示。当B端绳突然剪断瞬时,AB杆的角加速度大小为3g/4l,则A处约束力大小为: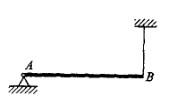
A. FAx= 0,FAy=0 B. FAx= 0,FAy=P/4 C. FAx= P,FAy=P/2 D.FAx= 0,FAy=P答案:B解析:
-
第6题:
均质细杆重P,长2L,A端铰支,B端用绳系住,处于水平位置,如图所示。当B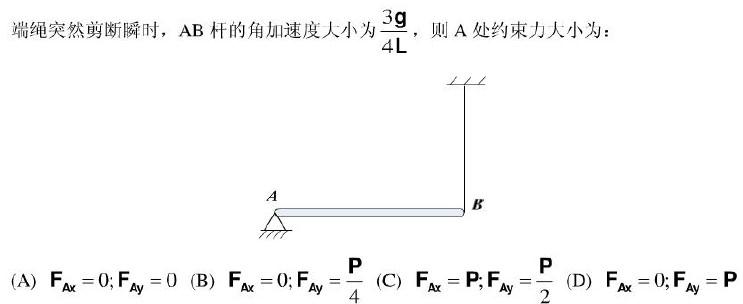 答案:B解析:
答案:B解析: -
第7题:
水平梁AB由铰A与杆BD支撑,在梁上O处用小轴安装滑轮。轮上跨过软绳,绳一端水平系与墙上,另端悬挂重W的物块,构件均不计重,铰A的约束力大小为: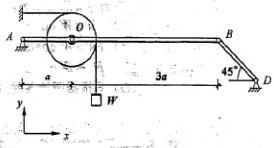
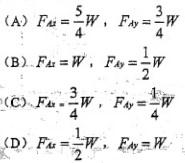 答案:A解析:
答案:A解析: -
第8题:
均质细直杆OA长为l ,质量为m,A端固结一质置为m的小球(不计尺寸),如图所示。当OA杆以匀角速度w绕O轴转动时,该系统时O轴的动量矩为: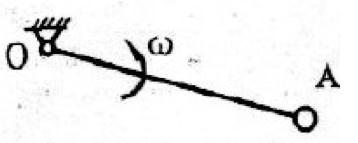
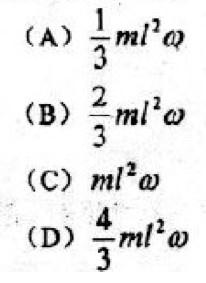 答案:D解析:
答案:D解析:
-
第9题:
均质细直杆长为l,质量为m,图示瞬时点A处的速度为v,则杆AB的动量大小为: 答案:D解析:提示 动量的大小等于杆AB的质量乘以其质心速度的大小。
答案:D解析:提示 动量的大小等于杆AB的质量乘以其质心速度的大小。 -
第10题:
质量为m,长为2l的均质细杆初始位于水平位置,如图4-68所示。A端脱落后, 杆绕轴B转动,当杆转到铅垂位置时,AB杆B处的约束力大小为( )。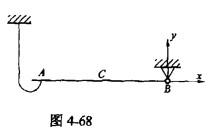
 答案:D解析:提示:根据动能定理,当杆转动到铅垂位置时,杆的ω2=3g/2l,α=0,根据质心运动定理mlω2=FBy-mg,FBx=0。
答案:D解析:提示:根据动能定理,当杆转动到铅垂位置时,杆的ω2=3g/2l,α=0,根据质心运动定理mlω2=FBy-mg,FBx=0。 -
第11题:
均质细杆AB重力为W,A端置于光滑水平面上,B端用绳悬挂如图4-56所示。当绳断后杆在倒地的过程中,质心C的运动轨迹为()。
- A、圆弧线
- B、曲线
- C、铅垂直线
- D、抛物线
正确答案:C -
第12题:
均质细杆AB重力为P、长2L,A端铰支,B端用绳系住,处于水平位置,如图所示,当B端绳突然剪断瞬时,AB杆的角加速度大小为:
 答案:B解析:
答案:B解析:
-
第13题:
如图所示,结构由AB、BC、CE三杆铰接而成,A处为固定端,杆重不计,铰C上作用一铅垂力P,则二力杆为( )。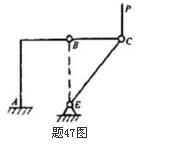 A.AB、BC、CE
A.AB、BC、CE
B.BC、CE
C.AB
D.均不是二力杆答案:B解析:在铅垂力P的作用下,此结构处于平衡状态。由二力平衡原理,不计自重的刚体在二力作用下平衡的必要充分条件是:二力沿着同一作用线、大小相等、方向相反。仅受两个力作用且处于平衡状态的物体,称为二力体,又称二力杆件,故杆BC和杆CE是二力杆。 -
第14题:
图示均质细直杆AB长为l,质量为m,图示瞬时A点的速度为则AB杆的动量大小为: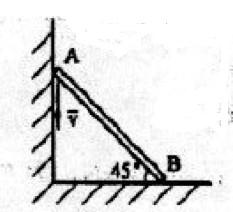
 答案:D解析:质点系动量:
答案:D解析:质点系动量: ,为各质点动量的矢量和,图示杆的质心在杆中端。
,为各质点动量的矢量和,图示杆的质心在杆中端。 -
第15题:
杆OA绕固定轴0转动,长为l。某瞬时杆端A点的加速度a如图所示,则该瞬时OA 的角速度及角加速度为: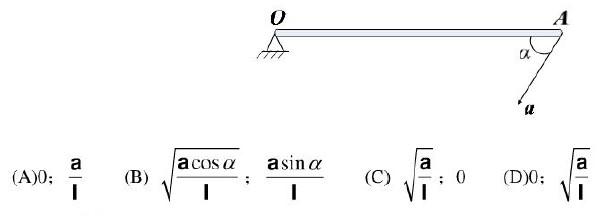 答案:C解析:解:选C
答案:C解析:解:选C
-
第16题:
均质直角曲杆OAB的单位长度质量为ρ,OA=AB=2l,图示瞬时以角速度ω、角加速度α绕轴O转动,该瞬时此曲杆对O轴的动量矩的大小为: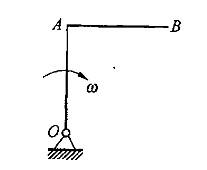
 答案:A解析:提示:根据定轴转动刚体的动量矩定义LO=JOω,JO=JOA+JAB。
答案:A解析:提示:根据定轴转动刚体的动量矩定义LO=JOω,JO=JOA+JAB。 -
第17题:
均质杆OA长L,可在铅直平面内绕水平固定轴O转动。开始杆处在如图所示的稳定平衡位置。今欲使此杆转过1/4转而转到水平位置,应给予杆的另一端A点的速度vA的大小为: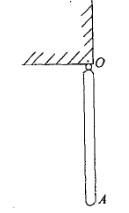
 答案:D解析:提示:应用动能定理,T2 - T1 = W12。
答案:D解析:提示:应用动能定理,T2 - T1 = W12。 -
第18题:
如图所示质量为m、长为l的均质杆OA绕O轴在铅垂平面内作定轴转动。已知某瞬时杆的角速度为ω,角加速度为α,则杆惯性力系合力的大小为( )。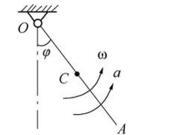
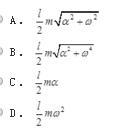 答案:B解析:
答案:B解析:
-
第19题:
当杆件AB的A端的转动刚度为3i时,杆件的B端为( )。A、自由端
B、固定端
C、铰支端
D、定向支座答案:C解析:转动刚度是指截面转动一个单位角时所需要的弯矩,不同构件的连接方式,其转动刚度是不一样的。远端铰支时,近端转动刚度为3i。 -
第20题:
均质细杆AB重力为W, A端置于光滑水平面上,B端用绳悬挂如图4-56所示。 当绳断后杆在倒地的过程中,质心C的运动轨迹为( )。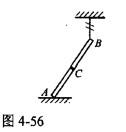
A.圆弧线 B.曲线 C.铅垂直线 D.抛物线答案:C解析:提示:水平方向质心运动守恒。 -
第21题:
均质细杆AB重力为P、长2L, A端铰支,B端用绳系住,处于水平位置,如图4-73所示。当B端绳突然剪断瞬时AB杆的角加速度大小为()。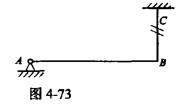
A.0 B.3g/4L C.3g/2L D.6g/L答案:B解析:提示:可用动静法,将惯性力向A点简化。 -
第22题:
单选题当杆件AB的A端的转动刚度为3i时,杆件的B端为( )。A自由端
B固定端
C铰支端
D定向支座
正确答案: C解析:
转动刚度是指截面转动一个单位角时所需要的弯矩,不同构件的连接方式,其转动刚度是不一样的。远端饺支,近端转动刚度为3i。
