设二维随机变量(X,Y)服从二维正态分布,且X～N(1,3^2),Y～N(0,4^2),且X,Y的相关系数为－,又设Z= (1)求E(Z),D(Z)；(2)求；(3)X,Z是否相互独立？为什么？

题目
设二维随机变量(X,Y)服从二维正态分布,且X～N(1,3^2),Y～N(0,4^2),且X,Y的相
　　关系数为－,又设Z=
(1)求E(Z),D(Z)；(2)求；(3)X,Z是否相互独立？为什么？

相似考题

1.两独立随机变量X和Y都服从正态分布,且X~N(3,4),Y~N(2,9)求D(X＋Y)=()。

2.设随机变量X和Y相互独立,且X~N(2,42),Y~N(3,92),则D(X＋Y)=()

3.设随机变量和是相互独立的随机变量且都服从正态分布,X~N(3,4),Y~N(2,9),求D(3X＋4Y)=()

4.设X~N(0,1),Y~N(0,1),且X与Y相互独立,则X＋Y服从的分布为()A、X+Y服从N(0，1)B、X+Y不服从正态分布C、X+Y~X2(2)D、X+Y也服从正态分布

参考答案和解析
答案：
解析：
【解】(1)

(2)
(3)因为(X，Y)服从二维正态分布，所以Z服从正态分布，同时X也服从正态分布，又X，
Z不相关，所以X，Z相互独立.
更多“设二维随机变量(X,Y)服从二维正态分布,且X～N(1,3^2),Y～N(0,4^2),且X,Y的相 ”相关问题

  • 第1题：

    设随机变量X和Y都服从正态分布,则().

    A.X+Y一定服从正态分布
    B.(X,Y)一定服从二维正态分布
    C.X与Y不相关,则X,Y相互独立
    D.若X与Y相互独立,则X-Y服从正态分布

    答案：D
    解析：
    若X,Y独立且都服从正态分布，则X,Y的任意线性组合也服从正态分布，选(D).

  • 第2题：

    设(X,Y)服从二维正态分布,其边缘分布为X～N(1,1),Y～N(2,4),X,Y的相关系数为=-0.5,且P(aX+bY≤1)=0.5,则( ).


    答案：D
    解析：
    因为(X，Y)服从二维正态分布，所以aX+bY服从正态分布，E(aX+bY)=a+2b，D(aX+bY)=a^2+4b^2+2abCov(X,Y)=a^2+4b^2-2ab,即aX+bY～N(a+2b,a^2+4b^2-2ab),由P(aX+bY≤1)=0.5得a+2b=1，所以选(D).

  • 第3题：

    设随机变量X,Y都是正态变量,且X,Y不相关,则( ).


    A.X,Y一定相互独立
    B.(X,Y)一定服从二维正态分布
    C.X,y不一定相互独立
    D.X+y服从一维正态分布


    答案：C
    解析：
    只有当(X，Y)服从二维正态分布时，X,Y独立才与X,Y不相关等价，由X,Y仅仅是正态变量且不相关不能推出X,Y相互独立，(A)不对；若X,Y都服从正态分布且相互独立，则(X，Y)服从二维正态分布，但X,Y不一定相互独立，(B)不对；当X,Y相互独立时才能推出X,Y服从一维正态分布，(D)不对，故选(C)

  • 第4题：

    设随机变量X服从正态分布N(μ，σ^2)，(σ>0)且二次方程y^2+4y+X=0无实根的概率为，则μ=________.


    答案：1、4
    解析：
    二次方程无实根，即y^2+4y+X=0的判别式16-4X<0.其概率为，即P{X>4}=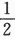，所以μ=4，答案应填4.

  • 第5题：

    设随机变量X,Y相互独立,且X～N(0,4),Y的分布律为Y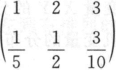～.则P(X-1-2Y≤4)=_______.


    答案：1、0.46587
    解析：
    p(X+2Y≤4)=P(Y=1)P(X≤4-2Y｜Y=1)+P(Y=2)P(X≤4-2Y｜Y=2)+P(Y=3)P(X≤4-2Y｜Y=3)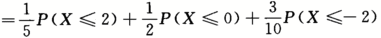

  • 第6题：

    设二维随机变量(X，Y)服从正态分布N(1，0;1，1;0)，则P{XY-Y<0}=_________.


    答案：
    解析：
    (X，Y)～N(1，0;1，1;0)，所以X与Y相互独立，且X～N(1，1)，Y～N(0，1)也就有(X-1)～N(0，1)与Y相互独立，再根据对称性：P{X-1<0}=P{X-1>0}=P(Y<0)=P{Y>0}=.不难求出P{XY-Y<0}的值.

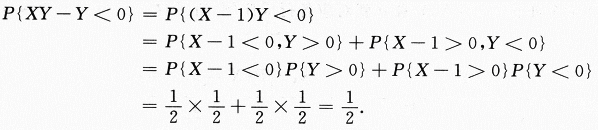
  • 第7题：

    已知随机变量X服从正态分布N(μ，σ2)，设随机变量Y=2X，那么Y服从的分布是()。


    A.N(2μ，2σ2)

    B.N(4μ，4σ2)

    C.N(2μ，4σ2)

    D.N(μ，σ2)

    答案：C
    解析：
    由于随机变量X服从正态分布N(μ，σ2)，则随机变量Y=2X的均值为2μ，方差为4σ2，即Y服从的分布是N(2μ，4σ2)。

  • 第8题：

    设随机变量X服从正态分布N（1，2），Y服从泊松分布P（2）。求期望E=（2X—y+3）。


    答案：
    解析：
    解：本题考查一些重要分布的数字特征与参数之间的关系。E（X）=1，E（y）=2 E（2X-y+3）=2E（X）-E（y）+3=3。

  • 第9题：

    设X，Y是相互独立的随机变量，X~N（2，σ2），Y~N（-3，σ2），且P{|2X+Y-1|≤8.7654}=0.95，则σ=（）。


    正确答案:2

  • 第10题：

    若随机变量X～N（0，4），Y～N（－1，5），且X与Y相互独立。设Z＝X＋Y－3，则Z～（）。


    正确答案:N（－4，9）

  • 第11题：

    单选题
    设随机变量X～N（0，1），Y～N（0，4），且相关系数ρXY=1，则（　　）.
    A

    P{Y=-2X-1}=1

    B

    P{Y=2X-1}=1

    C

    P{Y=-2X+1}=1

    D

    P{Y=2X+1}=1


    正确答案： B
    解析：
    令Y=aX+b，因为X～N（0，1），Y～N（1，4），则EY=aEX+b=1，得b=1，
    D（Y）=a2D2（X）=4，则a=±2.
    又ρXY=1，则a＞0，故a=2.
    故应选D.

  • 第12题：

    单选题
    设随机变量（X，Y）服从二维正态分布，且X与Y不相关，fX（x），fY（y）分别表示X，Y的概率密度，则在Y＝y的条件下，X的条件概率密度fX|Y（x|y）为（　　）。
    A

    fX（x）

    B

    fY（y）

    C

    fX（x）fY（y）

    D

    fX（x）/fY（y）


    正确答案： D
    解析：
    因为（X，Y）服从二维正态分布，且相关系数ρ＝0，故X，Y相互独立，故fX|Y（x|y）＝f（x，y）/fY（y）＝fX（x）fY（y）/fY（y）＝fX（x）。

  • 第13题：

    设二维随机变量(X，Y)服从二维正态分布，则随机变量ζ=X+Y与η=X-Y不相关的充分必要条件为


    答案：B
    解析：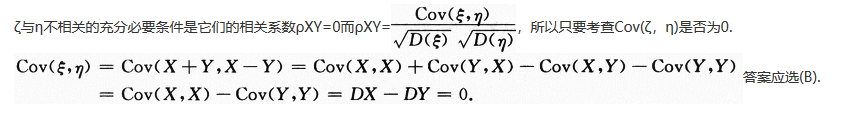

  • 第14题：

    设随机变量X,Y相互独立,且X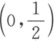～N,Y～N,则与Z=Y-X同分布的随机变量是().

    A.X-Y
    B.X+Y
    C.X-2Y
    D.Y-2X

    答案：B
    解析：
    Z=Y-X～N(1,1)，因为X-Y～N(-1,1),X+Y～N(1,1).X-2Y～N，Y-2X～N，所以选(B).

  • 第15题：

    设随机变量X,Y,Z相互独立,且X～U［-1,3］,Y～B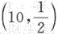,Z～N(1,3……2),且随机变量U=X+2Y-32+2,则D(U)=_______.


    答案：
    解析：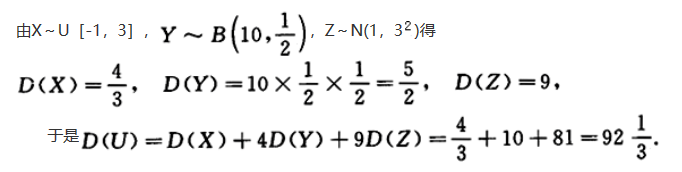

  • 第16题：

    设随机变量X～N(0,σ^2),Y～N(0,4σ^2),且P(X≤1,y≤-2)=,则P（X>1,Y>-2）=_______.


    答案：
    解析：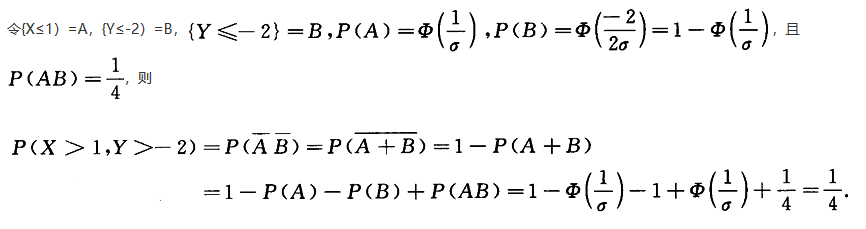

  • 第17题：

    设二维随机变量(X，Y)服从正态分布N(μ，μ；σ^2，σ^2；0)，则E(XY^2)=________.


    答案：
    解析：

  • 第18题：

    设随机变量(X，Y)服从二维正态分布，其概率密度为f(x,y)=1/2π


    答案：A
    解析：
    提示 (X，Y)~N(0，0，1，1，0)，X~N(0，1)，Y~N(0，1)，E(X2+Y2) =E(X2)+E(Y2)，E(X2)=D(X) + (E(X) )2

  • 第19题：

    设随机变量X，Y相互独立，且X～N(μ，σ2)，Y在[a，b]区间上服从均匀分布，则D(X-2Y)=()。



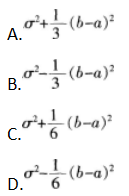    答案：A
    解析：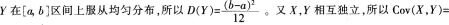

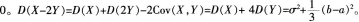
  • 第20题：

    设随机变量X服从正态分布N（μ1，σ21），随机变量Y服从正态分布N（μ2，σ22），且P{|X-μ1|<1}>P{|Y-μ2|<1}，则必有（）

    • A、σ1<σ2
    • B、σ1>σ2
    • C、μ1<μ2
    • D、μ1>μ2

    正确答案:A

  • 第21题：

    若随机变量X与Y相互独立，且X服从N（1，9），Y服从N（2，6），则X+Y服从（）分布。


    正确答案:N（3，25）

  • 第22题：

    填空题
    设随机变量X服从正态分布N（μ，σ2）（σ＞0），且二次方程y2＋4y＋X＝0无实根的概率为0.5，则μ＝____。

    正确答案： 4
    解析：
    令Y＝（X－μ）/σ，则Y服从标准正态分布N（0，1）。
    该二次方程无实根的充要条件为4－X＜0，根据题意，有：
    0.5＝P{X＞4}＝1－P{X≤4}＝1－P{（X－μ）/σ≤（4－μ）/σ}＝1－P{Y≤（4－μ）/σ}＝1－Φ[（4－μ）/σ]，即Φ[（4－μ）/σ]＝0.5，故（4－μ）/σ＝0，μ＝4。

  • 第23题：

    单选题
    设随机变量X服从正态分布N（μ1，σ12），Y服从正态分布N（μ2，σ22），且P{|X－μ1|＜1}＞P{|Y－μ2|＜1}，则必有（　　）。
    A

    σ1＜σ2

    B

    σ1＞σ2

    C

    μ1＜μ2

    D

    μ1＞μ2


    正确答案： A
    解析：
    根据题意，有：P{|（X－μ1）/σ1|＜1/σ1}＞P{|（Y－μ2）/σ2|＜1/σ2}，故1/σ1＞1/σ2⇒σ1＜σ2。

相关内容