老王围着边长为50米的正六边形的草地跑步，他从某个角点出发，按顺时钟方向跑了500米，距出发点直线距离多少米？（ ）

题目
老王围着边长为50米的正六边形的草地跑步，他从某个角点出发，按顺时钟方向跑了500米，距出发点直线距离多少米？（ ）

相似考题

1.某日小明在一条南北方向的公路上跑步，他从A地出发，每隔10min记录下自己的跑步情况（向南为正方向，单位：m）：-1008, 1100，-976, 1010，-827, 946 1h后他停下来休息，此时他在A地的什么方向？距A地多远？小明共跑了多少米？

2.老王围着边长为50米的正六边形的草地跑步，他从某个角点出发，按顺时钟方向跑了500米，距出发点直线距离多少米？（ ）

3.甲和乙在长400米的环形跑道上匀速跑步，如两人同时从同一点出发相向而行．则第一次相遇的位置距离出发点有l50米的路程；如两人同时从同一点出发同向而行，跑得快的人第一次追上另一人时跑了（　　）米。A.600 B.800 C.1000 D.1200

4.一个正六边形跑道，每边长为100米，甲乙两人分别从两个相对的顶点同时出发，沿跑道相向匀速前进。第一次相遇时甲比乙多跑了60米，问甲跑完三圈时，两人之间的直线距离是多少？（ ）A．100米 B．150米 C．200米 D．300米

参考答案和解析
答案：B
解析：
每边长度为50米，共计跑了10段线路，因此将跑到与出发点相间的位置，两点之间的直线距离为
。
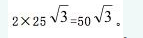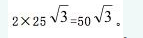正确答案为B。
更多“老王围着边长为50米的正六边形的草地跑步，他从某个角点出发，按顺时钟方向跑了500米，距出发点直线距离多少米？（ ）”相关问题

  • 第1题：

    甲和乙在长400米的环形跑道上匀速跑步，如两人同时从同一点出发相向而行，则第一次相遇的位置距离出发点有150米的路程；如两人同时从同一点出发同向而行，问跑得快的人第一次追上另一人时跑了多少米？( )

    A. 600
    B. 800
    C. 1000
    D. 1200

    答案：C
    解析：
    行程问题。相遇地点距离出发点150米的距离，则另外一个人走了250米，所走的快的人每走250米就会比慢的人多走100米，如果同向运动，则想要快的追上慢的就要正好扣圈多走400米，则走的快的要步行1000米的距离才能追上。

  • 第2题：

    已知正六边形ABCDEF的边长为a，PA为过点A而垂直于正六边形所在平面M的垂线，且PA=a，求：
    (I)点P到AB、BC、CD各边的距离；
    (II)PD与平面M所成的角．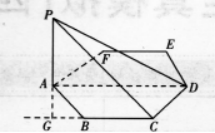


    答案：
    解析：
    (I)如图所示，
    24题答案图
    ∵PA上平面M，∴PA上BC，
    ∴点P到AB的距离为a．过A作BC的垂线交CB的延长线于G，连结PG，
    ∴BC上平面APG，即PG⊥AB，


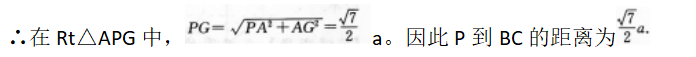
    ∵PA上平面M，
    ∴AC是PC在平面M上的射影，
    又∵AD是正六边形ABCDEF外接圆的直径，
    ∴∠ACD=90o．
    因此AC⊥CD，所以CD⊥平面ACP，即PC是P到CD的距离，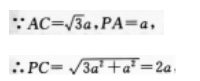

    因此P到CD的距离为2a．
    (Ⅱ)设PD与DA所夹的角为口，在Rt△PAD中，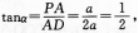

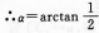    (VI)为PD与平面M所夹的角．

  • 第3题：

    单选题
    一个正六边形跑道，每边长为100米，甲乙两人分别从两个相对的顶点同时出发，沿跑道相向匀速前进，第一次相遇时甲比乙多跑了60米，则甲跑三圈时，两人之间的直线距离是多少？（　　）
    A

    100米

    B

    150米

    C

    200米

    D

    300米


    正确答案： B
    解析：
    第一次相遇时甲比乙多跑60米，则相遇时乙跑了（300－60）÷2＝120米，甲跑了180米，两者的速度比为180:120。设甲跑了三圈时，乙跑过的距离为x，180:120＝（60×3）:x，得x＝1200，刚好为两圈。因此甲跑三圈时，两人都回到自己的出发点，即为相对的顶点，其直线距离为200米。

  • 第4题：

    A、B两地相距400米，早上8点小周和老王同时从A地出发在A、B两地间往返锻炼。小周每分钟跑200米，老王每分钟走80米，问8点11分，小周和老王之间的距离是多少米？

    A. 0
    B. 80
    C. 120
    D. 200

    答案：C
    解析：
    小周每分钟走200米，全程是400米，11分钟小周正好在AB中点处，距A点200米，老王每分钟走80米，11分钟走了880米，即一个往返又走了80米，距A点80米，因此两人相距120米。

  • 第5题：

    单选题
    一条圆形跑道长500米，甲、乙两人从不同起点同时出发，均沿顺时针方向匀速跑步。已知甲跑了600米后第一次追上乙，此后甲加速20%继续前进，又跑了1200米后第二次追上乙。问甲出发后多少米第一次到达乙的出发点？（　　）
    A

    180

    B

    150

    C

    120

    D

    100


    正确答案： A
    解析：
    赋值甲的速度为100米/分，第一次追及，甲跑了600米，用时为6分；第二次追及，甲加速20%，即速度为120米/分，又跑了1200米，用时为10分。行程问题追及公式为：S差＝v差t，从第一次追及开始，到第二次追及时，两人的路程差为1圈，即500＝（120－v乙）×10，解得v乙＝70米/分。分析第一次追及过程可知，甲比乙多走的距离即为甲出发点到乙出发点距离，S差＝v差t＝（100－70）×6＝180米。故正确答案为A。

相关内容