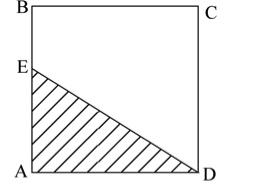
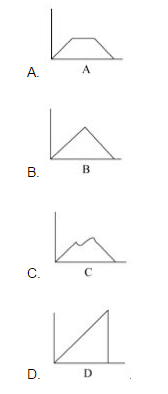
如下图,正方形ABCD边长为10厘米,一只小蚂蚁E从A点出发均速移动,沿边AB、BC、CD前往D点。问哪个图形反映了三角形AED的面积与小蚂蚁行走时间的关系?
题目
如下图,正方形ABCD边长为10厘米,一只小蚂蚁E从A点出发均速移动,沿边AB、BC、CD前往D点。问哪个图形反映了三角形AED的面积与小蚂蚁行走时间的关系?


相似考题
更多“如下图,正方形ABCD边长为10厘米,一只小蚂蚁E从A点出发均速移动,沿边AB、BC、CD前往D点。问哪个图形反映了三角形AED的面积与小蚂蚁行走时间的关系? ”相关问题
-
第1题:
如图,边长为a的正方形ABCD中,点E是对角线BD上的一点,且BE=BC,点P在EC上,PM⊥BD于M,PN⊥BC于N,则PM+PN=________。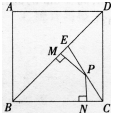 答案:解析:
答案:解析: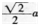
解析:作EK⊥BC于K,连接BP,由△EBC的面积等于△PBE和△PBC的面积之和且BE=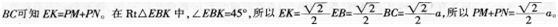
-
第2题:
下图中正方形的边长为6em,已知正三角形覆盖了正方形1/2的面积,正方形覆盖了正三角形3/4的面积。三角形的面积为( ) cm2。 A.18
A.18
B.20
C.24
D.36答案:C解析:正方形面积为6x6=36,则覆盖面积为36÷2=18,所以三角形面积为18÷3/4-=24. -
第3题:
下图给定的平面图折叠后的立体图形是______。
 A.A
A.A
B.B
C.C
D.D答案:A解析:将原展开图标上序号如下图, 逐一进行分析。

A 项: 选项与题干一致, 当选;
B 项: 选项中的面 k 在展开图中没有出现, 选项与题干不一致, 排除;

C 项: 选项中包括面 e 和面 i, 而面 e 和面 i 为相对面, 不能同时出现, 选项与题干不一致, 排除;
D 项: 选项中包括面 f 和面 h, 而面 f 和面 h 为相对面, 不能同时出现, 选项与题干不一致, 排除。 -
第4题:
如下图所示,正方形ABCD的边长为5cm,AC、BD分别是以点D和点C为圆心、 5cm为半径作的圆弧。问阴影部分a的面积比阴影部分b小多少?(π取3. 14)( )
A. 13.75cm2 B. 14. 25cm2
C. 14. 75cm2 D. 15. 25cm2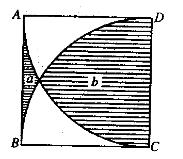 答案:B解析:几何问题,利用容斥原理进行求解。分析题干可知,两个1/4圆覆盖的区城面积减去阴影部分b的面积再加上阴影部分a的面积等于正方形的面积,所以得到1/4X3.14X52X2-b+a=52,b-a = 14.25(cm2)。
答案:B解析:几何问题,利用容斥原理进行求解。分析题干可知,两个1/4圆覆盖的区城面积减去阴影部分b的面积再加上阴影部分a的面积等于正方形的面积,所以得到1/4X3.14X52X2-b+a=52,b-a = 14.25(cm2)。 -
第5题:
下列图形中箭头所指的"点"违背了westgard基本质控规则中的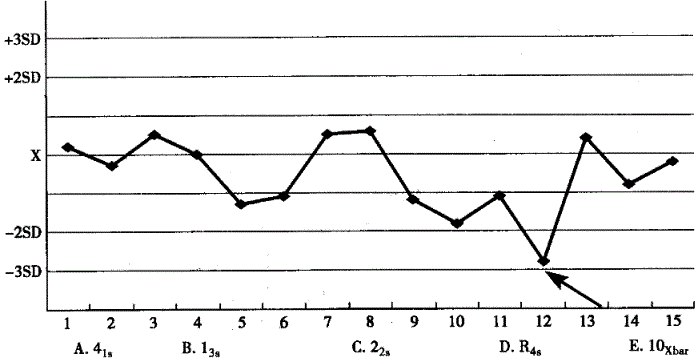 A.A
A.A
B.B
C.C
D.D
E.E答案:A解析:westgard推荐下列6个基本质控规则,其定义如下:①1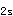 :一个质控测定值超过
:一个质控测定值超过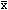 ±2s质控限,作为警告;②1
±2s质控限,作为警告;②1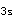 :一个质控测定值超过
:一个质控测定值超过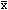 ±3s质控限,则判断为该分析批失控;③2
±3s质控限,则判断为该分析批失控;③2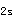 :当两个连续的质控测定值同时超过
:当两个连续的质控测定值同时超过 +2s或
+2s或 -2s,则判断为失控,这两个测定值可以来自同一个质控物,也可以是两个不同的质控物;④R
-2s,则判断为失控,这两个测定值可以来自同一个质控物,也可以是两个不同的质控物;④R :当同一批内高和低的质控测定值之间的差或极差超过4s时,则判断为失控;⑤4当4个连续的质控测定值同时超过
:当同一批内高和低的质控测定值之间的差或极差超过4s时,则判断为失控;⑤4当4个连续的质控测定值同时超过 +1s或
+1s或 -h,则判断为失控;⑥10
-h,则判断为失控;⑥10 :当10个连续的质控测定值落在平均值的同一侧,则判断为失控。
:当10个连续的质控测定值落在平均值的同一侧,则判断为失控。 -
第6题:
若正方形ABCD的边长为4,E为BC边上一点,BE=3,M为线段AE上的一点,射线BM交正方形的一边于点F,且BF=AE,则BM的长为5/2或12/5。
正确答案:错误 -
第7题:
单选题一正三角形小路如下图所示,甲、乙两人同时从A点出发,朝不同方向沿小路散步,已知甲的速度是乙的2倍。问以下哪个坐标图能准确描述两人之间的直线距离与时间的关系(横轴为时间,纵轴为直线距离):AB.
BD.
正确答案: A解析: -
第8题:
如右图,正方形的迷你轨道边长为1米,1号电子机器人从点A以1米/秒的速度顺时针绕轨道移动,2号电子机器人从点A以3米/秒的速度逆时针绕轨道移动,则它们的第2017次相遇在: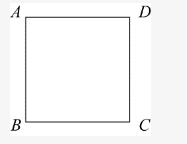 A.点A
A.点A
B.点C
C.点B
D.点D答案:D解析:第一步,本题考查行程问题,属于相遇追及类。
第二步,第1秒1号机器人顺时针走到点D,2号逆时针走到点D,故两个机器人每过1秒相遇一次,相遇点依次为D—C—B—A—D—C—B—A……每4次相遇为一个周期。
第三步,2017÷4=504…1,则第2017次相遇与第1次相遇地点是同一地点,即D点。 -
第9题:
如下图所示,正方形A B C D 的边长是14厘米,其中,B E=C E=7厘米。如果点P以每秒2厘米的速度沿着边线C D 从点C 出发到点D ,那么三角形A EP的面积将以每秒多少平方厘米的速度增加: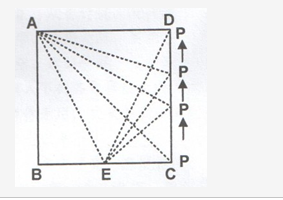
A 7
B 8
C 9
D 10答案:A解析:
-
第10题:
下图中ABCD为边长10米的正方形路线,E为AD中点,F为与B相距3米的BC上一点,从E点到F点有小路EGHF,小路的每一段都与AB垂直或平行,且GH相距2米。甲经EABF从E点匀速运动到F点用时9秒,则其以相同速度经EGHF从E点匀速运动到F点用时多少秒? A.12
A.12
B.10
C.9
D.8答案:D解析:第一步,本题考查行程问题,属于基本行程类。
第二步,E为AD中点,则EA=10÷2=5(米),甲经过EABF从E点到F点所走路程为AE+AB+BF=5+10+3=18(米);标记HF的转弯点为M、N,那么甲经EGHF从E点到F点所走路程为EG+GH+HM+MN+NF=(EG+HM+NF)+GH+MN=10+2+(5+2-3)=16(米)。
第三步,两种路线速度相同,路程比为18∶16=9∶8,那么所用时间之比为9∶8,第一种路线用时9秒,那么第二种路线用时8秒。
因此,选择D选项。 -
第11题:
如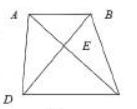 ,在四边形ABCD中,AB//CD,AB与CD的边长分别为4和8,若ABE的面积为4,则四边形ABCD的面积为( )A.24
,在四边形ABCD中,AB//CD,AB与CD的边长分别为4和8,若ABE的面积为4,则四边形ABCD的面积为( )A.24
B.30
C.32
D.36
E.40答案:D解析: -
第12题:
在矩形ABCD中,AB=16cm,AD=6cm,动点P、Q分别从A、C两处出发,点P以3cm/s的速度向点B移动,一直到点曰,点Q以2cm/s向D移动,当P,Q距离为10cm时,P、Q两点从出发开始经过时间为( )s。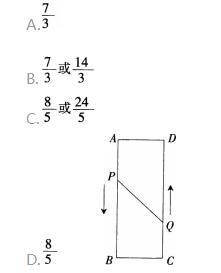 答案:C解析:
答案:C解析:
-
第13题:
判断题若正方形ABCD的边长为4,E为BC边上一点,BE=3,M为线段AE上的一点,射线BM交正方形的一边于点F,且BF=AE,则BM的长为5/2或12/5。A对
B错
正确答案: 错解析: 暂无解析
