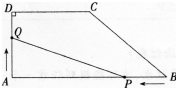
如图。在直角梯形ABCD中，AB∥CD，∠BAD=90o，且AB=8，AD=3，CD=4，动点P，Q分别以点B和点A为起点同时出发，点P沿B→A，以每秒1个单位速度运动，终点为点A；点Q沿A→D→C→B，以每秒1.5个单位速度运动，终点为点B。设△APQ的面积为y，运动时间为x。 (1)求y关于x的函数解析式y=f(x)； (2)画出函数y=f(x)的图象。

第1题：

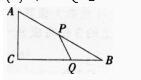
如图，在Rt△ABC中，∠C=90o,AC=6，BC=8，动点P由起点A沿边AB向终点B运动，每秒2个单位，动点Q由起点B沿边BC向终点C运动，每秒1个单位，P、Q两点同时由起点开始运动，记运动时间为t秒。
(1)设△BPQ的面积为S，求S的最大值：
(2)当△BPQ与△ABC相似时，求t的值。

答案：

解析：

第2题：

下图中ABCD为边长10米的正方形路线，E为AD中点，F为与B相距3米的BC上一点，从E点到F点有小路EGHF，小路的每一段都与AB垂直或平行，且GH相距2米。甲经EABF从E点匀速运动到F点用时9秒，则其以相同速度经EGHF从E点匀速运动到F点用时多少秒？

A.12
B.10
C.9
D.8

第3题：

以固定点电荷P为圆心作两个同心圆，如图4虚线所示。带电粒子Q在P的电场中运动轨迹与两圆在同一平面内，a．b、c为轨迹上的三个点，其在a．b、c三点的加速度大小分别为Aa、Ab、Ac，速度大小分别为Va、Vb、Vc、则( )。

答案：D

解析：

第4题：

在直角三角形ABC中，点D是斜边AB的中点，点P为线段CD的中点，则( )。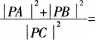

A、2
B、4
C、5
D、10

答案：D

解析：

本题主要考查两点问的距离公式，以及坐标法这一重要的解题方法和数形结合的数学思

第5题：

如图4-48所示直角弯杆OAB以匀角速度ω绕O轴转动，并带动小环M沿OD杆运动。已知OA=l,取小环M为动点，OAB杆为动系，当 φ =60°时，M点牵连加速度ae的大小为（ ）。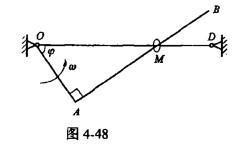

答案：D

解析：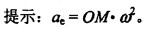

第6题：

某构件受力简图如图，则点O的力矩Mo为()。

A、P.a
B、P.b
C、P.c
D、P.d

第7题：

如图，在一张矩形纸片ABCD中，AB=4，BC=8。点E，F分别在AD，BC上，将纸片ABCD沿直线EF折叠，点C落在AD上的一点日处，点D落在G处，有以下四个结论：①四边形CFHE是菱形；②EC平分∠DCH；③线段BF的取值范围为3≤BF≤4；④当点H与点A重合时, 。以上结论中，你认为正确的有( )个。

A.1
B.2
C.3
D.4

答案：C

解析：

第8题：

汽车由静止开始从A点沿直线ABC作匀变速直线运动，第4s末通过B点时关闭发动机，再经6s到达C点时停止。已知AC的长度为30m，则下列说法正确的是（）

• A、通过B点时速度的3m/s
• B、通过B点时速度是6m/s
• C、AB的长度为12m
• D、汽车在AB段和BC段的平均速度相同

第9题：

设秆AB无限长，它与CD的延长线交于点P，则下列说法不正确的是（）

• A、点P的瞬时速度为零
• B、点P的瞬时速度必不为零，其速度矢端在直线AB上
• C、点P的瞬时速度瞬时必不为零，其速度矢端必在CD的延长线上
• D、点P的瞬时速度瞬时必不为零，其速度矢端既不在直线AB上也不在CD的延长线上

第10题：

一质点沿半径为R的圆周运动，在t=0时经过P点，此后它的速率v按v=A+Bt（A，B为正的已知常量）变化，则质点沿圆周运动一周再经过P点时的切向加速度a_t=（），法向加速度（）。

第11题：

下述各种情况下，动点的全加速度a、切向加速度a_t和法向加速度a_n三个矢量之间正确的是（）。 （1）点沿曲线作匀速运动。 （2）点沿曲线运动，在该瞬时其速度为零。 （3）点沿直线作变速运动。 （4）点沿曲线作变速运动。

• A、（1）中必恒有a_n=0，a=a_t
• B、（2）中该瞬时必有a_n=0，a=a_t
• C、（3）中必恒有a≡0
• D、（4）中必恒有a_t=0，a=a_n

第12题：

第13题：

如图，在△ABC中，AC=8，BC=6，∠ACB=90°，动点P以每秒一个单位的速度从点A出发，沿着边AC向点C移动，同时，动点Q以相同的速度从点B出发，沿着边BA向点A移动，设P，Q两点移动时间为t秒(0≤t≤8)。



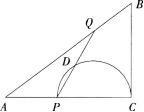
(1)当t为何值时，△APQ的面积最大 最大值是多少
(2)以PC为直径的半圆交PQ于点D，是否存在t，使得PD=DQ 若存在，求出t的值，若不存在说明理由。

答案：

解析：

(1)如图，作QH⊥AC，则QH∥BC，

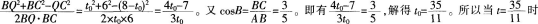
第14题：

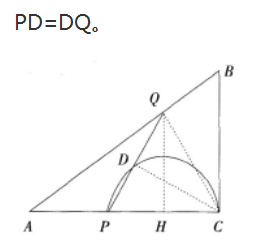
如图，ABCD为矩形，AB=4，BC=3，边CD在直线L上，将矩形ABCD沿直线L作无滑动翻转，当点A第一次翻转到点A1位置时，点A经过的路线长为：



A7π
B6π
C3π
D3π/2

答案：B

解析：

第15题：

如图，将带正电的小球A固定，另一带电小球B从A附近的P点处由静止释放，其下落到Q点的运动轨迹如虚线所示，不计空气阻力，则小球B（　　）。

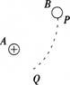A．可能带正电
B．在Q点的速度大于在P点的速度
C．在Q点的电势能大于在P点的电势能
D．从P到Q，重力势能的减少量大于动能的增加量

第16题：

已知点沿半径为40cm的圆周运动，其运动规律为s=20t（s以厘米计，t以秒计）。 若t=ls，则点的速度与加速度的大小为（ ）。

答案：B

解析：

提示：点的速度、切向加速度和法向加速度分别为：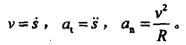

第17题：

横波以波速u沿x轴正向传播，t时刻波形曲线如图2-9所示，则该时刻（ ）。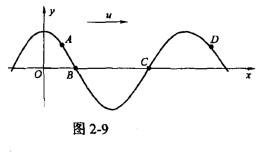

A. A点速度小于零 B. B点静止不动 C. C点向上运动 D. D点速度大于零

第18题：

如图是半径为2，圆心角为90°的直角扇形OAB，Q为弧AB上任意一点，点P在扇形内(含边界)，

答案：

解析：

第19题：

在矩形ABCD中，AB=16cm，AD=6cm，动点P、Q分别从A、C两处出发，点P以3cm/s的速度向点B移动，一直到点曰，点Q以2cm／s向D移动，当P,Q距离为10cm时，P、Q两点从出发开始经过时间为( )s。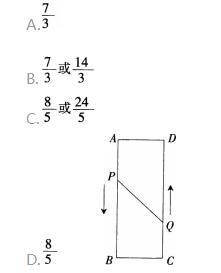

答案：C

解析：

第20题：

P、Q、R三点在同一条直线上，一物体从P点静止开始做匀加速直线运动，经过Q点的速度为v，到达R点的速度为3v，则PQ∶QR等于（）

• A、1∶3
• B、1∶6
• C、1∶5
• D、1∶8

第21题：

已知点沿其轨迹的运动方程为s=b+ct，式中b、c均为常量，则（）

• A、点的轨迹必为直线；
• B、点的轨迹必为曲线；
• C、点必作匀速运动；
• D、点的加速度必为零。

第22题：

建立刚体平面运动的运动方程时，下述说法正确的是（）

• A、必须以速度为零的点为基点
• B、必须以加速度为零的点为基点
• C、必须以加速度和速度都为零的点为基点
• D、基点可以任意选取

第23题：