若正方形ABCD的边长为4，E为BC边上一点，BE＝3，M为线段AE上一点，射线BM交正方形的一边于点F，且BF＝AE，则BM的长为______________ ．

题目

若正方形ABCD的边长为4，E为BC边上一点，BE＝3，M为线段AE上一点，射线BM交正方形的一边于点F，且BF＝AE，则BM的长为______________ ．

相似考题

1.请教:2009年黑龙江省哈尔滨市中考《数学》试卷第2大题第9小题如何解答?【题目描述】18．若正方形ABCD的边长为4，E为BC边上一点，BE＝3，M为线段AE上一点，射线BM交正方形的一边于点F，且BF＝AE，则BM的长为______________ ．

2.如图，面积为20的正方形ABCD中，有一个小正方形EFGH，其中E，F，G分别在AB，BC，FD上，若BF=√5/2，则小正方形的周长是()。 A.5√5/8 B.5√5/6 C.5√5/2 D.10√5/3

3.如图，边长为a的正方形ABCD中，点E是对角线BD上的一点，且BE=BC，点P在EC上，PM⊥BD于M，PN⊥BC于N，则PM+PN=________。

4.如图所示，点P为正方形ABCD内一点，且PA=1，PB=2,PC=3试求∠ABP的度数？

更多“若正方形ABCD的边长为4,E为BC边上一点,BE=3,M为线段AE上一点,射线BM交正方形的一边于点F,且BF ”相关问题

  • 第1题：

    平行四边形ABCD如右图所示，E为AB上的一点，F、G分别是AC和DE、DB的交点。若AB=3AE，则四边形BEFG与ABCD的面积之比是：

    A.2︰7
    B.3︰13
    C.4︰19
    D.5︰24

    答案：D
    解析：
    第一步，本题考查几何问题，属于平面几何类，用赋值法解题。
    第二步，题干没给出具体数值，可以采用赋值法解题。赋值AB=3，平行四边形ABCD的高为4，则AE=1；由于△AEF相似于△CDF，则两个三角形的高之比为AE：DC=1︰3，可知△AEF的高为
    4*1/4=1。△ABG与△CDG全等，则△ABG的高为4÷2=2。
    第三步，四边形BEFG面积=△ABG面积-△AEF面积=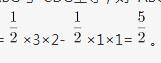

    四边形ABCD面积=3×4=12，两者之比为 ︰12=5︰24。
    因此，选择D选项。

  • 第2题：

    图6-18是一个边长为10的正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,则阴影部分的面积为（ ）




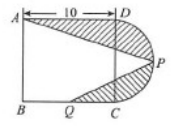
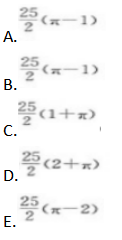    答案：C
    解析：

  • 第3题：

    如图，在一张矩形纸片ABCD中，AB=4，BC=8。点E，F分别在AD，BC上，将纸片ABCD沿直线EF折叠，点C落在AD上的一点日处，点D落在G处，有以下四个结论：①四边形CFHE是菱形；②EC平分∠DCH；③线段BF的取值范围为3≤BF≤4；④当点H与点A重合时, 。以上结论中，你认为正确的有( )个。

    A.1
    B.2
    C.3
    D.4

    答案：C
    解析：

  • 第4题：

    下图中ABCD为边长10米的正方形路线，E为AD中点，F为与B相距3米的BC上一点，从E点到F点有小路EGHF，小路的每一段都与AB垂直或平行，且GH相距2米。甲经EABF从E点匀速运动到F点用时9秒，则其以相同速度经EGHF从E点匀速运动到F点用时多少秒？

    A.12
    B.10
    C.9
    D.8

    答案：D
    解析：
    第一步，本题考查行程问题，属于基本行程类。
    第二步，E为AD中点，则EA＝10÷2＝5（米），甲经过EABF从E点到F点所走路程为AE＋AB＋BF＝5＋10＋3＝18（米）；标记HF的转弯点为M、N，那么甲经EGHF从E点到F点所走路程为EG＋GH＋HM＋MN＋NF＝（EG＋HM＋NF）＋GH＋MN＝10＋2＋（5＋2－3）＝16（米）。
    第三步，两种路线速度相同，路程比为18∶16＝9∶8，那么所用时间之比为9∶8，第一种路线用时9秒，那么第二种路线用时8秒。
    因此，选择D选项。

  • 第5题：

    已知△ABC的三边长AC＝3，BC＝4，AB＝5，P为AB边上任意一点，则CP→ (BA→－BC→)的最大值为(　　)

    A、8
    B、9
    C、12
    D、15

    答案：B
    解析：

相关内容