如图，边长为a的正方形ABCD中，点E是对角线BD上的一点，且BE=BC，点P在EC上，PM⊥BD于M，PN⊥BC于N，则PM+PN=________。

题目
如图，边长为a的正方形ABCD中，点E是对角线BD上的一点，且BE=BC，点P在EC上，PM⊥BD于M，PN⊥BC于N，则PM+PN=________。

相似考题

1.请教:2009年黑龙江省哈尔滨市中考《数学》试卷第2大题第9小题如何解答?【题目描述】18．若正方形ABCD的边长为4，E为BC边上一点，BE＝3，M为线段AE上一点，射线BM交正方形的一边于点F，且BF＝AE，则BM的长为______________ ．

2.设M、N都是自然数，记PM是自然数M的各位数字之和，PN是自然数N的各位数字之和。又记M*N是M除以N的余数。已知M+N=4084，那么(PM+PN)*9的值是( )。A．7B．9C．0D．5

3.如图所示，点P为正方形ABCD内一点，且PA=1，PB=2,PC=3试求∠ABP的度数？

4.若正方形ABCD的边长为4，E为BC边上一点，BE＝3，M为线段AE上一点，射线BM交正方形的一边于点F，且BF＝AE，则BM的长为______________ ．

更多“如图，边长为a的正方形ABCD中，点E是对角线BD上的一点，且BE=BC，点P在EC上，PM⊥BD于M，PN⊥BC于N，则PM+PN=________。 ”相关问题

  • 第1题：

    (6分)如图，点P为矩形ABCD边BC上一点(不包括端点)，E为BC延长线上一点，CQ为∠DCE的角平分线，连接AP，PQ，使AP⊥PQ。求证：当AB=BC时，存在AP=PQ。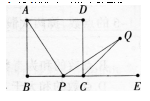


    答案：
    解析：

    ∴AP=PQ。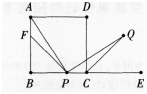

  • 第2题：

    如图，平行四边形ABCD，∠ADC的角平分线DE交BC于E,且AD=14，DC=9，则BE/EC的值为()。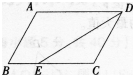

    A.1/3
    B.4/9
    C.5/9
    D.2/3

    答案：C
    解析：
    AD∥BC，则∠ADE=∠DEC，又∠ADE=∠CDE，所以△CDE为等腰三角形，EC=CD=9，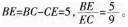

  • 第3题：

    如图所示，梯形ABCD的两条对角线AD、BC相交于O，EF平行于两条边且过O点。现已知AB=6，CD=18。问EF的长度为多少？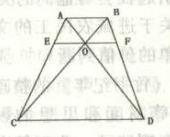


    A. 8.5
    B. 9
    C. 9.5
    D. 10

    答案：B
    解析：
    解题指导： 18*BF/BD=6*DF/BD， BF/DF＝1：3， OF/CD=1:4， OE/CD=1:4， EF=CD/2＝9，故答案为B。

  • 第4题：

    下图中ABCD为边长10米的正方形路线，E为AD中点，F为与B相距3米的BC上一点，从E点到F点有小路EGHF，小路的每一段都与AB垂直或平行，且GH相距2米。甲经EABF从E点匀速运动到F点用时9秒，则其以相同速度经EGHF从E点匀速运动到F点用时多少秒？

    A.12
    B.10
    C.9
    D.8

    答案：D
    解析：
    第一步，本题考查行程问题，属于基本行程类。
    第二步，E为AD中点，则EA＝10÷2＝5（米），甲经过EABF从E点到F点所走路程为AE＋AB＋BF＝5＋10＋3＝18（米）；标记HF的转弯点为M、N，那么甲经EGHF从E点到F点所走路程为EG＋GH＋HM＋MN＋NF＝（EG＋HM＋NF）＋GH＋MN＝10＋2＋（5＋2－3）＝16（米）。
    第三步，两种路线速度相同，路程比为18∶16＝9∶8，那么所用时间之比为9∶8，第一种路线用时9秒，那么第二种路线用时8秒。
    因此，选择D选项。

  • 第5题：

    设P是圆x2+y2=2上的一点，该圆在点P的切线平行于直线x+y+2=0，则点P的坐标为



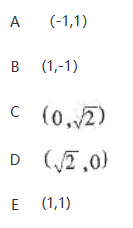    答案：E
    解析：

  • 第6题：

    如图6-9所示,在△ABC中,AD⊥BC于D点,BD=CD,若BC=6,AD=5,则图中阴影部分的面积为（ ）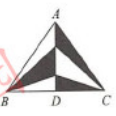

    A.3
    B.7.5
    C.15
    D.30
    E.5.5

    答案：B
    解析：

  • 第7题：

    如右图所示，梯形ABCD的对角线AC丄BD，其中AD=1/2，BC=3，AC=2，BD=2.1，则梯形ABCD的髙AE的值是()。



    答案：C
    解析：
    由ACXBD=(AD+BC)XAE=>AE=42/45。

  • 第8题：

    如图6，AB是⊙E的直径，C是直线AB上一点，CD切⊙E于点D，且∠A=25o，则∠C= ______度。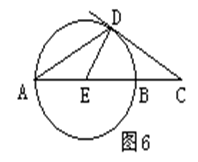


    答案：
    解析：
    40

  • 第9题：

    分别用分析法，综合法证明如下命题。
    命题：如图：三角形ABC的角B和角C的角平分线相交于点0，过点O作平行于底边BC的直线，交AB边于点D，交AC边于点E，则DE=BD+EC。



    答案：
    解析：
    证明：(1)分析法证明：要证DE=BD+EC．
    需证OD=BD，OE=CE，
    需证∠DBO=∠DOB,∠ECO=∠EOC，
    显然由已知OB为∠DBC的平分线，OC为∠ECB的平分线，且DE∥BC，所以∠DBO=∠DOB,∠ECO=∠EOC,所以命题成立。
    (2)综合法证明：
    ∵OB为∠DBC的平分线，OC为1ECB的平分线，且DE∥BC，
    ∴∠DBO=∠OBC=∠DOB,∠EC0=∠BC0=∠EOC,
    ∴BD=OD．EC=OE。
    又∵DE=OD+DE
    ∴DE=BD+EC。

  • 第10题：

    对于航行于A、B两级航区的船，储备浮力在数值上的关系是（）

    • A、A≤B
    • B、A≥B
    • C、A＝B
    • D、无确定关系

    正确答案:B

  • 第11题：

    若正方形ABCD的边长为4，E为BC边上一点，BE=3，M为线段AE上的一点，射线BM交正方形的一边于点F，且BF=AE，则BM的长为5/2或12/5。


    正确答案:错误

  • 第12题：

    判断题
    若正方形ABCD的边长为4，E为BC边上一点，BE=3，M为线段AE上的一点，射线BM交正方形的一边于点F，且BF=AE，则BM的长为5/2或12/5。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第13题：

    如图：已知圆0，点P在圆外，D，E在圆上，PE交圆于C，PD与圆相切，G为CE上一点且满足PG=PD,连接DG并延长交圆于A，作弦AB⊥EP，垂足为F。

    (1)求证：AB为圆的直径；
    (2)若AC=BD，AB=5，求弦DE的长。


    答案：
    解析：
    (1)证明：∵PG=PD,∴∠PGD=∠PDG，又∵∠AGF=∠PGD，∠PDG=∠ABD，∴∠AGF=∠ABD，∴∠ADB=∠AFP=90°，∴AB为圆的直径。

  • 第14题：

    如右图所示，梯形ABCD的对角线AC⊥BD,其中AD＝1/2,BC＝3,AC＝14/5 ,BD＝2.1.问梯形ABCD的高AE的值是：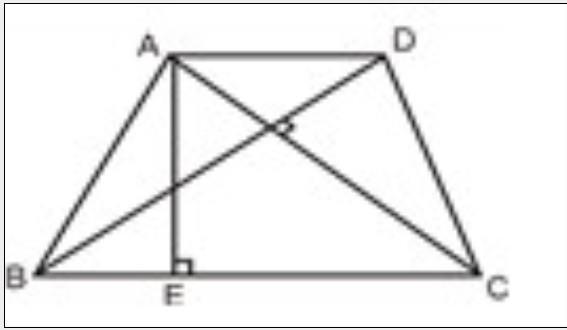

    　
    　

    A. 43/24
    B. 1.72
    C. 42/25
    D. 1.81

    答案：C
    解析：
    解题指导： C。

  • 第15题：

    在边长为1的正方形ABCD中，AC与BD相交于O，以A、B、C、D分别为圆心，以对角线长的一半为半径画圆弧与正方形的边相交，如图，则图中阴影部分的面积为多少?(π=3．14)


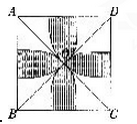    A.0．43
    B.0．57
    C.0．64
    D.0．71

    答案：C
    解析：

  • 第16题：

    已知正六边形ABCDEF的边长为a，PA为过点A而垂直于正六边形所在平面M的垂线，且PA=a，求：
    (I)点P到AB、BC、CD各边的距离；
    (II)PD与平面M所成的角．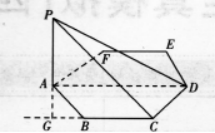


    答案：
    解析：
    (I)如图所示，
    24题答案图
    ∵PA上平面M，∴PA上BC，
    ∴点P到AB的距离为a．过A作BC的垂线交CB的延长线于G，连结PG，
    ∴BC上平面APG，即PG⊥AB，


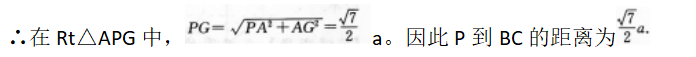
    ∵PA上平面M，
    ∴AC是PC在平面M上的射影，
    又∵AD是正六边形ABCDEF外接圆的直径，
    ∴∠ACD=90o．
    因此AC⊥CD，所以CD⊥平面ACP，即PC是P到CD的距离，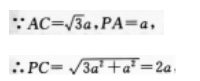

    因此P到CD的距离为2a．
    (Ⅱ)设PD与DA所夹的角为口，在Rt△PAD中，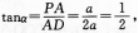

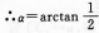    (VI)为PD与平面M所夹的角．

  • 第17题：

    如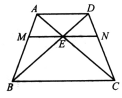，梯形ABCD的上底与下底分别为5，7，E为AC与BD的交点，MN过点E且平行于AD．则MN=


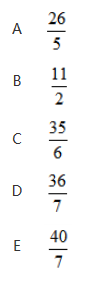    答案：C
    解析：

  • 第18题：

    如右图所示，在△ABC：中，D为AC的中点，E在BC上，且 BE ： EC=1 ： 2，AE与BD交于F。则△BEF与四边形EFDC 的面积之比为（ ）。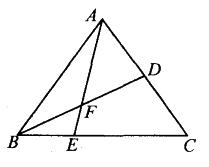

    A. 1 : 3 B. 1 ： 4
    C. 1 ： 5 D. 1 ： 6


    答案：C
    解析：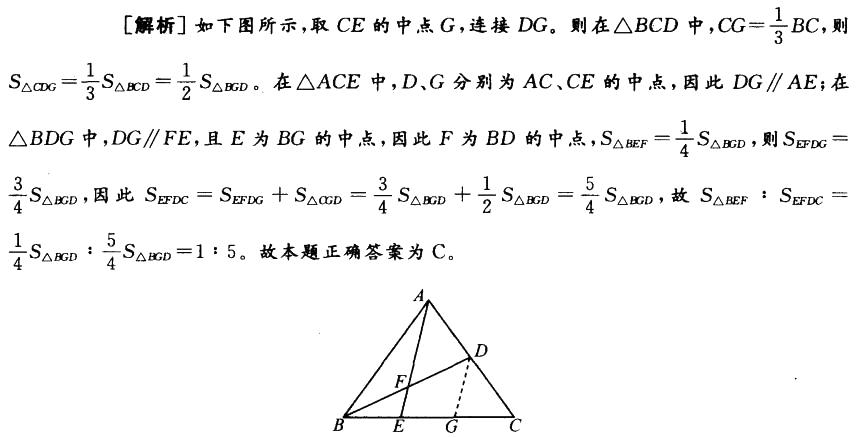

  • 第19题：

    已知△ABC的三边长AC＝3，BC＝4，AB＝5，P为AB边上任意一点，则CP→ (BA→－BC→)的最大值为(　　)

    A、8
    B、9
    C、12
    D、15

    答案：B
    解析：

  • 第20题：

    如图，在一张矩形纸片ABCD中，AB=4，BC=8。点E，F分别在AD，BC上，将纸片ABCD沿直线EF折叠，点C落在AD上的一点日处，点D落在G处，有以下四个结论：①四边形CFHE是菱形；②EC平分∠DCH；③线段BF的取值范围为3≤BF≤4；④当点H与点A重合时, 。以上结论中，你认为正确的有( )个。

    A.1
    B.2
    C.3
    D.4

    答案：C
    解析：

  • 第21题：

    已知BD为正方形ABCD对角线，M为BD上不同于B、D的一个动点，以AB为边在ABCD侧边作等边三角形ABE，以BM为边在BD左侧作等边三角形BMF，连接EF、AM、CM，当AM+BM+CM最短时，∠BCM=( )。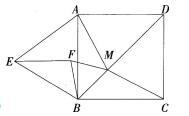

    A.150
    B.450
    C.300
    D.600

    答案：A
    解析：

  • 第22题：

    圆内接四边形ABCD的一组对边AD、BC的延长线相交于户，对角线AC、BD相交于Q点，则图中共有相似三角形（）。

    • A、4对
    • B、2对
    • C、1对
    • D、3对

    正确答案:A

  • 第23题：

    ABCD是边长为L的正方形的四个顶点，若在A、B、C、D四个顶点处分别放置带电量为q的正点电荷，则A、B、C、D四点电荷在正方形对角线交点上产生的合场强的大小为（）。


    正确答案:0

相关内容