从1、2、3、…、n中，任取57个数，使这57个数必有两个数的差为13，则n的最大值为多少？( )A.106 B.107 C.108 D.109

题目
从1、2、3、…、n中，任取57个数，使这57个数必有两个数的差为13，则n的最大值为多少？( )

A.106
B.107
C.108
D.109
相似考题

1.数据个数为偶数,则中数为居于中间位置两个数的平均数,即第(N／2)与第(N／2)＋1位置的两个数据相加除以2。()此题为判断题(对，错)。

2.在一棵二叉树上，度为零的节点的个数为n0，度为2的节点的个数为n2，则n0的值为A．n2+1B．n2-1C．n2D．n2/2

3.从1、2、3、4、5、6、7、8、9、10这10个数字中，任取5个数相加的和与其余5个数相加的和相乘，能得到多少个不同的乘积?（ ）A．13B．14C． 18D． 20

4.已知无穷数集X服从正态分布N(4，25)，现从X中任取10000个数作为样本a，则样本口的标准差为（ ）。A．2B．4C．5D．25

更多“从1、2、3、…、n中，任取57个数，使这57个数必有两个数的差为13，则n的最大值为多少？( )”相关问题

  • 第1题：

    从1,2,…,10这十个自然数中任取三个数，则这三个数中最大的为3的概率是1/120。()


    正确答案:对

  • 第2题：

    在一棵二叉树中,度为零的结点的个数为n0,度为2的结点的个数为n2,则有n0=()

    A、n2

    B、n2+1

    C、n2-1

    D、n2+2


    参考答案：B

  • 第3题：

    有若干个数，第一个数记为a1，第二个数记为a2，…，第n个数记为an。若a1=1/2，从第二个数起，每个数都等于“1与它前面那个数的差的倒数”。试计算：a2=______，a3=____，a4=_____，a5=______。这排数有什么规律吗？由你发现的规律，请计算a2004是多少？


    正确答案：
    a2=2，a3=-1，a4=1/2，a5=2。这排数的规律是:1/2,2,-1循环. a2004=-1

  • 第4题：

    在一棵二叉树上，度为零的接点的个数为N0，度为2的结点的个数为N2，则N0＝

    A．N2+1

    B．N2

    C．N2-1

    D．N2/2


    正确答案：A
    解析：二叉树的基本性质3：设二叉树叶数为N0，度为2的结点数为N2，则N0＝N2+1。一棵树深度为K且有2k-1个结点的二叉树，当且仅当他的深度为K的满二叉树中编号从1到n的结点一一对应时，才是一棵完全的二叉树。度为零的结点即为二叉树的叶子，所以根据二叉树的基本性质3。可以知道答案为N0＝N2+1。

  • 第5题：

    从1、2、3、4、5、6、7、8、9、10这10个数中，任取5个数相加的和与其余5个数相加的和相乘，能得到多少个不l司的乘积？（ ）

    A．13

    B．14

    C．18

    D．20


    正确答案：A
    从整体考虑分两组，和不变：1+2+3+4+5+6+7+8+9+10=55。从极端考虑分成最小和最大的两组为(1+2+3+4+5)+(6+7+8+9+10)=15+40=55，最接近的两组为27+28，所以共有27-15+1=13个不同的积。

  • 第6题：

    从1，2，3，4，5，6，7这七个数字中任取两个奇数和两个偶数，组成没有重复数字的四位数，其中奇数的个数为

    (A)432 (B)288 (C) 216 (D)108


    正确答案：C

  • 第7题：

    从0到9这10个数中任取一个数并且记下它的值，放回，再取一个数也记下它的值。当 两个值的和为8时，出现5的概率是多少？


    答案：C
    解析：
    两个数值的和为8,则可能的情况有0+8、1+7、2+6、3+5、4+4、5+3、6+2、7+1、8+0这9种 情况，其中出现5的有2种情况。因此所求概率为2/9

  • 第8题：

    从1、2、3、4、5这五个数字中等可能地、有放回地接连抽取两个数字，则这两个数字不相同的概率为()



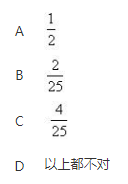    答案：D
    解析：

  • 第9题：

    对任何一棵二叉树T，如果其终端结点的个数为n0，度为2的结点个数为n2，则（）。

    • A、n0=n2-1
    • B、n0=n2
    • C、n0=n2+1
    • D、没有规律

    正确答案:C

  • 第10题：

    如果从1，2，…，10这十个自然数中任取三个数，则这三个数中最大的为3的概率是1/120


    正确答案:正确

  • 第11题：

    问答题
    35.从1，2．3，4，5中任取3个数字，则这3个数字中不含1的概率为

    正确答案：
    解析：

  • 第12题：

    填空题
    在一棵二叉树中，度为0的结点的个数为n0，度为2的结点的个数为n2，则：n0=（）

    正确答案： n2+1
    解析： 暂无解析

  • 第13题：

    从n个数字中有返回地任取r个数(r <= n,且n个数字互不相同),则取到的r个数字中有重复数字的概率为( )。


    参考答案：

  • 第14题：

    在长为n的顺序表中删除一个数据元素,平均需移动()个数据元素。

    A、n

    B、n-1

    C、n/2

    D、(n-1)/2


    正确答案：D

  • 第15题：

    从1，2，3，……，50这五十个数中，取出若干个数，使其中任意两个数的和都不能被7整除，则最多能取多少个数( )。

    A. 21    B. 22C. 23   D. 29


    从0开始，每7个数一组（0——6，7——13，......，42——48，共七组）中，最多可以选4个数（分别是除7余0，1，2，3的数）
    所以，它们之中可以选7*4＝28个数。
    另外：0不包含在其中，要减去1个数；49和50两个数除7的余数分别是0和1，也要计算上，再加2个数。
    故，最多共可取28－1+2＝29个数

  • 第16题：

    从l、2、3、4、5、6、7、8、9、10这l0个数字中， 任取5个数相加的和与其余5个数相加的和相乘，能得到多少个不同的乘积?( )

    A 1 3

    B．1 4

    C．18

    D．20


    正确答案：A
    15．A【解析】从整体考虑， 分两组和不变：1+2+3+4+5+6+7+8+9+10=55。从极端考虑分成最小和最大的两组为(1+2+3+4+5)+(6+7+8+9+10)=15+40=55， 最接近的两组为27+28，所以共有27—15+1=13个不同的积。

  • 第17题：

    从0，1，2，3，4，5这六个数字中任取两个奇数和两个偶数，组成没有重复数字的四位数的个数为

    (A)300 (B)216 (C) 180 (D)162


    正确答案：C

  • 第18题：

    从1、2、3、4中任取3个数组成没有重复的三位数的偶数，取法种数为（）。

    A.13
    B.12
    C.10
    D.11

    答案：B
    解析：
    题干要求组成没有重复数字的三位数的偶数，只有尾数是2或4两种情况。当尾数是2时，有2x3=6(种）；当尾数是4时，有2x3=6(种），所以共有6+6=12(种），故本题答案为B。

  • 第19题：

    从2、3、5三个数中，任取两个数，可组成( )个真分数．


    答案：B
    解析：
    【考情点拨】本题主要考查的知识点为组合数． 【应试指导】从2、3、5中任取两个数，大数做分母，小数做分子，两个数组成的分数是分数形式只有一种，所以所求真分数的个数为3种

  • 第20题：

    完全二叉树的结点个数为4*N+3，则它的叶结点个数为（）。

    • A、2*N
    • B、2*N-1
    • C、2*N+1
    • D、2*N-2
    • E、2*N+2

    正确答案:E

  • 第21题：

    在一棵二叉树中，度为0的结点的个数为n0，度为2的结点的个数为n2，则：n0=（）


    正确答案:n2+1

  • 第22题：

    从数字1，2，…，10中有放回地任取4个数字，则数字10恰好出现两次的概率为（）


    正确答案:0.0486

  • 第23题：

    单选题
    完全二叉树的结点个数为4*N+3，则它的叶结点个数为（）。
    A

    2*N

    B

    2*N-1

    C

    2*N+1

    D

    2*N-2

    E

    2*N+2


    正确答案： D
    解析： 暂无解析

相关内容