从1、2、3、4、5、6、7、8、9、10这10个数字中,任取5个数相加的和与其余5个数相加的和相乘,能得到多少个不同的乘积?( )A.13B.14C. 18D. 20
题目
从1、2、3、4、5、6、7、8、9、10这10个数字中,任取5个数相加的和与其余5个数相加的和相乘,能得到多少个不同的乘积?( )
A.13
B.14
C. 18
D. 20
相似考题
更多“从1、2、3、4、5、6、7、8、9、10这10个数字中,任取5个数相加的和与其余5个数相加的和相乘,能得到多少个不同的乘积?( )A.13B.14C. 18D. 20”相关问题
-
第1题:
从l、2、3、4、5、6、7、8、9、10这l0个数字中, 任取5个数相加的和与其余5个数相加的和相乘,能得到多少个不同的乘积?( )
A 1 3
B.1 4
C.18
D.20
正确答案:A
15.A【解析】从整体考虑, 分两组和不变:1+2+3+4+5+6+7+8+9+10=55。从极端考虑分成最小和最大的两组为(1+2+3+4+5)+(6+7+8+9+10)=15+40=55, 最接近的两组为27+28,所以共有27—15+1=13个不同的积。 -
第2题:
从0、3、5、7、11五个数中任取两个数相乘,可以得到( )个不相等的积。
A.5
B.4
C.6
D.7
正确答案:D
因为0和任何数相乘都等于0,所以其只算是一种乘积,C(2/4)=6,所以可以得到7个不同的乘积。 -
第3题:
从1、2、3、4、5、6、7、8、9、10这10个数中,任取5个数相加的和与其余5个数相加的和相乘,能得到多少个不同的乘积?( )
A.13
B.14
C.18
D.20
正确答案:A
A【解析】从整体考虑分两组,和不变:1+2+3+4+5+6+7+8+9+10=55,从极端考虑分成最小和最大的两组为(1+2+3+4+5)+(6+7+8+9+10)=15+40=55,最接近的两组为27+28,所以共有27-15+1=13个不同的积。
-
第4题:
从1,2,3,4,5,6,7这七个数字中任取两个奇数和两个偶数,组成没有重复数字的四位数,其中奇数的个数为
(A)432 (B)288 (C) 216 (D)108
正确答案:C
-
第5题:
A、B、C、D、E是5个不同的整数,两两相加的和共有8个不同的数值,分别是17、25、28、31、34、39、42、45,则这5个数中能被6整除的有几个?
A.0
B.1
C.2
D.3答案:C解析:.[解析] 不妨设A<B<C<D<E,则必有A+B=17,A+C=25,C+E=42,D+E=45。两两相加,本应有 个和值(计入和值相等的情况),而只得到8个不同和值。将10个和值加总,必为4的倍数;将8个和值加总,得261(除以4余1)。易知,重复的2个和值必在中间4个数中,即为28、31、34、39中的两数,且这两数之和除以4的余数为3。易知这两个数为28、39或者28、31。由28必为重复值,可分析知B+C=A+D=28,结合前面所列方程,可求出A=7,B=10,C=18,D=21,E=24。本题选C。 -
第6题:
从0,2,4,6中取出3个数字,从1,3,5,7中取出两个数字,共能组成多少个没有重复数字且大于65000的五位数答案:解析:根据约束条件“大于65000的五位数”可知这样的五位数只有 7××××、65×××、67×××三种类型.
(1)能组成7××××型的五位数的个数是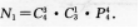
(2)能组成65×××型的五位数的个数是
(3)能组成67×××型的五位数的个数是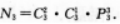
故所求的五位数的个数为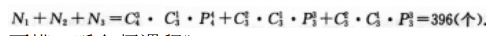
-
第7题:
A、
B、
C、
D、E是5个不同的整数,两两相加的和共有8个不同的数值,分别是17、25、28、31、34、39、42、45,则这5个数中能被6整除的有几个?
A.0 B.1 C.2 D.3答案:C解析:
-
第8题:
从1、2、3、4、5、6、7、8、9这几个数字中选择3个数字,使它们的乘积能够被9整除,问共 有多少种不同的方法?
a.34 b.36 c.27 d.25答案:A解析:9=lx9=3x3。1~9中的三个自然数的乘积能被9整除,可以分为两种情况:(1)这三个数 字中有9,则另外两个数字可在剩下8个数中任意选择,有C82=28种;(2)这三个数字中没有9,则这三个数字中 必有3和6,第三个数字有9-3=6种选择。由加法原理可知,共有28+6=34种选择。 -
第9题:
单选题从1,2,…,9共九个数字中任取一个数字,取出数字为偶数的概率为( ).A0
B1
C5/9
D4/9
正确答案: B解析: 9个数。偶数的个数是4个
-
第10题:
A、B、C、D、E是5个不同的整数,两两相加的和共有8个不同的数值,分别是l7、25、28、31、34、39、42、45,则这5个数中能被6整除的有几个?( )
A.0
B.1
C.2
D.3
正确答案:C
-
第11题:
从1、2、3、4、5、6、7、8、9、10这10个数中,任取5个数相加的和与其余5个数相加的和相乘,能得到多少个不l司的乘积?( )
A.13
B.14
C.18
D.20
正确答案:A
从整体考虑分两组,和不变:1+2+3+4+5+6+7+8+9+10=55。从极端考虑分成最小和最大的两组为(1+2+3+4+5)+(6+7+8+9+10)=15+40=55,最接近的两组为27+28,所以共有27-15+1=13个不同的积。 -
第12题:
A、B、C、D、E 是5 个不同的整数,两两相加的和共有8 个不同的数值,分别是 17、25、28、31、34、39、42、45,则这 5 个数中能被 6 整除的有几个?
A.0
B.1
C.2
D.3
正确答案:C
14.C. [解析] 不妨设ABCDE,则必有A+B=17, A+C=25, C+E=42,D+E=45。两两相加,本应有 个和值(计入和值相等的情况),而只得到 8 个不同和值。将 10 个和值加总,必为 4 的倍数;将 8 个和值加总,得 261(除以 4 余 1)。易知,重复的 2 个和值必在中间4 个数中,即为 28、31、34、39 中的两数,且这两数之和除以4 的余数为3。易知这两个数为 28、 39 或者 28、 31。由 28 必为重复值,可分析知 B+C=A+D=28,结合前面所列方程,可求出 A=7,B=10,C=18,D=21,E=24。本题选 C。 -
第13题:
1、2、3、4、5、6、7、8、9这九个数字各用一次,组成三个能被9整除的三位数,这三个数的和最大是:A.2007
B.2394
C.2448
D.2556答案:C解析:第一步,本题考查多位数问题。
第二步,1—9这九个数字各用一次,先将1—9加和为45,组成三个能被9整除的三位数,可知每个三位数各位数字加和均为9的倍数,则三个三位数各位数字加和分别为9、18、18。
第三步,要使这三个数的和最大,则每个三位数百位上的数字应尽量大,先考虑和为9的三位数,百位最大为6,这个三位数是621,剩余两个三位数最大分别为954和873,则954+873+621=2448(可用尾数法,尾数为8)。 -
第14题:
从1、2、3、4、5、6、7、8、9这几个数字中选择3个数字,使它们的乘积能够被9整除,问共有多少种不同的方法?( )A.34
B.36
C.27
D.25答案:A解析:9=1×9=3×3。1~9中的三个自然数的乘积能被9整除,可以分为两种情况:(1)这三个数字中有9,则另外两个数字可在剩下8个数中任意选择,有C28=28种;(2)这三个数字中没有9,则这三个数字中必有3和6.第三个数字有9-3=6种选择。由加法原理可知,共有28+6=34种选择。 -
第15题:
从3、5、7、11四个数中任取两个数相乘,可以得到多少个不相等的积:
A 5
B 4
C 6
D 7答案:C解析:
-
第16题:
从1,2,3,4,5,6,7中任取2个数字,分别作为一个分数的分子和分母,则在所得分数中不相同的最简真分数一共有多少个?A.14
B.17
C.18
D.21答案:B解析:根据题意,当分母为2时,分子可为1;分母为3时,分子可为1、2;分母为4时,分子可为1、3;分母为5时,分子可为1、2、3、4;分母为6时,分子可为1、5;分母为7时,分子可为1、2、3、4、5、6。因此,满足条件的最简真分数共有1+2+2+4+2+6=17个。 -
第17题:
在0,1,2,3,4,5,6,7,8,9中随机抽取一个数字,设A为抽取的数字≤5,则P(A)=()。
正确答案:0.6 -
第18题:
问答题35.从1,2.3,4,5中任取3个数字,则这3个数字中不含1的概率为正确答案:解析:
