物体作定轴转动的运动方程为φ=4t-3t2(φ以rad计,t以s计)。此物体内,转动半径r=0. 5m的一点,在t0=0时的速度和法向加速度的大小分别为: A.2m/s,8m/s2 B.3m/s,3m/s2 C. 2m/s,8. 54m/s2 D.0,8m/s2
题目
B.3m/s,3m/s2
C. 2m/s,8. 54m/s2
D.0,8m/s2
相似考题
更多“物体作定轴转动的运动方程为φ=4t-3t2(φ以rad计,t以s计)。此物体内,转动半径r=0. 5m的一点,在t0=0时的速度和法向加速度的大小分别为: ”相关问题
-
第1题:
小车沿水平方向向右做加速运动,其加速度a0=49.2cm/s2,在小车上有一轮绕O轴转动,转动规律为φ=t2(t以秒计,φ以弧度计)。当t=1s时.轮缘上点A的位置如图所示。如轮的半径r=20cm,求此时点A的绝对加速度aA为( )cm/s2。
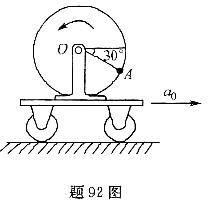
A.24.7
B.43.5
C.68.2
D.74.6答案:D解析:牵连运动为平动 -
第2题:
物体作定轴转动的运动方程为φ=4t-3t2(φ以rad计,t以s计)此物体内,转动半径r=0.5m的一点在to=0时的速度和法向加速度的大小为()。A.2 m/s,8 m/s2
B.3 m/s,3 m/s2
C.2 m/s,8.54m/s2
D.0.8 m/s2答案:A解析:提示 根据转动刚体内一点的速度和加速度公式:v=rw,an=rw2,且w=φ。@## -
第3题:
作定轴转动的刚体,体内任一点法向加速度的方向指向()。
- A、外法线
- B、转轴
- C、该点切向
- D、任一方向
正确答案:B -
第4题:
一质点P沿半径R的圆周作匀速率运动,运动一周所用时间为T,则质点切向加速度的大小为();法向加速度的大小为()
正确答案:0;4π2R/T2 -
第5题:
刚体以角速度ω,角加速度ε绕定轴转动则在其转动半径为r处的线速度v=(),切线加速度at=(),法向加速度an=()。
正确答案:ωr;εr;ω2r -
第6题:
由定轴转动刚体上某一点的法向加速度的大小,即可知道刚体转动角速度的大小和方向。
正确答案:错误 -
第7题:
如果知道定轴转动刚体上某一点的法向加速度,就可确定刚体转动角速度的大小和转向。
正确答案:错误 -
第8题:
质点运动方程x=t2+2t-3,x以米计,t以秒计,则该质点2秒末的速度v=();加速度a=()。
正确答案:6m/s;2m/s2 -
第9题:
填空题刚体以角速度ω,角加速度ε绕定轴转动则在其转动半径为r处的线速度v=(),切线加速度at=(),法向加速度an=()。正确答案: ωr,εr,ω2r解析: 暂无解析 -
第10题:
单选题(2012)物体作定轴转动的运动方程为φ=4t-3t2(φ以rad计,t以s计)此物体内,转动半径r=0.5m的一点,在t0=0时的速度和法向加速度的大小分别为:()A2m/s,8m/s2
B3m/s,3m/s2
C2m/s,8.54m/s2
D0,8m/s2
正确答案: A解析: 暂无解析 -
第11题:
单选题物体作定轴转动的运动方程为φ=4t-3t2(φ以rad计,t以s计)。此物体内,转动半径r=0.5m的一点,在t0=0时的速度和法向加速度的大小为( )。[2012年真题]A2m/s,8m/s2
B3m/s,3m/s2
C2m/s,8.54m/s2
D0,8m/s2
正确答案: D解析:
物体转动的角速度为:ω=dφ/dt=4-6t,则当t0=0时,ω0=4(rad/s)。故所求点的速度v0=rω0=0.5×4=2m/s,加速度a0=rω02=0.5×42=8m/s2。 -
第12题:
判断题如果知道定轴转动刚体上某一点的法向加速度,就可确定刚体转动角速度的大小和转向。A对
B错
正确答案: 错解析: 暂无解析 -
第13题:
已知质点沿半径为40cm的圆周运动,其运动规律为s=20t(s以cm计,t以s计)。若t=1s,则点的速度与加速度的大小为: 答案:B解析:
答案:B解析:
-
第14题:
已知点沿半径为40cm的圆周运动,其运动规律为s=20t(s以厘米计,t以秒计)。 若t=ls,则点的速度与加速度的大小为( )。 答案:B解析:提示:点的速度、切向加速度和法向加速度分别为:
答案:B解析:提示:点的速度、切向加速度和法向加速度分别为: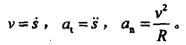
-
第15题:
点作直线运动,其运动方程为x=27t-t3,式中x以m计,t以s计。则点在t=0到t=7s时间间隔内走过的路程为()m。
正确答案:262 -
第16题:
作定轴转动的刚体,体内任一点的法向加速度其大小等于与转动半径()
- A、反比
- B、正比
- C、无关
- D、指数关系
正确答案:B -
第17题:
已知刚体作匀速定轴转动,刚体上某一点的速度为16m/s,转动半径为0.5m,则角速度为()。
- A、16rad/s
- B、8rad/s
- C、4rad/s
- D、32rad/s
正确答案:D -
第18题:
点M在曲线AOB上运动。曲线由AO、OB两段圆弧组成。AO段曲率半径R1=18m,OB段曲率半径R2=24m,取两圆弧交接点O为原点,并规定正负方向如图示。已知点M的运动方程为s=3+4t-t2(t以秒计,s以米计),则t=5秒时点M的加速度大小为()。
- A、1.5m/s2
- B、2m/s2
- C、2m/s2
- D、4m/s2
正确答案:C -
第19题:
作定轴转动的刚体上各点的法向加速度,既可写为an=v2/R,这表示法向加速度的大小与刚体上各点到转轴的距离R成反比;也可以写为an=ω2R,这表示法向加速度的大小与刚体上各点到转轴的距离R成正比。这两者是否有矛盾?为什么?
正确答案:没有矛盾。根据公式an=v2/R,说法向加速度的大小与刚体上各点到转轴的距离R成反比,是有条件的,这个条件就是保持v不变;根据公式an=ω2R,说法向加速度的大小与刚体上各点到转轴的距离R成正比,也是有条件的,条件就是保持ω不变。 -
第20题:
半径为30cm的飞轮,从静止开始以0.5rad·s-2的匀角加速转动,则飞轮边缘上一点在飞轮转过240˚时的切向加速度at=(),法向加速度an=()。
正确答案:0.15;1.256 -
第21题:
单选题物体做定轴转动的运动方程为φ=4t-3t2,则此物体转动半径r=0.5m的一点,在t=1s的速度和切向加速度为( )。[2019年真题]A2m/s,20m/s2
B-1m/s,-3m/s2
C2m/s,8.54m/s2
D0m/s,20.2m/s2
正确答案: A解析:
某点的速度与角速度关系为:v=ωr。其中,角速度ω=dφ/dt=4-6t。因此,在t=1s时,ω=-2rad/s,则v=-2×0.5=-1m/s。某点切向加速度与角加速度关系为:aτ=αr。其中,角加速度α=dω/dt=-6rad/s2。因此,在t=1s时,切向加速度aτ=-6×0.5=-3m/s2。 -
第22题:
单选题(2010)已知质点沿半径为40cm的圆周运动,其运动规律为s=20t(s以cm计,t以s计)。若t=1s,则点的速度与加速度的大小为:()A20cm/s;10cm/s2
B20cm/s;10cm/s2
C40cm/s;20cm/s2
D40cm/S;10cm/s2
正确答案: D解析: 暂无解析 -
第23题:
单选题点沿圆周作匀速运动,速度大小等于5m/s,圆周的半径为10cm。其法向加速度等于()。A0.5
B5
C50
D250
正确答案: D解析: 暂无解析
