某工程队承担了A，B两个工程任务，A工程的工作是B工程的两倍，施工过程如下：第一阶段15天，全体人员投入到A工程中，完成了A工程的部分工作量；第二阶段20天，一半人员投入到A工程中，一半人员投入到B工程中，完成了A工程的剩余工作量和B工程的部分工作量；第三阶段10天，10个人投入到B工程中，完成了B工程的剩余工程量，每个人的工作效率相等，该工程队共有多少人？A.64B.58C.48D.40

题目

某工程队承担了A，B两个工程任务，A工程的工作是B工程的两倍，施工过程如下：第一阶段15天，全体人员投入到A工程中，完成了A工程的部分工作量；第二阶段20天，一半人员投入到A工程中，一半人员投入到B工程中，完成了A工程的剩余工作量和B工程的部分工作量；第三阶段10天，10个人投入到B工程中，完成了B工程的剩余工程量，每个人的工作效率相等，该工程队共有多少人？

A.64

B.58

C.48

D.40

相似考题

1.两个工程队修一公路，甲工程队10天修了45公里，乙工程队以比甲工程队快两倍的速度修了15天，问乙工程队修了多少公里?（ ）A．102.5公里B．202.5公里C．135公里D．235公里

2.甲乙两个工程队承担了精准扶贫村公路的修筑任务，先是甲工程队单独修了10天，完成了总工程的四分之一，接着乙工程队加入合作，完成剩余工程。在第14天完成到总工程的一半，则按照这种进度完成全部工程所用的天数比由甲单独完成这项工程少用的天数是 A.12天 B.20天 C.18天 D.16天

3. 有甲乙两个工程队负责某小区主干道维修及墙面粉刷。主干道维修，如果两个工程队合作，30天完成，若乙工程队单独进行，105天完成；粉刷墙面，若两个工程队合作，28 天完成，若甲工程队单独做，140 天完成。如果两项工作两个工程队共同分工合作，最少需要多少天？A.34 B.35 C.40 D.41

4.某工程队承担了A、B两个工程任务,A工程的工作是B工程的两倍,施工过程如下:第一阶段15天,全体人员投入到A工程中,完成了A工程的部分工作量;第二阶段20天,一半人员投入到A工程中,一半人员投入到B工程中,完成了A工程的剩余工作量和B工程的部分工作量;第三阶段10天,10个人投入到B工程中,完成了B工程的剩余工程量,每个人的工作效率相等,该工程队共有多少人？A.64 B.58 C.48 D.40

更多“某工程队承担了A,B两个工程任务,A工程的工作是B工程的两倍,施工过程如下:第一阶段15天,全体 ”相关问题

  • 第1题：

    有甲乙两个工程队负责某小区主干道维修及墙面粉刷。主干道维修，如果两个工程队合作，30天完成，若乙工程队单独进行，105天完成；粉刷墙面，若两个工程队合作，28天完成，若甲工程队单独做，140天完成。如果两项工作两个工程队共同分工合作，最少需要多少天?

    A.34
    B.35
    C.40
    D.41

    答案：C
    解析：
    第一步，本题考查工程问题，属于时间类，用赋值法解题。
    第二步，赋值维修主干道的总量为1050（30和105的公倍数），则甲乙合作的效率为1050÷30＝35，乙的效率为1050÷105＝10，则甲的效率为35－10=25；赋值墙面粉刷的总量为140（28和140的公倍数），则甲乙合作的效率为140÷28＝5，甲的效率为140÷140＝1，则乙的效率为5－1=4。可知，甲维修主干道的效率比乙高，乙粉刷墙面的效率比甲高。
    第三步，问项目最少需要多少天，则甲和乙做自己效率更高的项目。所以由甲维修主干道，乙负责墙面粉刷。乙粉刷墙面需要140÷4=35（天），而甲35天可以维修道路的工作量为35×25＝875。
    第四步，维修道路剩余工作量为1050－875＝175，剩余工作量由甲乙合作完成，还需要175÷35＝5（天）。故一共需要35＋5＝40（天）。

  • 第2题：

    甲、乙两个工程队合作完成某工程需36天，若甲工程队先做10天，剩下的工程再由两队合作30天完成。问乙工程队的工作效率是甲工程队的：


    答案：A
    解析：
    第一步，本题考查工程问题，属于时间类。
    第二步，设甲、乙工程队的工作效率分别为x、y，根据题意可列出等式：36（x＋y）＝10x＋30（x＋y），化简得y∶x＝2∶3。
    因此，选择A选项。

  • 第3题：

    甲、乙两个工程队合作完成某工程需36天，若甲工程队先做10天，剩下的工程再由两队合作30天完成。问乙工程队的工作效率是甲工程队的：

    A.2/3
    B.4/5
    C.3/4
    D.1/2

    答案：A
    解析：
    本题属于工程问题。
    设甲工程队的效率为x，乙工程队的效率为y。根据工程总量不变可列式：36×（x+y）=10x+30×（x+y），化简得2x=3y，即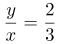}，即乙工程队的工作效率是甲工程队的{图1。
    因此，选择A选项。

  • 第4题：

    甲、乙两个工程队修公路，甲工程队修500米后由乙工程队来修，由以往资料显示乙工程队的效率是甲工程队的两倍，乙工程队修600米的时间比甲工程队修500米的时间少20天，甲工程队的工作效率为（　　）米／天。

    A.20
    B.15
    C.10
    D.25

    答案：C
    解析：
    根据甲、乙效率比可知，相同时间，乙修600米，甲修300米。即甲修300米所用时间比其修500米所用时间少20天，故甲修200米用20天，每天修200÷20=10(米)。

  • 第5题：

    某工程由甲、乙两工程队合作需要10天完成，乙、丙两个工程队合作需要7天完成，甲、乙、丙三个工程队合作需要5天完成。现甲、乙、丙三个工程队同时工作，2天后，乙工程队因有其他任务撤离该工程，问甲、丙两个工程队还需多少天能完成该工程？（ ）

    A.3
    B.4
    C.5
    D.6

    答案：B
    解析：
    设工程总量为70，则甲的效率+乙的效率=70÷10=7，乙的效率+丙的效率=70÷7=10,甲的效率+乙的效率+丙的效率=70÷5=14，则甲的效率=14－10=4，丙的效率=14－7=7。甲、乙、丙前两天共同完成的工作量=14×2=28，剩余工作量=70－28=42。甲、丙同时完成剩余工作量需要天数=42÷(4+7)≈3.8(天），故答案为B。

相关内容