用八个同样大小的等腰直角三角形拼成一个正方形，若三角形的面积为2平方厘米，那么正方形的周长是( ) 。A．8B．16C．20D．32
题目
用八个同样大小的等腰直角三角形拼成一个正方形，若三角形的面积为2平方厘米，那么正方形的周长是( ) 。
A．8
B．16
C．20
D．32
相似考题
更多“用八个同样大小的等腰直角三角形拼成一个正方形,若三角形的面积为2平方厘米,那么正方形的周长是( ”相关问题
-
第1题：
已知有6个大小相同，标号分别为1～6的正方形。若旋转后正方形编号相同算同一种拼法，那么要将这些木块拼成一个大长方形，有多少种不同的拼法？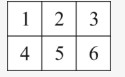
A.360
B.540
C.720
D.900答案：C解析：第一步，本题考查排列组合问题。
第二步，如下图所示，6个正方形组成一个长方形可以分为两种情况。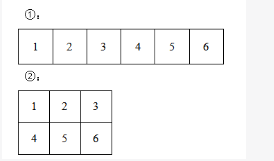
-
第2题：
在大小相等的两个等腰直角三角形中，按不同的方式各内接一个正方形（如图A、B所示）。如果图B中的内接正方形的面积是144，那么图A中的内接正方形的面积是多少？
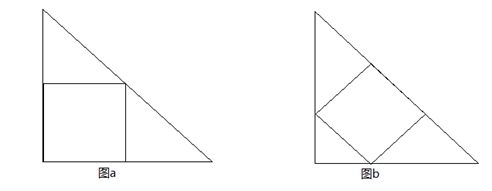A. 225
B. 162
C. 128
D. 98答案：B解析：
-
第3题：
如图所示，大正方形周长比小正方形周长多 80，阴影部分的面积为 880，大正方形面积是：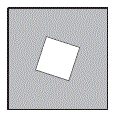
A.144
B.625
C.900
D.1024答案：D解析：大正方形周长比小正方形多80，则边长多20，设小正方形边长为x，大正方形为x+20。（ｘ＋20）2-x2=880，解得x=12。大正方形面积为880+122=1024。 -
第4题：
如图，它是由15个同样大小的正方形组成。如果这个图形的面积是375平方厘米，那么，它的周长是( )。
A. 150
B. 155
C. 160
D. 165答案：C解析：解题指导： 每个正方形的面积为375÷15=25平方厘米，边长为5厘米。周长为5×32=160厘米。故答案为C。 -
第5题：
如图，由四个全等的直角三角形拼成一个大正方形，每个三角形的面积都是1，且两直角边之比大于等于2，则这个大正方形的面积至少是()。
A.4
B.5
C.6
D.7答案：B解析：第一步，本题考查几何问题，属于平面几何类。
第二步，根据图形可知大正方形面积＝4个三角形面积＋小正方形面积＝4＋小正方形面积，小正方形边长＝三角形长直角边－短直角边，那么当三角形两直角边差最小时，可得大正方形面积最小，由于两直角边之比大于等于2，即当两直角边之比等于2时，大正方形面积最小。
第三步，设三角形短直角边为a，则长直角边为2a，三角形的面积为
解得a＝1，所以小正方形的面积为（2a－a）2＝1×1＝1，故大正方形面积至少为4＋1＝5。
因此，选择B选项。