如图.△ABC是一个等腰直角三角形,它与一个正方形叠放在一起,已知AE=EF=FB,⊿EFD的面积是4 cm2,则⊿ABC的面积是________cm2。
题目
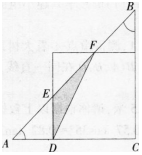
如图.△ABC是一个等腰直角三角形,它与一个正方形叠放在一起,已知AE=EF=FB,⊿EFD的面积是4 cm2,则⊿ABC的面积是________cm2。

相似考题
更多“如图.△ABC是一个等腰直角三角形,它与一个正方形叠放在一起,已知AE=EF=FB,⊿EFD的面积是4 cm2,则⊿ABC的面积是________cm2。 ”相关问题
-
第1题:
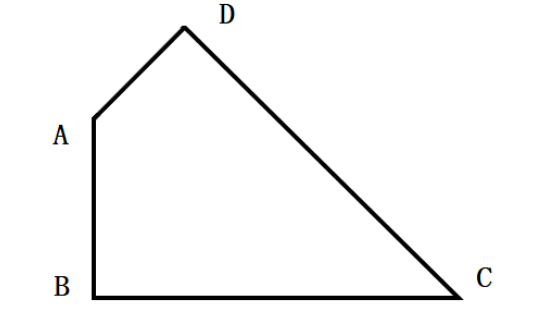
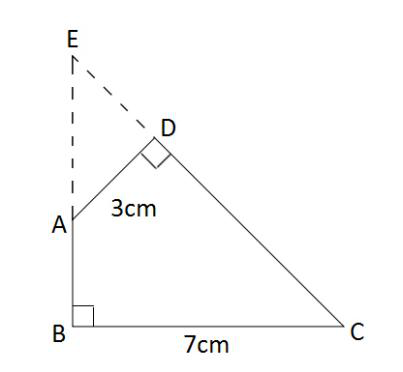
如图,已知一个四边形中边AD长为3cm,边BC长7cm;∠DAB=135°,∠ABC=∠ADC=90°那么这个四边形的面积是( )cm2。
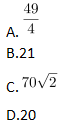 答案:D解析:第一步,本题考查几何问题,用割补平移法解题。
答案:D解析:第一步,本题考查几何问题,用割补平移法解题。
第二步,作BA和CD的延长线交于E,如图所示,得到三角形EBC和ADE。容易知道所求四边形ABCD面积等于△EBC面积减去△ADE面积。由题意∠DAB=135°,∠ABC=∠ADC=90°,可以求得∠DCB=360°-135°-90°×2=45°,且∠BEC=∠EAD=45°,所以△EBC和△ADE都是等腰直角三角形。
第三步,因为AD长3cm,BC长7cm,则BE=BC=7cm,DE=AD=3cm,所以
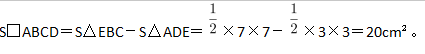
-
第2题:
如图,已知图中四边形两条边的长度和三个角的度数,四边形ABCD的面积是______cm2。 答案:解析:24。解析:延长AD和BC交于点E,则得到两个等腰直角三角形△ABE和△DCE,四边形ABCD
答案:解析:24。解析:延长AD和BC交于点E,则得到两个等腰直角三角形△ABE和△DCE,四边形ABCD
-
第3题:
如右图所示,△ABC是等腰直角三角形,AB=12,AD的长度是CD的2倍,四边形EBCD与△AED的面积之比为3:2,问AE的长度是多少( )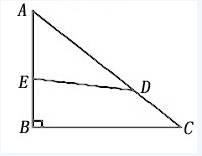
A.6.9 B.7.1 C.7.2 D.7.4答案:C解析:C。由题意可知三角形AED和三角形ABC的面积比为2︰5,AD/AC=2/3,得(0.5AE×AD)/(0.5AB×AC)=2/5,解得AE=7.2。 -
第4题:
下图中正方形的边长为6em,已知正三角形覆盖了正方形1/2的面积,正方形覆盖了正三角形3/4的面积。三角形的面积为( ) cm2。 A.18
A.18
B.20
C.24
D.36答案:C解析:正方形面积为6x6=36,则覆盖面积为36÷2=18,所以三角形面积为18÷3/4-=24. -
第5题:
如图,已知一个四边形中边AD长为3cm,边BC长7cm;∠DAB=135°,∠ABC=∠ADC=90°那么这个四边形的面积是( )。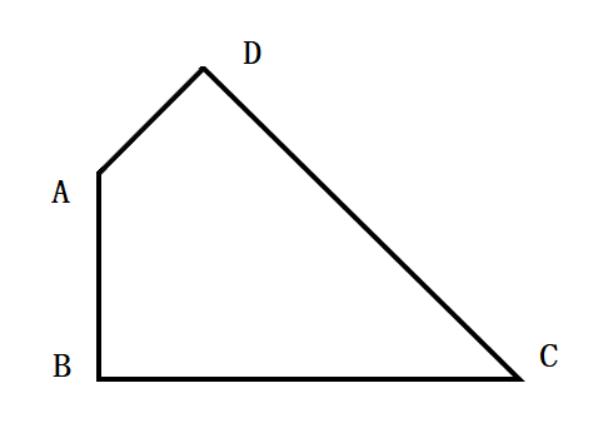
A.49/4
B.21
C.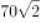
D.20答案:D解析:
-
第6题:
如图,由四个全等的直角三角形拼成一个大正方形,每个三角形的面积都是1,且两直角边之比大于等于2,则这个大正方形的面积至少是()。 A.4
A.4
B.5
C.6
D.7答案:B解析:第一步,本题考查几何问题,属于平面几何类。
第二步,根据图形可知大正方形面积=4个三角形面积+小正方形面积=4+小正方形面积,小正方形边长=三角形长直角边-短直角边,那么当三角形两直角边差最小时,可得大正方形面积最小,由于两直角边之比大于等于2,即当两直角边之比等于2时,大正方形面积最小。
第三步,设三角形短直角边为a,则长直角边为2a,三角形的面积为
解得a=1,所以小正方形的面积为(2a-a)2=1×1=1,故大正方形面积至少为4+1=5。
因此,选择B选项。 -
第7题:
如图所示,ΔABC是直角三角形,四边形和四边形都是正方形,已知4cm,问正方形HFGF的面积是多少?( )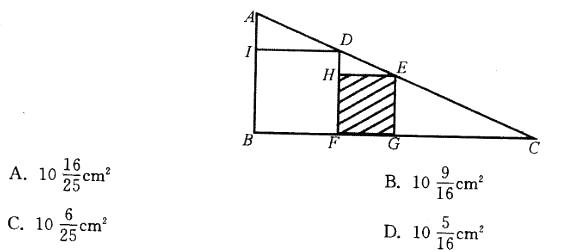 答案:C解析:
答案:C解析:
-
第8题:
已知△ABC和△A'B'C'满足AB:A'B'=AC:AC'=2:3,∠A+∠A'=,则△ABC和△A'B'C'的面积比为( ) 答案:E解析:特值法:假设AB=AC=2,A'B'=A'C'=3,∠A=∠A'=2,S:S'=12*2*2:12*3*3=4:9
答案:E解析:特值法:假设AB=AC=2,A'B'=A'C'=3,∠A=∠A'=2,S:S'=12*2*2:12*3*3=4:9 -
第9题:
如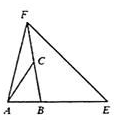 ,已知AE=3AB,BF=2BC。若ΔABC的面积是2,则ΔAEF的面积为A.14
,已知AE=3AB,BF=2BC。若ΔABC的面积是2,则ΔAEF的面积为A.14
B.12
C.10
D.8
E.6答案:B解析:因为是等高三角形,故面积比等于底边比.BF=2BC,.△ABF=2S△ABC=4 AE=3AB,.△AEF=3S△ABF=12故选B -
第10题:
如图所示,ΔABC是直角三角形,四边形和四边形HFGE都是正方形,已知AI=1cm,IB=4cm,问正方形HFGE的面积是多少?( )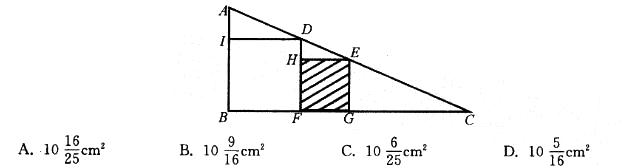 答案:C解析:根据题意,AB = 5cm,ID=BF=4cm,我们利用比例关系“AI : ID = AB : BC”可得 BC=20cm,那么FC=BC-BF=16(cm)。我们假设EG=FG=xcm,那么GC=16-x,再利用比例关系"AB : BC=EG : GC”,得到5 : 20 = x : (16-x),解得x=3. 2,那么正方形HFGE 的面积为x2=
答案:C解析:根据题意,AB = 5cm,ID=BF=4cm,我们利用比例关系“AI : ID = AB : BC”可得 BC=20cm,那么FC=BC-BF=16(cm)。我们假设EG=FG=xcm,那么GC=16-x,再利用比例关系"AB : BC=EG : GC”,得到5 : 20 = x : (16-x),解得x=3. 2,那么正方形HFGE 的面积为x2=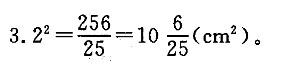
-
第11题:
在△ABC中,若2cosBsinA=sinC,则△ABC的形状一定是()。
- A、等腰直角三角形
- B、直角三角形
- C、等腰三角形
- D、等边三角形
正确答案:C -
第12题:
单选题在△ABC中,若2cosBsinA=sinC,则△ABC的形状一定是()。A等腰直角三角形
B直角三角形
C等腰三角形
D等边三角形
正确答案: B解析: 暂无解析 -
第13题:
数学运算。通过运算,选择最合适的一项。
如图,在△ABC中,已知BD=2DC,EC=2AE,则△BFD与△AEF面积的比值为( )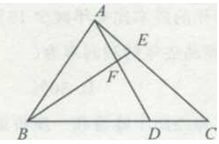 A.4 B.6 C.8 D.9答案:C解析:几何问题。连接CF,因为BD=2DC,EC=2AE,所以设
A.4 B.6 C.8 D.9答案:C解析:几何问题。连接CF,因为BD=2DC,EC=2AE,所以设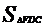 =a,则
=a,则 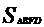 =2a;设
=2a;设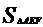 =1,则
=1,则 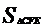 =2。结合图形列方程组得
=2。结合图形列方程组得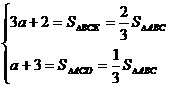 ,两式相除可得a=4。所以
,两式相除可得a=4。所以  ,C项当选。
,C项当选。 -
第14题:
如图所示,△ABC是直角形,四边形IBFD和四边形HFGE都是正方形,已知AI=1cm,IB=4cm,问正方形HFGE的面积是多少( )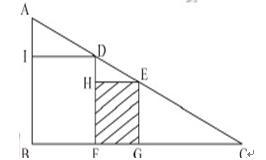
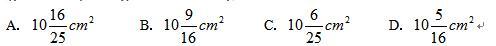 答案:C解析:C。设正方形HFGE的边长为X,由三角形EHD相似于三角形DIA可知,EH/DH=DI/DA,即X/(X-4)=4/1,解得X=16/5,那么正方形面积为X的平方等于10.24。
答案:C解析:C。设正方形HFGE的边长为X,由三角形EHD相似于三角形DIA可知,EH/DH=DI/DA,即X/(X-4)=4/1,解得X=16/5,那么正方形面积为X的平方等于10.24。 -
第15题:
数学运算。在这部分试题中,每道试题呈现一段表述数字关系的文字.要求你迅速、准确地计算出答案。
如图所示,ΔABC是等腰直角三角形,AB=12,AD的长度是CD的2倍,四边形EBCD与ΔAED的面积之比为3:2。问AE的长度是多少?()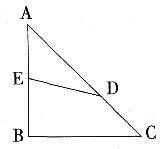
A.6.9
B.7.1
C.7.2
D.7.4答案:C解析:,即
×AE×
×12=
×
×12×12,得AE=7.2。
-
第16题:
如下图所示,已知△ABC的面积为240平方厘米,D是BC的中点,AD的长是AE长的3倍,EF的长是BF长的3倍,那么,△AEF的面积是多少平方厘米?( )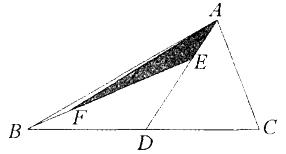 A. 27.5
A. 27.5
B. 40
C. 30
D. 25答案:C解析:若已知两个三角形的高相等,则二者面积之比等于底边之比。本题中D是BC的中点,故
-
第17题:
在大小相等的两个等腰直角三角形中,按不同的方式各内接一个正方形(如图A、B所示)。如果图B中的内接正方形的面积是144,那么图A中的内接正方形的面积是多少?
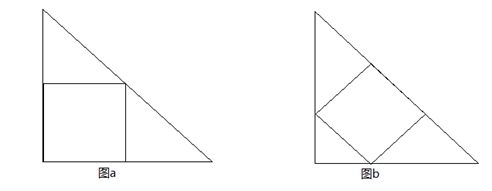 A. 225
A. 225
B. 162
C. 128
D. 98答案:B解析:
-
第18题:
如图,在△ABC中,已知BD=2DC,EC=2AE,则△BFD与△AEF面积的比值为( )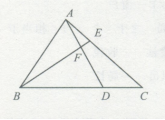 A.4
A.4
B.6
C.8
D.9答案:C解析:C。几何问题。连接CF,因为BD=2DC,EC=2AE,所以设 ,则 ;设 ,则 。结合图形列方程组得 ,两式相除可
得a=4b。所以 ,C项当选。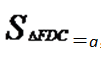
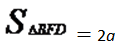

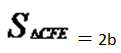

-
第19题:
△ABC中,已知acosA=bcosB,则△ABC是A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰三角形或直角三角形答案:D解析: -
第20题:
两个等腰三角形如图6-12所示叠放在一块,已知BD=6,DC=4,则重合部分的阴影面积为 A.13
A.13
B.14
C.15
D.16
E.17答案:E解析:
-
第21题:
如,在直角三角形ABC中,AC=4,BC=3,DE//BC,已知梯形BCDE的面积为3,则DE长为( )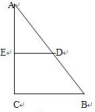
 答案:D解析:
答案:D解析:
-
第22题:
如图4,在等腰直角△ABC中,∠B=90o,将△ABC绕顶点A逆时针旋转60o后得到△ADE,则∠BAE=__________度。 答案:解析:105
答案:解析:105 -
第23题:
已知管线的截面半径r=10cm,圆的面积公式是:S=πr2,π=3.14则管线截面积是()cm2。
- A、213
- B、121
- C、314
- D、324
正确答案:C
