一个长方体的长、宽、高的和等于12，则这个长方体体积的最大值是（ ）。 A．60 B．64 C．68 D．72

题目

一个长方体的长、宽、高的和等于12，则这个长方体体积的最大值是（ ）。 A．60 B．64 C．68 D．72

相似考题

1.长方体的体积等于长×宽×高。()此题为判断题(对，错)。

2.一个长方体的长、宽、高恰好是三个连续的自然数，并且它的体积数值等于它的所有棱长之和的2倍，那么这个长方体的表面积是( )。A.74 B.148 C.150 D154

3.一个长方体的长、宽、高恰好是三个连续的自然数，并且它的体积数值等于它的所有棱长之和的 2倍，那么这个长方体的表面积是多少?( )A．74B．148C．150D．154

4.一个长方体的长、宽、高恰好是三个连续的自然数，并且它的体积数值等于它的所有棱长之和的 2 倍，那么这个长方体的表面积多少？( )A.74B.148C.150D.154

更多“一个长方体的长、宽、高的和等于12,则这个长方体体积的最大值是( )。 A.60 B.64 C.68 D.72 ”相关问题

  • 第1题：

    一个长方体的长、宽、高恰好是三个连续的自然数，并且它的体积数值等于它的所有 棱长之和的2倍，那么这个长方体的表面积是多少?（ ） A．74 B．148 C．150 D．154


    正确答案：B
    本题属于几何问题。设宽为x，那么长为x+1，高为x-1，所有棱长之和为4×3x＝12x，体积为x(x+1)(x－1)，根据题意2×12x=x(x+1)(x－1)，解得x＝5。所以长为6，高为4。表面积＝2×(4×5+4×6+5×6)=148。故选B。

  • 第2题：

    —个长方体的长、宽、高的和等于12,则这个长方体体积的最大值是（）。

    A.60
    B.64
    C.68
    D.72

    答案：B
    解析：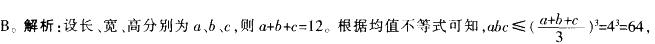

    即当a=b=c=4时，长方形体积最大，为64。

  • 第3题：

    一个长方体的长、宽、高恰好是三个连续的自然数，并且它的体积数值等于它的所有棱长之和的2倍，那么这个长方体的表面积是( )。


    A. 74
    B. 148
    C. 150
    D. 154

    答案：B
    解析：
    解题指导： 设该长方体的长、宽、高分别是x一1，X，X十l。那么有，(x一1)x(x+1)=2×4 F-(x—1)+x+(x+1)]，解得x＝5。所以这个长方体的表面积为：(4×5+4×6+5×6)×2=148.故答案为B。

  • 第4题：

    一个长方体前面和上面的面积和是209平方厘米。如果这个长方体的长、宽、高都是以厘米为单位的质数，那么这个长方体的体积是多少立方厘米?

    A．209

    B．342

    C．374

    D．418


    正确答案：
    设长、宽、高分别为x、y、z厘米，则x(y+z)=209=11×19。
    由于11和19都是奇数。说明y和z之间必然有一个偶数，而y、z都是质数，故其中一个数是2，不妨设z=2。若y+z=11，则y=9，不为质数，矛盾。因此，y+z=19，y=17，x=11。
    该长方体体积为11×17×2=374立方厘米。

  • 第5题：

    长方体棱长的和是48，其长、宽、高之比为3：2：1，则长方体的体积是：

    A.46
    B.386
    C.384
    D.48

    答案：D
    解析：
    设长宽高分别是3x,2x,x可得（3x+2x+x)x4=48，解得x=2。则长宽高分别是6，4，2,长方体体积为6x4x2=48。

相关内容