在具有6个顶点的无向简单图中,当边数最少为(26)条时,才能确保该图一定是连通图,当边数最少为(27)条时,才能确保该图一定是哈密尔顿图。给定带权的有向图,如下图所示。设该图代表一个地区的交通图,从S到T的最短路径有(28)条,路径的长度是(29),从S出发经过每点一次且只有一次到T的路径(哈密尔顿路径)有(30)条。A.11B.12C.13D.55
题目
在具有6个顶点的无向简单图中,当边数最少为(26)条时,才能确保该图一定是连通图,当边数最少为(27)条时,才能确保该图一定是哈密尔顿图。
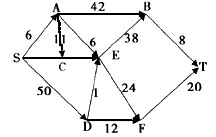
给定带权的有向图,如下图所示。设该图代表一个地区的交通图,从S到T的最短路径有(28)条,路径的长度是(29),从S出发经过每点一次且只有一次到T的路径(哈密尔顿路径)有(30)条。
A.11
B.12
C.13
D.55
相似考题
参考答案和解析
正确答案:A
更多“ 在具有6个顶点的无向简单图中,当边数最少为(26)条时,才能确保该图一定是连通图,当边数最少为(27)条时,才能确保该图一定是哈密尔顿图。给定带权的有向图,如下图所示。设该图代表一个地区的交通图,从S到T的最短路”相关问题
-
第1题:
n个结点的无向图,若没有顶点到自身的边,也没有一个顶点到另一个顶点的多重边,此时若有n(n-1)/2条边 ,则该无向图一定是连通图。
√ -
第2题:
n个结点的无向图,若不允许顶点到自身的边,也不允许出现顶点到顶点的多重边,且边的总和为n(n-1)/2 ,则该无向图一定是连通图。
n*(n-1)/2 -
第3题:
n个顶点的无向图,若没有顶点到自身的边,也没有一个顶点到另一个顶点的多重边,此时若有n(n-1)/2条边 ,则该无向图一定是连通图。
n*(n-1)/2 -
第4题:
具有6个顶点的无向图至少应有()条边才能确保是一个连通图。 A.5 B.6 C.7 D.8
A -
第5题:
21、具有6个顶点的无向图至少应有6条边才能确保是一个连通图。
选 A 。有 n 个顶点的连通图,至少需要 n-1 条边才能保持图的连通。多一条将形成回路,少一条将变成非连通图。当 n = 6 时, n-1 = 5 。
