某二叉树结点的前序序列为F，C，A，D，B，E，G，H，P，对称序序列为A，C，B，D，F，E， H，G，P，则该二叉树对应的后序序列为A．A，B，D，C，H，P，F，E，GB．A，B，D，C，H，P，G，E，FC．A，B，H，D，C，P，G，E，FD．A，D，C，H，B，P，G，E，F

题目

某二叉树结点的前序序列为F，C，A，D，B，E，G，H，P，对称序序列为A，C，B，D，F，E， H，G，P，则该二叉树对应的后序序列为

A．A，B，D，C，H，P，F，E，G

B．A，B，D，C，H，P，G，E，F

C．A，B，H，D，C，P，G，E，F

D．A，D，C，H，B，P，G，E，F

相似考题

1.（ 4 ）一棵二叉树结点的前序序列为 A 、 B 、 D 、 E 、 G 、 C 、 F 、 H 、 I ，对称序序列为 D 、 B 、G 、 E 、 A 、 C 、 H 、F 、 I ，则该二叉树结点的后序序列为 【 4 】 。

2.已知一棵二叉树前序序列和中序序列分别为A，B，D，E，G，C，F，H和D，B，G，E，A，C，H，F，则该二叉树的后序序列为______。

3.某二叉树的后序序列为B，D，C，A，F，G，E，对称序序列为A，B，C，D，E，F，G，则该二叉树的前序序列为( )。A．E，G，F，A，C，D，BB．E，A，C，B，D，G，FC．E，A，G，C，F，B，DD．E，G，A，C，D，F，B

4.（ 15 ）下列关于二叉树周游的叙述中，哪一项是正确的？A ）若一个结点是某二叉树对称序的最后一个结点，则它必是该二叉树前序的最后一个结点B ）若一个结点是某二叉树前序的最后一个结点，则它必是该二叉树对称序的最后一个结点C ）若一个树叶是某二叉树对称序的最后一个结点，则它必是该二叉树前序的最后一个结点D ）若一个树叶是某二叉树前序的最后一个结点，则它必是该二叉树对称序的最后一个结点

更多“某二叉树结点的前序序列为F,C,A,D,B,E,G,H,P,对称序序列为A,C,B,D,F,E, H,G,P,则该二叉树对应的 ”相关问题

  • 第1题：

    某二叉树的前序序列为ABCDEFG，中序序列为DCBAEFG，则该二叉树的深度(根结点在第1层)为()。

    A.2

    B.3

    C.4

    D.5


    正确答案：C

  • 第2题：

    某二叉树结点的中序序列为A、B、C、D、E、F、G，后序序列为B、D、C、A、F、G、E，该二叉树对应的层次遍历序列为()

    A.E、G、F、A、C、D、B

    B.E、A、C、B、D、G、F

    C.E、A、G、C、F、B、D

    D.E、G、A、C、D、F、B


    正确答案：C

  • 第3题：

    已知某二叉树的前序遍历序列为:C,B,F,E,G,A,D,H,I,J;中序遍历序列为:F,B,G,E,C,H,D,I,J,A;该二叉树的后序遍历序列为:()。


    参考答案：F,G,E,B,H,J,I,D,A,C

  • 第4题：

    某二叉树中序序列为A,B,C,D,E,F,G,后序序列为B,D,C,A,F,G,E则该二叉树对应的森林包括的树的棵树是()

    A、1

    B、2

    C、3

    D、概念上是错误的


    参考答案：B

  • 第5题：

    某二叉树结点的对称序序列为A、B、C、D、E、F、G，后序序列为B、D、C、A、F、G、E，则该二叉树对应的树林中高度最大的树的高度为 【】


    正确答案：2
    由后序序列可以看出，E为根结点，A,B,C,D为左子树结点，F,G为右子树结点

  • 第6题：

    第12和13题基于下面的叙述：

    某二叉树结点的前序序列为A、B、D、C、E、F，对称序序列为D、B、A、E、C、F。

    该二叉树结点的后序序列为（ ）。A．B、D、C、A、F、E B．B、D、C、F、A、EC．E、F、A、C、D、B D．D、B、E、F、C、A


    正确答案：D
    由前序序列，我们知道A为根节点，所以在后序序列中应该排在最后。

  • 第7题：

    下列问题基于下面的叙述；某二叉树节点的前序序列为E、A、C、B、D、G、F，对称序序列为A、B、C、D、E、F、G。

    该二叉树节点的后序序列为______。

    A．B、D、C、A、F、G、E

    B．B、D、C、F、A、G、E

    C．E、G、F、A、C、D、B

    D．E、G、A、C、D、F、B


    正确答案：A

  • 第8题：

    某二叉树结点的前序序列为E、A、C、B、D、G、F，对称序序列为A、B、C、D、E、F、 G，则该二叉树结点的后序序列为( )。

    A．B、D、C、A、F、G、E

    B．B、D、C、F、A、G、E

    C．E、G、F、A、C、D、B

    D．E、G、A、C、D、F、B


    正确答案：A
    解析：根据前序序列可知到E为根结点，所以后序序列中E必为最后一个元素，A，B， C，D为E的左子树对称序列，F，G是在E的右子树上的对称序列，再分析可知A是E的左子树的根，G是E的右子树的根，C是A的右子结点，B，D分别是C的左右子结点，F是G的左子结点。

  • 第9题：

    某二叉树的先序遍历(根、左、右)序列为 EFHIGJK 、中序遍历(左、根、右)序列为HFIEJKG, 则该二叉树根结点的左孩子结点和右孩子结点分别是（ ）。

    A.A,I.KB.F,IC.F,GD.I,G


    正确答案：C

  • 第10题：

    下列各题基于下面的叙述：某二叉树节点的对称序序列为A、B、C、D、E、P、G，后序序列为B、D、C、A、F、G、E。

    该二叉树节点的先序序列为 ______。

    A．E、G、F、A、C、D、B

    B．E、A、C、B、D、G、F

    C．E、A、G、C、F、B、D

    D．E、G、A、C、D、F、B


    正确答案：B

  • 第11题：

    某二叉树的先序遍历(根、左、右)序列为 EFHIGJK 、中序遍历(左、根、右)序列为 HFIEJKG, 则该二叉树根结点的左孩子结点和右孩子结点分别是（37）

    A.A,I.K
    B. F,I
    C. F,G
    D.I,G

    答案：C
    解析：
    由先序遍历看，E为根节点，F为根节点的作孩子。在看中序遍历，则左树有：IE两个子结点。那么E的右孩子结点为G。

  • 第12题：

    某二叉树的先序遍历序列为c a b f e d g,中序遍历序列为a b c d e f g,则该二叉树是（ ）。

    A.完全二叉树
    B.最优二叉树
    C.平衡二叉树
    D.满二叉树

    答案：C
    解析：
    本题考查数据结构基础知识。二叉树的遍历主要有四种：前序遍历（先根遍历、先序遍历）：遵循“根-左-右”的递归遍历思想，根一定是当前子二叉树先序遍历序列的第一个元素；中序遍历（中根遍历）：遵循“左-根-右”的递归遍历思想，根位于是当前子二叉树中序遍历序列的中部位置，左边是当前根的左二叉树，右边是当前根的右二叉树；后序遍历（后根遍历）：遵循“左-右-根”的递归遍历思想，根一定是遍历序列的最后一个元素；层次遍历：遵循从上到下，直左而右的遍历思想，根一定是遍历序列的第一个元素。根据题意，本二叉树为：



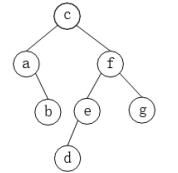
    平衡二叉树或者是一棵空树，或者是具有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。本题的二叉树满足平衡二叉树的特点要求，故本题选择C选项

  • 第13题：

    一棵二叉树结点的前序序列为A、B、D、E、G、C、F、H、I，对称序序列为D、B、G、E、A、C、H、F、I，则该二叉树结点的后序序列为________。


    正确答案：
    D、G、E、B、H、I、F、C、A。
    根据前序序列以及对称序序列的结果还原得到如下的二叉树：

    所以该二叉树的后序序列为D、G、E、B、H、I、F、C、A。

  • 第14题：

    某二叉树结点的前序序列为E、A、C、B、D、G、F，对称序列为A、B、C、D、E、F、G。该二叉树结点的后序序列为()

    A.B、C、F、G、E

    B.C、F、A、G、E

    C.E、G、F、A、B

    D.E、G、A、C、F、B


    正确答案：A

  • 第15题：

    某二叉树结点的对称序序列为A、B、C、D、E、F、G，后序序列为B、D、C、A、F、G、E。则该二叉树对应的树林包括【 】棵树。


    正确答案：2
    2 解析：本题考核有关树、二叉树和二叉树周游的基本知识，参考2.4“树形结构”一节。

  • 第16题：

    某二叉树结点的前序序列为A、B、D、E、G、C、F、H、I，对称序序列为D、B、G、 E、A、C、H、F、I，则该二叉树结点的后序序列为【 】。


    正确答案：DGEBHIFCA
    D,G,E,B,H,I,F,C,A 解析：依据前序遍历序列可确定根结点为A；再依据对称序遍历序列可知其左子树由DBGE构成，右子树为 CFHI；又由左子树的前序遍历序列可知其根结点为B，由对称序遍历序列可知其左子树为D，右子树由EG构成。以此类推，此二叉树为：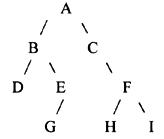

    根据后序遍历的定义，求得该二叉树的后序遍历序列为：D,G,E,B,H,I,F,C,A。

  • 第17题：

    二叉树的前序遍历序列为A，B，D，C，E，P，G，中序遍历序列为D，B，C，A，F，E,G，其后序遍历序列为(44)。

    A．D，C，F，G,E,B,A

    B．D，C，B，P，G,E,A

    C．F，G,E,D,C,B,A

    D．D，C，F，G,B,E,A


    正确答案：B
    解析：根据二叉树的前序序列和中序序列可以唯一地恢复二叉树，原则是：在前序序列中确定根结点，到中序序列中分出根结点的左、右子树。因此本题先根据前序序列和中序序列将二叉树，恢复出来，然后对二叉树进行后序遍历，即可得到后序序列，具体由前序序列“ABDCEFG”可以确定树根结点A，在中序序列中以A为界，“DBC”是其左子树中结点，“FEG”是其右子树中结点；接下来，由前序序列确定每棵子树的根，再在中序序列中分出其左右子树中的节点……故本题选B。

  • 第18题：

    下列问题是基于下面的叙述：某二叉树结点的前序序列为E、A、C、B、D、C、F，对称序序列为A、B、C、D、E、F、C。

    该二叉树结点的后序序列为

    A．B、D、C、A、F、C、E

    B．B、D、C、F、A、C、E

    C．E、C、F、A、C、D、B

    D．E、C、A、C、D、F、B


    正确答案：A
    解析：二叉树是树形结构的一种重要类型，它是结点的有限集合，这个有限集合或者为空集，或者有一个根(N)结点及两个不相交的、分别称作这个根的左子树(L)和右于树(R)的二叉树组成。按周游二叉树的方式可以分为：前序序列法(NLR)：访问根，按前序周游左予树，按前序周游右子树；后序序列法(LRN)：按后序周游左子树，按后序周游右子树，访问根；对称序列法(LNR)：按对称序周游左子树，访问根，按对称序周游右子树。由题意“某二叉树结点的前序序列为E、A、C、B、D、C、F，对称序序列为A、B、C、D、E、F、C”，按照各种周游顺序的定义可以得到二叉树的树形结构，如图1所示。所以该二叉树的后序序列为B、D、C、A、F、C、K。

  • 第19题：

    某二叉树结点的前序序列为F,C,A,D,B,E,G,H,P，对称序序列为A,C,B,D,F,E,H,G,P，则该二叉树对应的后序序列为 ______。

    A．A,B,D,C,H,P,F,E,G

    B．A,B,D,C,H,P,G,E,F

    C．A,B,H,D,C,P,G,E,F

    D．A,D,C,H,B,P,G,E,F


    正确答案：B
    解析：二叉树的遍历可以分为三种：前序遍历、中序遍历、后序遍历。依据前序遍历序列可确定根结点为F；再依据中序遍历序列可知其左子树由ACBD构成，右子树为EHGP；又由左子树的前序遍历序列可知其根结点为C，由中序遍历序列可知其左子树为A，右子树由BD构成。以此类推，此二叉树为：根据前序遍历的定义，求得该二叉树的后序遍历序列为：A,B,D,C,H,P,G,E,F。

  • 第20题：

    第(11)至(12)题基于下面的叙述：某二叉树结点的前序序列为E、A、C、B、D、G、F，对称序序列为A、B、C、D、E、F、G。 该二叉树结点的后序序列为

    A．B、D、C、A、F、G、E

    B．B、D、C、F、A、G、E

    C．E、G、F、A、C、D、B

    D．E、G、A、C、D、F、B


    正确答案：A
    解析：由二叉树前序及对称序画出二叉树。

  • 第21题：

    若某二叉树采用广义表(A(B(E)，C(F(H，G)，D)))表示，该二叉树的中序遍历序列为(47)。

    A．A，B，E，C，F，H，G，D

    B．E，B，H，G，F，D，C，A

    C．E，B，A，H，F，G，C，D

    E．D


    正确答案：C
    解析：首先根据二叉树的广义表表示将该二叉树恢复，然后对二叉树进行中序遍历即可得到二叉树的中序序列为C。

  • 第22题：

    二叉树的前序遍历序列为A，B，D，C，E，P，G，中序遍历序列为D，B，C，A，F，E，G，其后序遍历序列为(41)。

    A．D，C，F，G，E，B，A

    B．D，C，B，P，G，E，A

    C．F，G，E，D，C，B，A

    D．D，C，P，G，B，E，A


    正确答案：B
    解析：根据二叉树的前序序列和中序序列可以惟一地恢复二叉树，原则是：在前序序列中确定根结点，到中序序列中分出根结点的左、右子树。因此本题先根据前序序列和中序序列将二叉树恢复出来，然后对二叉树进行后序遍历，即可得到后序序列，故本题选B。

  • 第23题：

    某二叉树中序序列为A，B，C，D，E，F，G，后序序列为B，D，C，A，F，G，E，则前序序列是()。

    A.E，G，F，A，C，D，B
    B.E，A，
    C.B，D，G，F
    D.以上都不对

    答案：B
    解析：
    由后序序列知E为根节点，再由中序序列知A，B，C，D为E的左子树1，F，G，E为右子树1；由后序序列知A为左子树l的根节点，B，C，D为A的右子树2。依次类推可得到该数，其前序序列也可自然而然的得到。

  • 第24题：

    单选题
    某二叉树结点的中序序列为A、B、C、D、E、F、G，后序序列为B、D、C、A、F、G、E，则其左子树中结点数目为（）
    A

    3

    B

    2

    C

    4

    D

    5


    正确答案： D
    解析： 暂无解析

相关内容