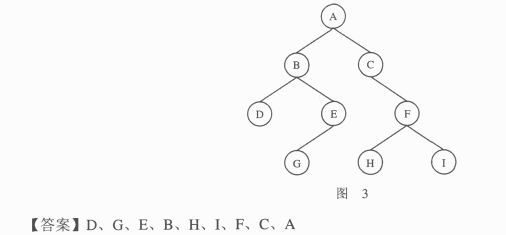
( 4 )一棵二叉树结点的前序序列为 A 、 B 、 D 、 E 、 G 、 C 、 F 、 H 、 I ,对称序序列为 D 、 B 、G 、 E 、 A 、 C 、 H 、F 、 I ,则该二叉树结点的后序序列为 【 4 】 。
题目
( 4 )一棵二叉树结点的前序序列为 A 、 B 、 D 、 E 、 G 、 C 、 F 、 H 、 I ,对称序序列为 D 、 B 、G 、 E 、 A 、 C 、 H 、F 、 I ,则该二叉树结点的后序序列为 【 4 】 。
相似考题
参考答案和解析

更多“( 4 )一棵二叉树结点的前序序列为 A 、 B 、 D 、 E 、 G 、 C 、 F 、 H 、 I ,对称序序列为 D 、 B 、G 、 ”相关问题
-
第1题:
某二叉树结点的前序序列为F,C,A,D,B,E,G,H,P,对称序序列为A,C,B,D,F,E,H,G,P,则该二叉树对应的后序序列为 ______。
A.A,B,D,C,H,P,F,E,G
B.A,B,D,C,H,P,G,E,F
C.A,B,H,D,C,P,G,E,F
D.A,D,C,H,B,P,G,E,F
正确答案:B
解析:二叉树的遍历可以分为三种:前序遍历、中序遍历、后序遍历。依据前序遍历序列可确定根结点为F;再依据中序遍历序列可知其左子树由ACBD构成,右子树为EHGP;又由左子树的前序遍历序列可知其根结点为C,由中序遍历序列可知其左子树为A,右子树由BD构成。以此类推,此二叉树为:根据前序遍历的定义,求得该二叉树的后序遍历序列为:A,B,D,C,H,P,G,E,F。 -
第2题:
第(11)至(12)题基于下面的叙述:某二叉树结点的前序序列为E、A、C、B、D、G、F,对称序序列为A、B、C、D、E、F、G。 该二叉树结点的后序序列为
A.B、D、C、A、F、G、E
B.B、D、C、F、A、G、E
C.E、G、F、A、C、D、B
D.E、G、A、C、D、F、B
正确答案:A
解析:由二叉树前序及对称序画出二叉树。 -
第3题:
下列问题是基于下面的叙述:某二叉树结点的前序序列为E、A、C、B、D、G、F,对称序序列为A、B、C、D、E、 F、G。
该二叉树结点的后序序列为
A.B、D、C、A、F、G、E
B.B、D、C、F、A、G、E
C.E、G、F、A、C、D、B
D.E、G、A、C、D、F、B
正确答案:A
解析:二叉树是树形结构的一种重要类型,它是结点的有限集合,这个有限集合或者为空集,或者有一个根(N)结点及两个不相交的、分别称作这个根的左子树(L)和右子树(R)的二叉树组成。按周游二叉树的方法可以分为:前序序列法(NLR):访问根,按前序周游左子树,按前序周游右子树;后序序列法(LRN):按后序周游左子树,按后序周游右子树,访问根;对称序列法(LNR):按对称序周游左子树,访问根,按对称序周游右子树。由题意“某二叉树结点的前序序列为E、A、C、B、D、G、F,对称序序列为A、B、C、D、E、F、G”,按照各种周游顺序的定义可以得到二叉树的树形结构,如图所示。所以该二叉树的后序序列为B、D、C、A、F、G、E,本题正确答案为选项A。 -
第4题:
某二叉树结点的前序序列为E、A、C、B、D、G、F,对称序序列为A、B、C、D、E、F、 G,则该二叉树结点的后序序列为( )。
A.B、D、C、A、F、G、E
B.B、D、C、F、A、G、E
C.E、G、F、A、C、D、B
D.E、G、A、C、D、F、B
正确答案:A
解析:根据前序序列可知到E为根结点,所以后序序列中E必为最后一个元素,A,B, C,D为E的左子树对称序列,F,G是在E的右子树上的对称序列,再分析可知A是E的左子树的根,G是E的右子树的根,C是A的右子结点,B,D分别是C的左右子结点,F是G的左子结点。 -
第5题:
某二叉树结点的前序序列为F,C,A,D,B,E,G,H,P,对称序序列为A,C,B,D,F,E, H,G,P,则该二叉树对应的后序序列为
A.A,B,D,C,H,P,F,E,G
B.A,B,D,C,H,P,G,E,F
C.A,B,H,D,C,P,G,E,F
D.A,D,C,H,B,P,G,E,F
正确答案:B
解析:二叉树的遍历可以分为三种:前序遍历、中序遍历、后序遍历。依据前序遍历序列可确定根结点为F5再依据中序遇历序列可知其左子树由ACBD构成,右子树为EHGP;又由左子树的前序遍历序列可知其根结点为C,由中序遍历序列可知其左子树为A,右子树由BD构成。以此类推,此二叉树为:根据前序遍历的定义,求得该二叉树的后序遍历序列为:A,B,D,C,H,P,G,E,F。
