定义了一个“f = lambda x : x**2+5*x+1 ”,则f(4)= 。
题目
定义了一个“f = lambda x : x**2+5*x+1 ”,则f(4)= 。
相似考题
更多“定义了一个“f = lambda x : x**2+5*x+1 ”,则f(4)= 。”相关问题
-
第1题:
设函数f(x)=1/x+1,则f(f(x))=()。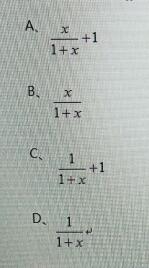
答案:A
解析:由函数f(x)=1/x+1,
令f(x)=t
则f(f(x))=f(t)=1/t+1=1/(1/x+1)+1=x/(1+x)+1,故选A。
-
第2题:
以下if语句书写正确的是( )
A.if(x=0;) printf("%f",x); elseprintf("%f",-x);
B.if(x>0) {x=x+1;printf("%f",x);} else printf("%f",-x);
C.if(x>0); {x=x+1;printf("%f",x);} else printf("%f",-x);
D.if(x>0) {x=x+1;printf("%f",x)} else printf("%f",-x);
正确答案:B
-
第3题:
已知f(x+1)=-1/f(x),若f(2)=2007,则f(2007)=( )
A. 2
B. -1/2007
C. 1/2007
D. 2008答案:B解析:解题指导: 由题意可得:X为奇数时f(x)=-1/2007,,X为偶数时f(x)=2007,故答案为B。 -
第4题:
若f(x+1)=x2-2x+3,则f(x)=( )A.x2+2x+6
B.x2+4x+6
C.x2-2x+6
D.x2-4x+6答案:D解析:f(x+1)=x2-2x+3=(x+1)2-4(x+1)+6,∴f(x)=x2-4x+6.(答案为D) -
第5题:
设f(x-1)=x2,则f(x+1)=()
正确答案:x2+4x+4 -
第6题:
已知f=lambda x:5,那么表达式f(3)的值为()。
正确答案:5 -
第7题:
已知f=lambda x:x+5,那么表达式f(3)的值为()。
正确答案:8 -
第8题:
单选题设y=f[(2x-1)/(x+1)],f′(x)=ln(x1/3),则dy/dx( )。Aln[(2x-1)/(x+1)](x+1)
Bln[(2x-1)/(x+1)]/(x+1)2
Cln[(2x-1)/(x+1)](x+1)2
Dln[(2x-1)/(x+1)]/(x+1)
正确答案: D解析:
令u=(2x-1)/(x+1),则u′(x)=3/(x+1)2。dy/dx=f′(u)·u′(x)=ln(u1/3)·3/(x+1)2=ln[(2x-1)/(x+1)]/(x+1)2。 -
第9题:
单选题F[x]中,若f(x)+g(x)=1,则f(x+1)+g(x+1)=()。A0.0
B1.0
C2.0
D3.0
正确答案: C解析: 暂无解析 -
第10题:
填空题设f(x)是可导函数,且f′(x)=sin2[sin(x+1)],f(0)=4,f(x)的反函数是x=φ(y),则φ′(4)=____。正确答案: 1/sin2(sin1)解析:
φ′(4)=1/f′(0)=1/sin2(sin1)。 -
第11题:
问答题下面三种表示方法有什么不同的含义? (1)f=3*x^2+5*x+2 (2)f='3*x^2+5*x+2' (3)x=sym('x') f=3*x^2+5*x+2正确答案: (1)f=3*x^2+5*x+2
表示在给定x时,将3*x^2+5*x+2的数值运算结果赋值给变量f,如果没有给定x则指示错误信息。
(2)f='3*x^2+5*x+2'
表示将字符串'3*x^2+5*x+2'赋值给字符变量f,没有任何计算含义,因此也不对字符串中的内容做任何分析。
(3)x=sym('x')
f=3*x^2+5*x+2
表示x是一个符号变量,因此算式f=3*x^2+5*x+2就具有了符号函数的意义,f也自然成为符号变量了。解析: 暂无解析 -
第12题:
填空题已知f=lambda x:x+5,那么表达式f(3)的值为()。正确答案: 8解析: 暂无解析 -
第13题:
设f(x)=x(x+1)(x+2)(x+3),则f'(x)=0的正根的个数为()A、0
B、1
C、2
D、3
答案:A
解析:f(x)=x(x+1)(x+2)(x+3)=x^4+6x^3+11x^2+6x,所以f'(x)=4x^3+18x^2+22x+6,因为求f'(x)=0的正根,即x>0,所以当x>0时,f'(x)=4x^3+18x^2+22x+6>0,所以f'(x)=0没有正根。故选A。
-
第14题:
设f(x-1) =x2,则f(x+1)等于:
A. (x-2)2 B. (x+2)2 C. x2-22 D.x2+22答案:B解析:提示:设x-1=t,则x=t+1,代入函数表达式,得f(t)= (t+1)2,即f(x) = f(x+1)2,从而求得f(x+1)的表达式。 -
第15题:
设f(x)在x=a的某个邻域内有定义,则f(x)在x-a处可导的一个充分条件是( )。
 答案:D解析:用可导的定义判断
答案:D解析:用可导的定义判断 -
第16题:
设f(x)=x3+4x2+11x+7,则f(x+1)= ()A.x3+7x2+22x+23
B.x3—7x2+22x+23
C.x3+7x2—22x+23
D.x3—7x2—22x+23答案:A解析: -
第17题:
下面三种表示方法有什么不同的含义? (1)f=3*x^2+5*x+2 (2)f='3*x^2+5*x+2' (3)x=sym('x') f=3*x^2+5*x+2
正确答案: (1)f=3*x^2+5*x+2
表示在给定x时,将3*x^2+5*x+2的数值运算结果赋值给变量f,如果没有给定x则指示错误信息。
(2)f='3*x^2+5*x+2'
表示将字符串'3*x^2+5*x+2'赋值给字符变量f,没有任何计算含义,因此也不对字符串中的内容做任何分析。
(3)x=sym('x')
f=3*x^2+5*x+2
表示x是一个符号变量,因此算式f=3*x^2+5*x+2就具有了符号函数的意义,f也自然成为符号变量了。 -
第18题:
F[x]中,若f(x)+g(x)=1,则f(x+1)+g(x+1)=()。
- A、0.0
- B、1.0
- C、2.0
- D、3.0
正确答案:B -
第19题:
单选题设y=f[(2x-1)/(x+1)],f′(x)=ln(x1/3),则dy/dx=( )。Aln[(2x-1)/(x-1)]/(x+1)2
Bln[(2x+1)/(x+1)]/(x+1)2
Cln[(2x+1)/(x+1)]/(x-1)2
Dln[(2x-1)/(x+1)]/(x+1)2
正确答案: D解析:
令u=(2x-1)/(x+1),则u′(x)=3/(x+1)2。dy/dx=f′(u)·u′(x)=ln(u1/3)·3/(x+1)2=ln[(2x-1)/(x+1)]/(x+1)2。 -
第20题:
单选题若函数z=f(x,y)满足∂2z/∂y2=2,且f(x,1)=x+2,fy′(x,1)=x+1,则f(x,y)=( )。Ay2+(x-1)y+2
By2+(x+1)y+2
Cy2+(x-1)y-2
Dy2+(x+1)y-2
正确答案: D解析:
因为∂2z/∂y2=2,等式两边对y积分得,fy′(x,y)=2y+φ1(x)。
又fy′(x,1)=x+1,则φ1(x)=x-1。
故fy′(x,y)=2y+x-1。两边再对y积分得f(x,y)=y2+xy-y+φ2(x)。
又f(x,1)=x+2,故φ2(x)=2。
故f(x,y)=y2+xy-y+2。 -
第21题:
填空题设f(x-1)=x2,则f(x+1)=()正确答案: x2+4x+4解析: 暂无解析 -
第22题:
填空题设y=f[(2x-1)/(x+1)],f′(x)=ln(x1/3),则dy/dx____。正确答案: ln[(2x-1)/(x+1)]/(x+1)2解析:
令u=(2x-1)/(x+1),则u′(x)=3/(x+1)2。dy/dx=f′(u)·u′(x)=ln(u1/3)·3/(x+1)2=ln[(2x-1)/(x+1)]/(x+1)2。 -
第23题:
单选题设f(x)是可导函数,且f′(x)=sin2[sin(x+1)],f(0)=4,f(x)的反函数是x=φ(y),则φ′(4)=( )。Asin2(sin1)
B1/sin2(sin1)
Csin(sin1)
D1/sin(sin1)
正确答案: D解析:
φ′(4)=1/f′(0)=1/sin2(sin1)。 -
第24题:
单选题设f(x)是可导函数,且f′(x)=sin2[sin(x+1)],f(0)=4,f(x)的反函数是x=φ(y),则φ′(4)=( )。A1/sin2(sin1)
Bsin2(sin1)
C-sin2(sin1)
D-1/sin2(sin1)
正确答案: B解析:
φ′(4)=1/f′(0)=1/sin2(sin1)。
